java实现组合数_n！_杨辉三角_组合数递推公式_回文数_汉诺塔问题

一，使用计算机计算组合数

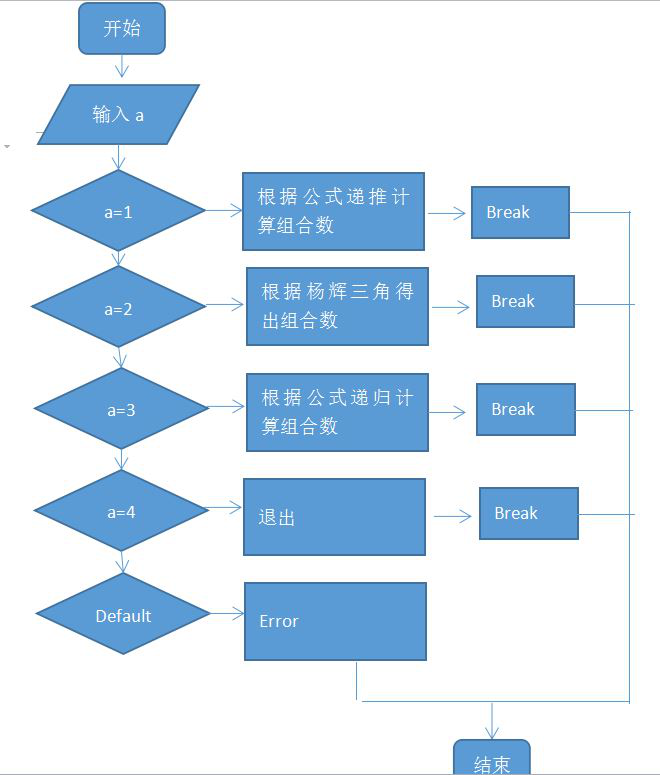
1，设计思想

（1）使用组合数公式利用n！来计算Cn^k=n!/k!(n-k)!用递推计算阶乘

（2）使用递推的方法用杨辉三角计算Cn+1^k=Cn^k-1+Cn^k

通过数组写出杨辉三角，对应的几排几列就对应这组合数的n和k

（3）使用递归的方法用组合数递推公式计算

定义带参数的方法，将不同的参数传递给方法，然后计算出阶乘

2，程序流程图

3，程序源代码

package 计算组合数;

import java.util.Scanner;

public class Caculate {

int n,k;//定义私有成员变量

static Scanner input=new Scanner(System.in);

public void caculate1(){

System.out.println("请输入n和k的值");

System.out.print("n:");

n=input.nextInt();

System.out.print("k:");

k=input.nextInt();

if(k>n)

System.out.println("k不能大于n");

else if(k==n)

System.out.println(1);//规定当n=k时 输出1

else{

int a=1,b=1,c=1;//初始化a b c为1

int d=n-k;

while(k!=0||d!=0){//当k和n-k都等于0时循环结束

if(n!=0){

a=a*n;//递推

n=n-1;

}

if(k!=0){

b=b*k;//递推

k=k-1;

}

if(d!=0){

c=c*d;//递推

d=d-1;

}

}

int result=a/(b*c);

System.out.println("Cn^k="+result);

}

}

public void caculate2(){

int a[][]=new int [100][100];

for(n=0;n<10;n++){

a[n][0]=1;

for(k=0;k<=n;k++){

if(n==k)a[n][k]=1;

if(n>k&&k!=0)

a[n][k]=a[n-1][k-1]+a[n-1][k];

System.out.print(a[n][k]+" ");

}

System.out.print("\n");

}

System.out.println("计算组合数\n请输入n和k的值：");

n=input.nextInt();

k=input.nextInt();

System.out.println("由杨辉三角可得知C(n+1)^k的值为："+a[n+1][k]);

System.out.println("由杨辉三角可得知Cn^(k-1)的值为："+a[n][k-1]);

System.out.println("由杨辉三角可得知Cn^k的值为："+a[n][k]);

System.out.println("所以得出:\nC(n+1)^k=Cn^(k-1)+Cn^k");

}

public int caculate3(int n){

if(n==0)

System.exit(0);

if(n==1)

return 1;

else

return n*caculate3(n-1);              //递归

}

public static void main(String[] args){

int a;

do{

System.out.println("1，使用组合数公式利用n！来计算Cn^k=n!/k!(n-k)!");

System.out.println("2，使用递推的方法用杨辉三角计算Cn+1^k=Cn^k-1+Cn^k");

System.out.println("3，使用递归的方法用组合数递推公式计算");

System.out.println("4，退出");

a=input.nextInt();

Caculate Ca=new Caculate();

switch(a){

case 1:{Ca.caculate1();System.out.println();}break;

case 2:{Ca.caculate2();System.out.println();}break;

case 3:{

int a1=1,b1=1,c1=1,d1=1,e1=1,f1=1;

System.out.println("组合数递推公式为:Cn^k=C(n-1)^(k-1)+C(n-1)^k");

System.out.println("请输入n和k的值：");

System.out.print("n:");

int n1=input.nextInt();

System.out.print("k:");

int k1=input.nextInt();

//组合数递推公式计算

if(n1-1>=k1){

a1=Ca.caculate3(n1);     //计算n！

b1=Ca.caculate3(n1-1);   //计算（n-1）！

c1=Ca.caculate3(k1);     //计算k！

d1=Ca.caculate3(k1-1);   // 计算（k-1）！

e1=Ca.caculate3(n1-k1);   //计算（n-k）！

if(n1-1-k1>0)

f1=Ca.caculate3(n1-1-k1);  //计算（n-k-1）！

if(k1==0)

System.out.println("Cn^k="+1);

else

System.out.println("Cn^k="+a1/(c1*e1));

if(n1-1==k1-1||k1==1)

System.out.println("C(n-1)^(k-1)="+1);

else

System.out.println("C(n-1)^(k-1)="+b1/(d1*e1));

if(n1-1==k1||k1==0)

System.out.println("C(n-1)^k="+1);

else

System.out.println("C(n-1)^k="+b1/(c1*f1));

System.out.println("由上述结果可得知：Cn^k=C(n-1)^(k-1)+C(n-1)^k");

}

else

System.out.println("error! n不能小于k且n-1不能小于k");

System.out.println();

}break;

case 4:{System.exit(0);}break;

default:System.out.println("error");

}

}while(a!=4);

}

}

4，结果截图

二，汉诺塔问题

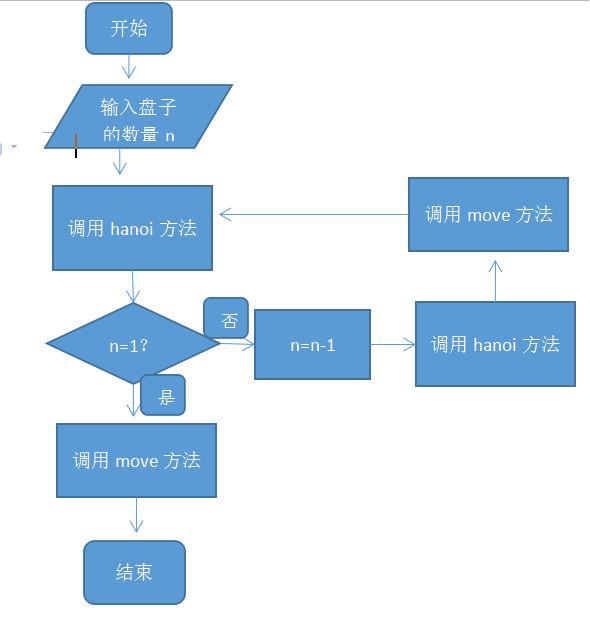
1，设计思想

定义hanio方法递归调用直到盘子数量等于1

2，程序流程图

3，程序源代码

package 汉诺塔问题;

import java.util.Scanner;

public class Ta {

public void hanoi(int n,char one,char two,char three){

if(n==1){

move(one,three);

}

else{

hanoi(n-1,one,three,two);

move(one,three);

hanoi(n-1,two,one,three);

}

}

public void move(char x,char y){

System.out.println(x+"->"+y);

}

public static void main(String[] args){

//int A[]=new int[64];

int number;

Scanner input=new Scanner(System.in);

System.out.print("请输入移动的盘子数量：");

number=input.nextInt();

System.out.println("假设有三个底座A、B、C，那么移动盘子的过程如下：");

Ta t=new Ta();

t.hanoi(number,'A','B','C');

}

}

4，结果截图

三，使用递归方式判断某个字符串是否回文

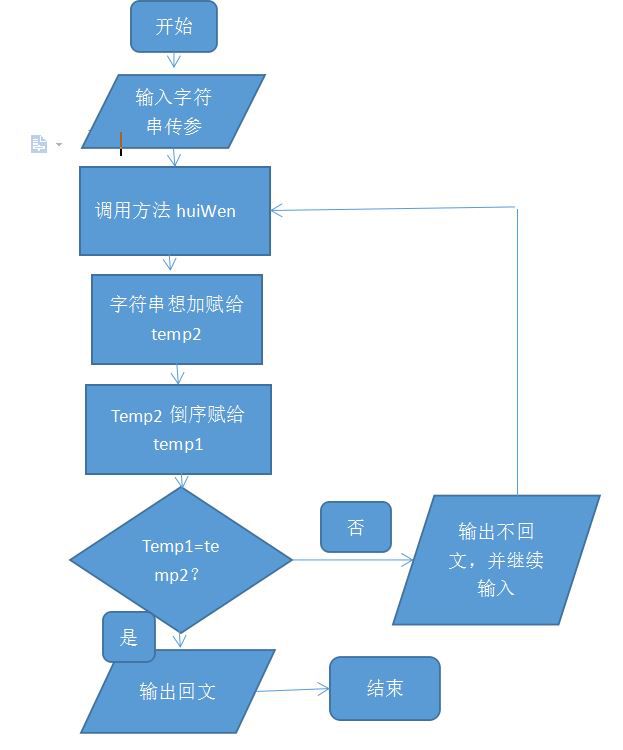
1，设计思想

（1）先输入一个字符串传参进入huiWen方法中

（2）将输入的字符串想加传给temp2

（3）将temp2倒序传给temp1

（4）判断：如果字符串temp1和temp2相同，则回文；否则输出不回文的字样并提示用户继续输入

（5）如果不是回文则调用方法自身继续输入字符串

2，程序流程图

3，程序源代码

package 递归判断字符串是否回文;

import java.util.Scanner;

public class Judge {

String temp2=" ",temp1;

Scanner input=new Scanner(System.in);

public void huiWen(String s1){

temp2=s1+temp2;

temp1=reverseString(temp2);   //调用reverse方法使字符串temp2倒序

if(temp2.equals(temp1)){

System.out.println("该字符串回文");

System.out.println("原字符串："+temp2);

System.out.println("现字符串："+temp1);

}

else{

if(!temp2.equals(temp1))

System.out.println("以上字符串不回文,请继续输入");

huiWen(input.nextLine());      //调用自身继续输入字符串

}

}

public static String reverseString(String string){   //使字符串倒序的方法

StringBuffer buf=new StringBuffer();

buf.append(string);

return buf.reverse().toString();

}

public static void main(String[] args){

Scanner input=new Scanner(System.in);

Judge j=new Judge();

System.out.println("请输入一个字符串,直到输入空格结束：");

j.huiWen(input.nextLine());

}

}

4，结果截图