3424:Candies（差分约束，Dijkstra）（配对堆优化

题面链接

题解

令x-y<=z表示x最大比y大z。 
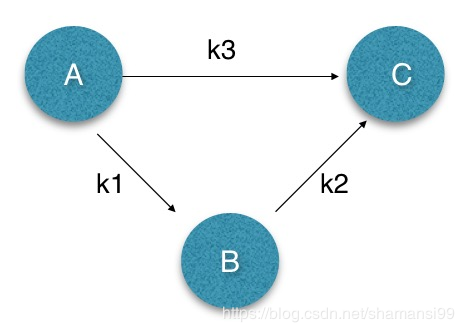
若b-a<=k1, c-b<=k2, c-a<=k3，那么c-a最大为多少呢？显然应该等于min(k1+k2, k3)。可以用下图来表示示(不擅图丑勿怪)

C++堆优化代码

//链式前向星存图+迪杰斯特拉堆优化
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int MAX=;
const int MAXN=;
const int INF=0x3f3f3f3f;
int head[MAX],cnt=;
int t,n,a,b,len;
int dist[MAX];
bool vis[MAX];
struct Edge{                            //链式前向星
    int next,val,to;
}Edge[MAXN];
inline void add(int u,int v,int w)
{
    Edge[cnt].to=v;
    Edge[cnt].val=w;
    Edge[cnt].next=head[u];
    head[u]=cnt++;
}
struct node
{
    int pos,dist;                        //点的位置及距离
    node(){}
    node(int p,int d)
    {
        pos=p;
        dist=d;
    }
    bool operator < (const node &rhs)const        //重载 <
    {
        return dist>rhs.dist;
    }
};
void Dij(int start)
{
    priority_queue<node>que;
    for(int i=;i<=t;i++)
    {
        dist[i]=INF;
        vis[i]=false;
    }
    dist[start]=;
    que.push(node(start,));

    while(!que.empty())
    {
        node temp=que.top();                //优先队列为首的元素及dist数组的最小值
        que.pop();
        int v=temp.pos;                        //筛选出最小值
        if(vis[v])continue;                    //判断是否已经找到最小值 ，是的话跳过
        vis[v]=true;

        for(int i=head[v];i!=-;i=Edge[i].next)        //用最小值的点为弧尾的边更新距离
        {
            int to=Edge[i].to;
            if(dist[to]>dist[v]+Edge[i].val)
            {
                dist[to]=dist[v]+Edge[i].val;
                que.push(node(to,dist[to]));
            }
        }
    }
}
int main()
{
    while(scanf("%d%d",&t,&n)!=EOF)
    {
        memset(head,-,sizeof(head));
        for(int i=;i<n;i++)
        {
            scanf("%d%d%d",&a,&b,&len);
            add(a,b,len);
            //add(b,a,len);
        }
        Dij();
        printf("%d\n",dist[t]);
    }
    return ;
}

C++配对堆优化

#include <bits/stdc++.h>
#include<ext/pb_ds/priority_queue.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef pair<int,int> pii;
typedef __gnu_pbds::priority_queue<pii,greater<pii>,pairing_heap_tag> Heap;
const int maxn=1e5+;
const int INF=0x3f3f3f3f;

int n,m,s;
struct Edge{
    int u,v,w;
    Edge(int _u=,int _v=,int _w=){u=_u,v=_v,w=_w;}
};
vector<Edge> E;
vector<int> G[maxn];
void addedge(int u,int v,int w)
{
    E.push_back(Edge(u,v,w));
    G[u].push_back(E.size()-);
}

int d[maxn];
void dijkstra()
{
    memset(d,0x3f,sizeof(d));

    Heap Q;
    Heap::point_iterator id[maxn];

    d[s]=;
    id[s]=Q.push(make_pair(d[s],s));
    while(!Q.empty())
    {
        int u=Q.top().second; Q.pop();
        for(int i=;i<G[u].size();i++)
        {
            Edge &e=E[G[u][i]]; int v=e.v;
            if(d[v]>d[u]+e.w)
            {
                d[v]=d[u]+e.w;
                if(id[v]!=) Q.modify(id[v],make_pair(d[v],v));
                else id[v]=Q.push(make_pair(d[v],v));
            }
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m)){
    s = ;//起点
    //memset(d,0,sizeof d);
    memset(G,,sizeof G);
    for(int i=;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w);
    }
    dijkstra();
    //for(int i=1;i<=n;i++) printf("%d%s",d[i],((i==n)?"\n":" "));
    printf("%d\n",d[n]);
    }
}