六一新玩法！AI涂鸦秒变精美艺术画

摘要：上华为云ModelArts体验AI涂鸦新玩法，赢漫威复仇者联盟乐高！祝大小朋友们六一儿童节快乐~

本文分享自华为云社区《【云享热点】六一新玩法！AI 涂鸦秒变精美艺术画》，作者：华为云社区精选。

又是一年儿童节，记得小时候的涂涂画画吗

现在有了 AI 这只 “魔法棒”，它们变成了这样

上传你的涂鸦线稿

只需简单几步就可以秒变精美艺术画！

大朋友可以找回童年涂鸦的乐趣

小朋友也能够体验妙笔生花的美妙

和爸爸妈妈共同完成一份特别的儿童节作品

简单四步，AI 涂鸦一键成画

基于 ModelArts，无需加载系统软件，购买计算资源，不懂代码也能使用 AI 将简单的涂鸦线稿一键成画。

ModelArts 是面向开发者的一站式 AI 开发平台，为机器学习与深度学习提供海量数据预处理及交互式智能标注、大规模分布式训练、自动化模型生成，及端 - 边 - 云模型按需部署能力，帮助用户快速创建和部署模型，管理全周期 AI 工作流。

具体步骤如下

第一步：访问页面，点击「Run in ModelArts」按钮，进入到 ModelArts CodeLab 运行环境中。

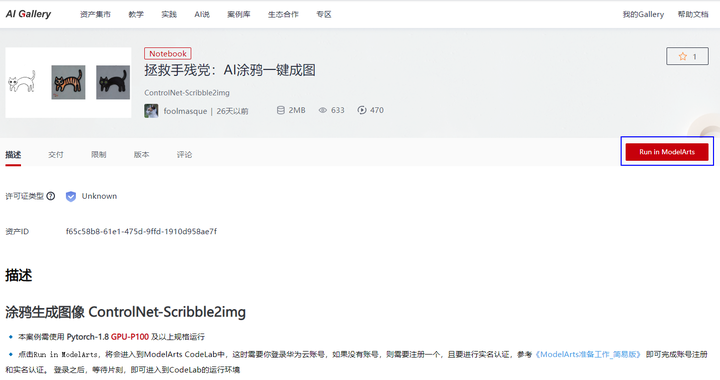
注：需先注册华为云账号并完成实名认证；若提示账号受限，退出账号重新登录即可。

第二步：切换运行环境，选择限时免费的 GPU-P100 规格，目前每个用户每天可以享受 3 小时的免费时长。然后点击代码块前面的三角形运行按钮，即可自动运行，完成模型的加载。

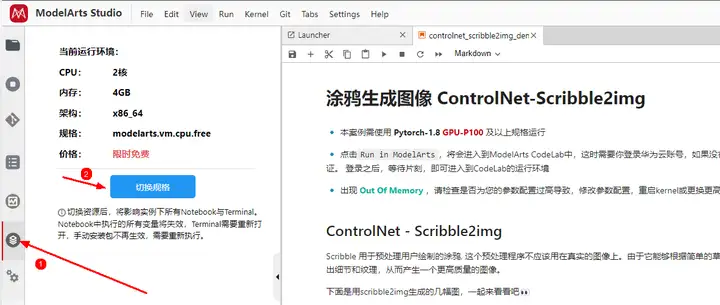
▲ 切换规格

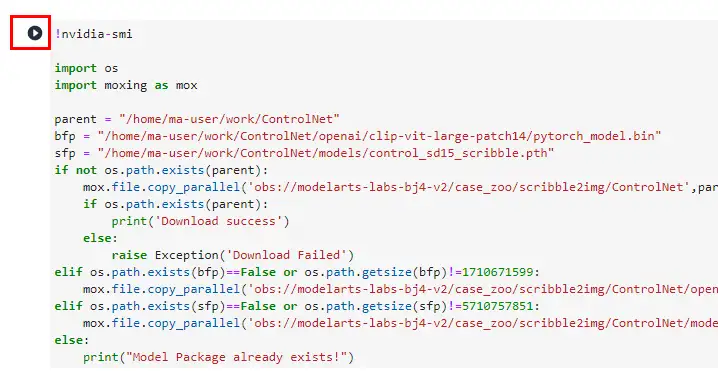
▲ 点击三角形按钮运行代码

第三步：依次运行完代码后，在右边文件夹 ControlNet/test_imgs/ 路径下，上传相册里的涂鸦图片。

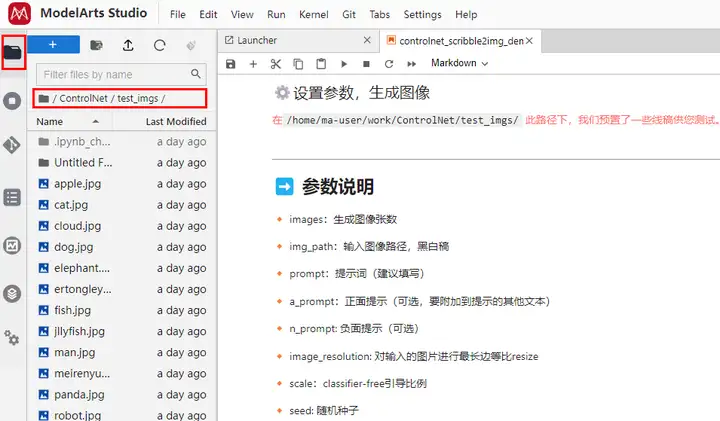
当然，如果你想涂鸦的同时生成图像，在 ModelArts 里通过 Gradio 可视化部署即可实现；也可以邀请朋友们一同创作，将生成的链接发给他们，就能直接通过手机或者电脑访问，在画布里自由创作。

第四步：设置你对图像的具体要求，例如画面的描述词、质量、剪裁等，生成图像。

简单四步

小朋友简单的涂鸦线稿

就变成各种自定义风格的艺术图像啦！

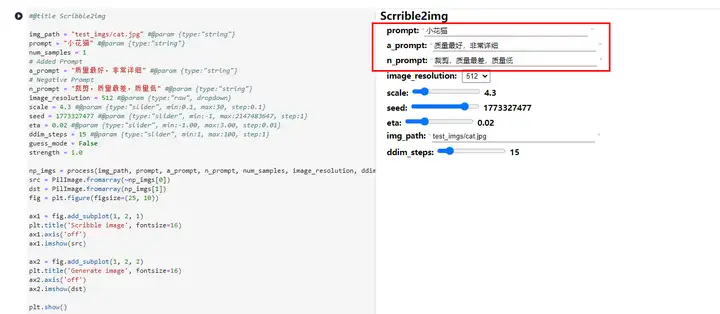
熊猫吃竹子

6 岁小朋友的 “熊猫吃竹子” 在华为云 ModelArts 的 AI 魔力下，秒变西直门三太子萌兰和成都顶流花花。

注：填写哪些提示词会影响最终生成的图像效果，通过不断调整 prompt、a_prompt、n_prompt 等参数，可以让熊猫更加完美哦！

“游乐场” 创想

还有这张 “游乐场” 创想，AI 妙笔生花，推理出了一座缤纷梦幻的儿童乐园。

寓教于乐，学学 AI 绘画背后的原理

说起当前 AIGC（AI Generated Content，人工智能自动生成内容）背后的热门技术，除了可以实现文本到图片的转化的 Stable Diffusion 模型，近期又有新的模型推出，就是上文我们用到的 ControlNet。

ControlNet 可以提高预训练的扩散模型的性能，特别是在预训练的扩散模型中加入它，能够使我们对图像的输出有更多的控制。ControlNet 提供了八个扩展，每个扩展都可以对扩散模型进行不同的控制。

本文提到的 AI 涂鸦一键成图主要是通过其中的 Scribble 来实现。它能够根据简单的草图，推理出更多细节，从而生成逼真或改进的图像。对于那些没有接受过美术训练或缺乏绘画天赋的人来说，这是非常棒的。

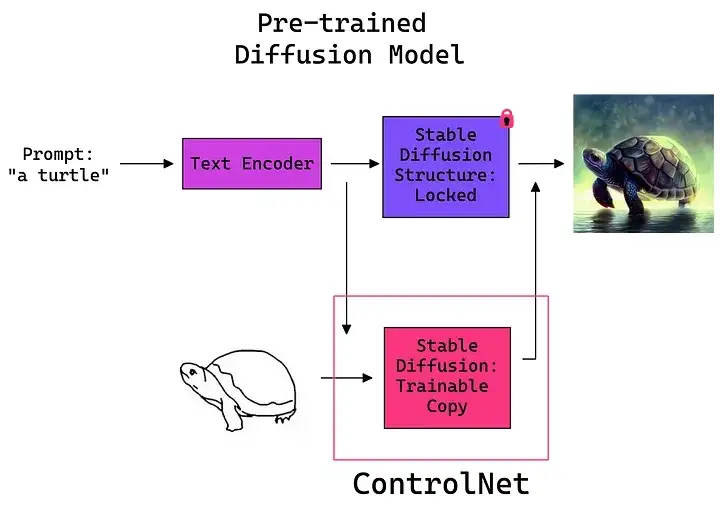
▲ ControlNet 模型的工作原理

▲ 使用 ControlNet-Scribble 输出的人像素描

上传你的作品，赢一波儿童节礼物！

看到这里，童心未泯的你是不是也想试试呢？在华为云 ModelArts 上传你的涂鸦线稿，一键生成精美画作，体验 Scribble2img 涂鸦生图的乐趣，将天马行空的想象变为真实的图像吧！

活动规则 【即日起至 6 月 8 日】

在 华为云AI Gallery评论区上传你的涂鸦原图和AI生成图片，我们将抽取质量较高的涂鸦成图运行作品，赠送漫威复仇者联盟乐高。

在 开发者论坛评论区参与活动，上传你的涂鸦生成图像，我们将在用户的有效作品当中抽取幸运儿赠送 Lebooo 电动牙刷。

注：两个活动可以同时参加，奖励不去重。

点击关注，第一时间了解华为云新鲜技术～