LIS和LCS算法分析

LIS（最长上升子序列）

常规的解法就是动态规划。

mx[ j ]表示长度为j的上升子序列最小的值a[i];

dp[ i ]表示前i个数的最长上升子序列长度多少。

 1 for(int i=1;i<n;i++)
 2  {
 3       int j;
 4       for( j=len;j>0;j--)
 5       {
 6            if(a[i]>mx[j])
 7            {
 8                  dp[i]=j+1;
 9                  mx[dp[i]]=min(mx[dp[i]],a[i]);//更新长度为j+1的最小值
10                  break;
11               }
12        }
13        if(j==0)//说明它是最小的
14        {
15              dp[i]=1;
16              mx[dp[i]]=min(mx[dp[i]],a[i]);//更新
17          }
18  }

这就是解决LIS的核心代码，时间复杂度网上的博客说复杂度是O(n²) 说实话，个人感觉没有那么高的复杂度，比如HDU-5532就可以用这个方法解决，但是如果按n*n的复杂度来说是肯定要tle的，结果时间是982ms。看了一下，甚至比其他的更快了一些。。。

LIS在时间上的优化那就只能用n*logn的算法了

这个算法其实已经不是DP了，有点像贪心。至于复杂度降低其实是因为这个算法里面用到了二分搜索。本来有N个数要处理是O(n)，每次计算要查找N次还是O(n)，一共就是O(n^2)；现在搜索换成了O(logn)的二分搜索，总的复杂度就变为O(nlogn)了。

ps：最近还没用这个算法，感觉dp就挺好用的，等用了在更新吧，hhhhhh

LCS(最长公共子序列)

既然放在一起写，那么肯定有共同的地方，原理还是dp。

感觉还是由一个题目来看看到底怎么解决吧。

LCS裸题：HDU-1159

Input

abcfbc abfcab
programming contest
abcd mnp

Output

4
2
0

Sample Input

abcfbc abfcab
programming contest
abcd mnp

Sample Output

4
2
0

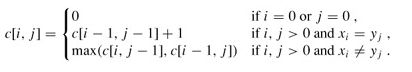
想一想是不是所有的情况都包括进去了

那么我们就可以在O(n*m)的复杂度解决这个问题了

 1 #include<iostream>
 2 #include<stdio.h>
 3 #include<algorithm>
 4 #include<string.h>
 5 using namespace std;
 6 char a[1050],b[1050];
 7 int dp[1050][1050];
 8 int main()
 9 {
10     while(~scanf("%s %s",&a,&b))
11     {
12         memset(dp,0,sizeof(dp));
13         int alen=strlen(a);
14         int blen=strlen(b);
15         for(int i=1;i<=alen;i++)
16         {
17             for(int j=1;j<=blen;j++)
18             {
19                 if(a[i-1]==b[j-1])
20                 {
21                     dp[i][j]=dp[i-1][j-1]+1;
22
23                 }
24                 else
25                 {
26                     dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
27                 }
28             }
29         }
30         cout<<dp[alen][blen]<<endl;
31     }
32     return 0;
33 }