算法：堆（Heap）

背景

Heap 可以用来实现优先级队列，也可以用来做堆排序，本文简单的做个介绍。

Heap

规则

• 是一个完全二叉树，隐含的意思是：他是平衡的、使用数组进行存储也是连续的。
• 给定的任意节点，该节点小于等于其父亲节点，大于他们的孩子节点。

基础知识

对于一个完全二叉树，如果将其存储到数组中，给定父节点的索引为：x，则：

• left child's index is：2*x + 1。
• right child's index is：2*x + 2。
• root's index is：0.

说明：上面的公式很容易自己推到出来，有兴趣的朋友可以推到一下，这样就不用记住这个特性了。

图示

存储到数组的顺序为：先存储第一层，然后是第二层，直到第 N 层。

操作

添加和删除后还必须保证 Heap 满足规则。

添加

添加前

添加 6

先将 6 添加到完全树的下一个节点，然后沿着祖先路径，将其插入到合适的节点（不一定是根节点）。

代码

             public void Insert(T item)
             {
                 if (this.IsFull())
                 {
                     throw new InvalidOperationException("容量已满，不能插入！");
                 }

                 _items[_length++] = item;
                 this.MoveUp(_length - );
             }

结果

删除最大值

接着上面的例子执行删除

先将删除根节点（6），再将完全树最后的节点（2）直接移动到根节点。

接着将 2 向下插入到合适的节点，比如：5 > 4 && 5 > 2，因此结果是：

代码

             public T Remove()
             {
                 if (this.IsEmpty())
                 {
                     throw new InvalidOperationException("容量已空，不能删除！");
                 }

                 var result = _items[];
                 _items[] = _items[--_length];

                 this.MoveDown();

                 return result;
             }

完整代码

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;

 namespace DataStuctureStudy.Heaps
 {
     class HeapTest
     {
         public static void Test()
         {
             var heap = new Heap<int>();
             heap.Insert();
             heap.Insert();
             heap.Insert();
             heap.Insert();
             heap.Insert();
             heap.Insert();
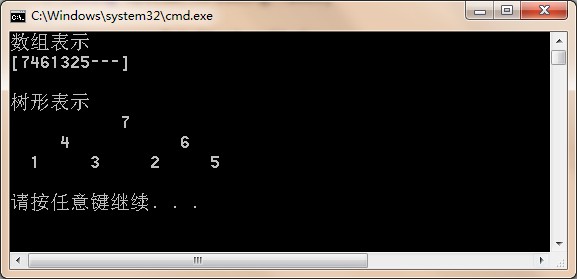
             heap.Display();
             heap.Remove();
             heap.Display();
         }

         class Heap<T>
             where T : IComparable<T>
         {
             private T[] _items;
             private int _length;

             public Heap(int size)
             {
                 _items = new T[size];
             }

             public void Display()
             {
                 Console.WriteLine("数组表示");
                 Console.Write("[");
                 for (var i = ; i < _items.Length; i++)
                 {
                     if (i < _length)
                     {
                         Console.Write(_items[i]);
                     }
                     else
                     {
                         Console.Write('-');
                     }
                 }
                 Console.WriteLine("]");
                 Console.WriteLine();

                 Console.WriteLine("树形表示");
                 var row = ;
                 var column = ;
                 var level = (int)Math.Ceiling(Math.Log(_length + , ));
                 var width = (int)Math.Pow(, level);
                 for (var i = ; i < _length; i++)
                 {
                     this.Display(_items[i], width, row, column);

                     if ((i + ) == Math.Pow(, row + ) - )
                     {
                         row++;
                         column = ;
                         Console.WriteLine();
                     }
                     else
                     {
                         column++;
                         if (i == _length - )
                         {
                             Console.WriteLine();
                         }
                     }
                 }

                 Console.WriteLine();
             }

             private void Display(T item, int width, int row, int column)
             {
                 var step = (int)((width * ) / Math.Pow(, row));
                 var itemLength = item.ToString().Length;
                 Console.Write(item.ToString().PadLeft((step + itemLength) / ).PadRight(step));
             }

             public void Insert(T item)
             {
                 if (this.IsFull())
                 {
                     throw new InvalidOperationException("容量已满，不能插入！");
                 }

                 _items[_length++] = item;
                 this.MoveUp(_length - );
             }

             private void MoveUp(int index)
             {
                 var bottom = _items[index];
                 var current = index;

                 while (current > )
                 {
                     var parent = (current - ) / ;
                     if (_items[parent].CompareTo(bottom) > )
                     {
                         break;
                     }

                     _items[current] = _items[parent];
                     current = parent;
                 }

                 _items[current] = bottom;
             }

             public T Remove()
             {
                 if (this.IsEmpty())
                 {
                     throw new InvalidOperationException("容量已空，不能删除！");
                 }

                 var result = _items[];
                 _items[] = _items[--_length];

                 this.MoveDown();

                 return result;
             }

             private void MoveDown(int index)
             {
                 var top = _items[index];
                 var current = index;

                 while (current < _length)
                 {
                     var large = ;
                     var left =  * current + ;
                     var right = left + ;

                     if (left < _length && right < _length)
                     {
                         if (_items[left].CompareTo(_items[right]) >= )
                         {
                             large = left;
                         }
                         else
                         {
                             large = right;
                         }
                     }
                     else if (left < _length)
                     {
                         large = left;
                     }
                     else
                     {
                         break;
                     }

                     if (_items[large].CompareTo(top) <= )
                     {
                         break;
                     }

                     _items[current] = _items[large];
                     current = large;
                 }

                 _items[current] = top;
             }

             public bool IsFull()
             {
                 return _length == _items.Length;
             }

             public bool IsEmpty()
             {
                 return _length == ;
             }
         }
     }
 }

备注

下篇简单的介绍一下堆排序。