再谈 最速下降法/梯度法/Steepest Descent

转载请注明出处：http://www.codelast.com/

最速下降法（又称梯度法，或Steepest Descent），是无约束最优化领域中最简单的算法，单独就这种算法来看，属于早就“过时”了的一种算法。但是，它的理念是其他某些算法的组成部分，或者说是在其他某些算法中，也有最速下降法的“影子”。因此，我们还是有必要学习一下的。
我很久以前已经写过一篇关于最速下降法的文章了，但是这里我还打算再写一篇，提供更多一些信息，让大家可以从更简单生动的方面去理解它。

『1』名字释义
最速下降法只使用目标函数的一阶导数信息——从“梯度法”这个名字也可见一斑。并且，它的本意是取目标函数值“最快下降”的方向作为搜索方向。于是我们就想知道这个问题的答案：沿什么方向，目标函数 f(x) 的值下降最快呢？

『2』函数值下降最快的方向
先说结论：沿负梯度方向 d=−gk，函数值下降最快。
下面就来推导一下。
将目标函数f(x)在点xk处泰勒展开（这是我们惯用的“伎俩”了）——
f(x)=f(xk)+αgTkdk+o(α)
高阶无穷小o(α)可忽略，由于我们定义了步长α>0，因此，当gTkdk<0时，f(x)<f(xk)，即函数值是下降的。此时dk就是一个下降方向。
但是dk具体等于什么的时候，可使目标函数值下降最快呢？
文章来源：http://www.codelast.com/
由Cauchy-Schwartz不等式（柯西-许瓦兹不等式）可得：
∣∣dTkgk∣∣≤∥dk∥∥gk∥
当且仅当dk=gk时，等号成立，dTkgk最大（>0）。
所以dk=−gk时，dTkgk最小（<0），f(x)下降量最大。
所以−gk是最快速下降方向。

『3』缺点
它真的“最快速”吗？答案是否定的。
事实是，它只在局部范围内具有“最速”性质。
对整体求解过程而言，它的下降非常缓慢。

『4』感受一下它是如何“慢”的
先来看一幅图（直接从维基百科上弄过来的，感谢Wiki）：

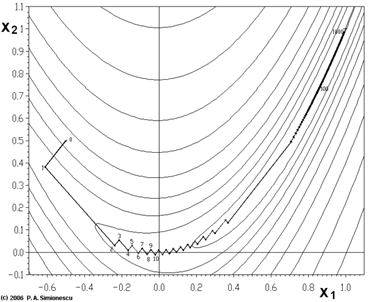
文章来源：http://www.codelast.com/
这幅图表示的是对一个目标函数的寻优过程，图中锯齿状的路线就是寻优路线在二维平面上的投影。
这个函数的表达式是：
f(x1,x2)=(1−x1)2+100⋅(x2−x12)2
它叫做Rosenbrock function（罗森布罗克方程），是个非凸函数，在最优化领域，它通常被用来作为一个最优化算法的performance test函数。
我们来看一看它在三维空间中的图形：

文章来源：http://www.codelast.com/
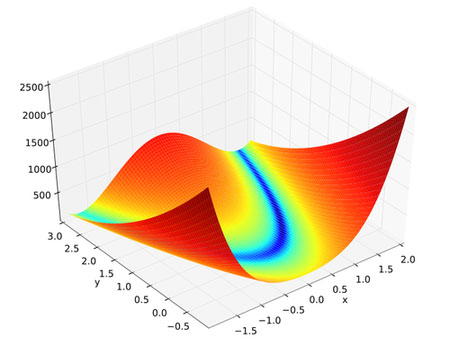
它的全局最优点位于一个长长的、狭窄的、抛物线形状的、扁平的“山谷”中。

找到“山谷”并不难，难的是收敛到全局最优解（全局最优解在 (1,1) 处）。

正所谓：世界上最遥远的距离，不是你离我千山万水，而是你就在我眼前，我却要跨越千万步，才能找到你。

文章来源：http://www.codelast.com/
我们再来看另一个目标函数f(x,y)=sin(12x2−14y2+3)cos(2x+1−ey)的寻优过程：

和前面的Rosenbrock function一样，它的寻优过程也是“锯齿状”的。
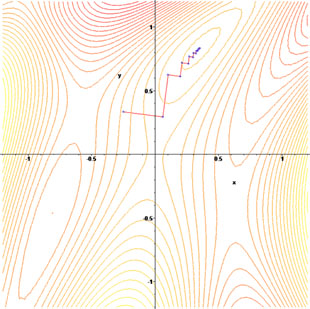
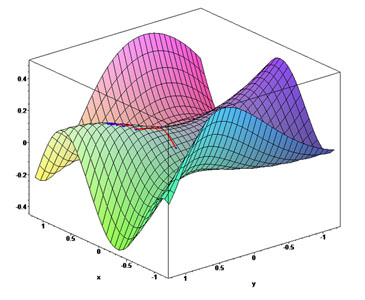
它在三维空间中的图形是这样的：

总而言之就是：当目标函数的等值线接近于圆(球)时，下降较快；等值线类似于扁长的椭球时，一开始快，后来很慢。

文章来源：http://www.codelast.com/
『5』为什么“慢”的分析
上面花花绿绿的图确实很好看，我们看到了那些寻优过程有多么“惨烈”——太艰辛了不是么？
但不能光看热闹，还要分析一下——为什么会这样呢？
由精确line search满足的一阶必要条件，得：
∇f(xk+αkdk)Tdk=0，即gTk+1dk=0
故由最速下降法的dk=−gk得：
gTk+1dk=gTk+1(−gk)=−gTk+1gk=−dTk+1dk=0⇒dTk+1dk=0
即：相邻两次的搜索方向是相互直交的（投影到二维平面上，就是锯齿形状了）。
文章来源：http://www.codelast.com/
如果你非要问，为什么dTk+1dk=0就表明这两个向量是相互直交的？那么我就耐心地再解释一下：
由两向量夹角的公式：

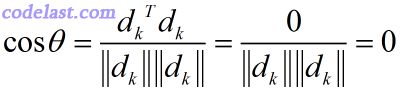
=> θ=π2
两向量夹角为90度，因此它们直交。

『6』优点
这个被我们说得一无是处的最速下降法真的就那么糟糕吗？其实它还是有优点的：程序简单，计算量小；并且对初始点没有特别的要求；此外，许多算法的初始/再开始方向都是最速下降方向（即负梯度方向）。
文章来源：http://www.codelast.com/
『7』收敛性及收敛速度
最速下降法具有整体收敛性——对初始点没有特殊要求。
采用精确线搜索的最速下降法的收敛速度：线性。