【C/C++】n皇后问题/全排列/递归/回溯/算法笔记4.3

按常规，先说一下我自己的理解。

递归中的return常用来作为递归终止的条件，但是对于返回数值的情况，要搞明白它是怎么返回的。递归的方式就是自己调用自己，而在有返回值的函数中，上一层的函数还没执行完就调用下一层，因此，当达到递归终止条件时，首先return的是最底层调用的函数，return之后，继续执行上一层调用该函数之后的代码，此时我们看到的是上一层的情况，当上一层剩余的代码执行完之后，表示上一层的函数也结束，此时再返回上上一层，执行递归代码之后的代码，如此往复循环，直到返回到最上层，结束整个递归过程。需要注意的是，上一层执行递归之后的代码的时候，会调用下一层返回的值，也可以理解为在执行上一层代码的时候会调用下一层的实现过程，直到下一层执行完返回一个数值，然后再加上上一层的数值，就构成了上一层return的东西，如此往复。

摘自CSDN

注意这个return，return是返回上一层，而不是跳出回到主函数。

然后如果不是return，在当前层没有可以执行的东西的时候，也跳回到上一层。

下面我们来看算法笔记中的全排列和n皇后问题。

n皇后问题

n皇后问题是指在一个n*n的国际象棋棋盘上放置n个皇后，使得这n个皇后两两均不在同一行、同一列、同一对角线上，求合法的方案数。

（我第一反应这不是图论里的匹配嘛……也可以点着色（x）

因为如果枚举n*n种情况的位置，选择n个，计算量太大，所以我们只考虑全排列情况，然后剔掉不满足不在同一对角线上的情况。

法1：枚举

这里枚举出n长数列的全排列，然后剔掉不满足不在同一对角线上的情况。

全排列：给出1~n的数字，给出所有的排列方式（不重复）。（Ann）

递归思想：

1. 递归边界：
2. 递归本体：假设已经填好了P[1]~P[index-1]，正准备填P[index]. 枚举x从1到n，如果hashtable[x] == false，就把它填到index中。然后递归下一位。
   
   递归完成后，把这一位的hashtable[x]释放。

判断：到达边界（输出）的时候，判断是不是在同一对角线上。

#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 11;
int n;
int P[maxn];
bool hashTable[maxn] = {false};

int cnt = 0;

void show_hashTable()
{
   for (int i = 1; i <= n; i++)
   {
      printf("%d ", hashTable[i]);
   }
   printf("\n");
}

void generateP(int index)
{
   if(index == n+1) //递归边界，边界先判断，只算结果
   {
      for(int i = 1; i <= n; i++)
      {
         printf("%d", P[i]);
      }
      printf("\n");
      return;
      // bool flag = true;  //flag为true表示当前排列合法
      // for(int i = 1; i <= n; i++)  //遍历任意两个皇后
      // {
      //    for(int j = i + 1; j <=n; j++)
      //    {
      //       if(abs(i - j) == abs(P[i] - P[j]))  //如果在一条对角线上
      //       {
      //          flag = false;  //不合法
      //       }
      //    }
      // }
      // if(flag) cnt++;
      // return;
   }
   for(int x = 1; x <= n; x++)
   {
      printf("x %d\n", x);
      if(hashTable[x] == false)
      {
         P[index] = x;
         //show_hashTable();
         hashTable[x] = true;
         generateP(index + 1);
         hashTable[x] = false;
         //show_hashTable();
      }
   }

}

int main()
{
   scanf("%d", &n);
   generateP(1);
   printf("%d\n", cnt);

   system("pause");
}

这段代码是怎么运行的？

我实在是好奇，然后就一步一步尝试了一下。

为了方便理解起见，这里选n=3.

结果是123 132 213 231 312 321

自带字典序。

 for(int x = 1; x <= n; x++)
   {
      printf("x %d\n", x);
      if(hashTable[x] == false)
      {
         P[index] = x;
         //show_hashTable();
         hashTable[x] = true;
         generateP(index + 1);
         hashTable[x] = false;
         //show_hashTable();
      }
   }

我做了一个这段代码的运行原理：

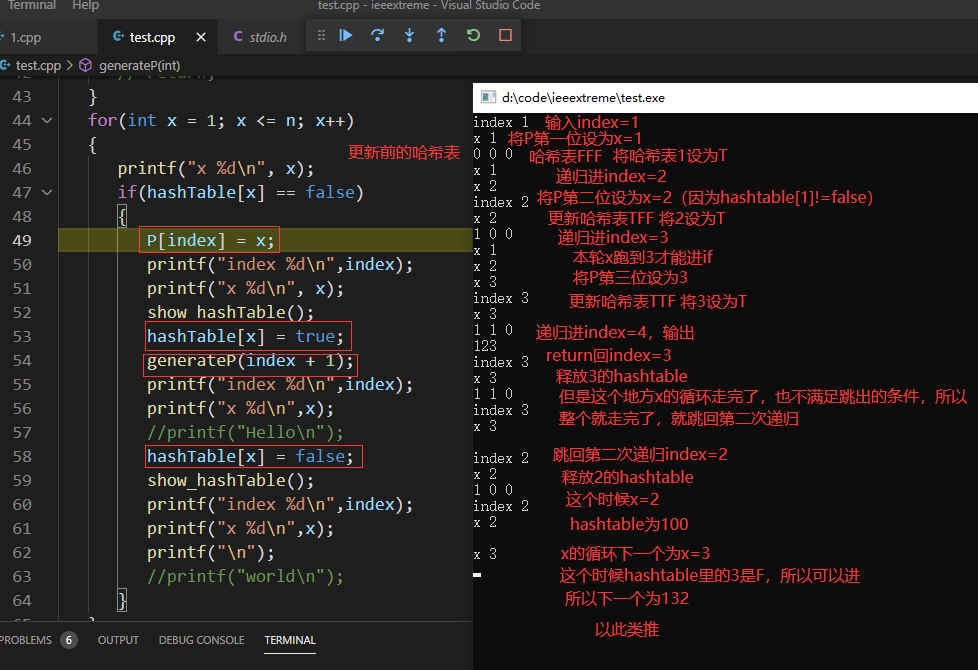
法2：回溯

定义：在到达递归前的某层，由于一些事实导致已经不需要往任何一个子问题递归，就可以直接返回上一层。

从代码编写上来看，其实就是把判断放到了递归的最开头。

#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 11;
int n;
int P[maxn];
bool hashTable[maxn] = {false};

int cnt = 0;

void show_hashTable()
{
   for (int i = 1; i <= n; i++)
   {
      printf("%d ", hashTable[i]);
   }
   printf("\n");
}

void generateP(int index)
{
   if(index == n+1) //递归边界，边界先判断，只算结果
   {
      for(int i = 1; i <= n; i++)
      {
         printf("%d", P[i]);
      }
      printf("\n");
      cnt++;
      return;
      // bool flag = true;  //flag为true表示当前排列合法
      // for(int i = 1; i <= n; i++)  //遍历任意两个皇后
      // {
      //    for(int j = i + 1; j <=n; j++)
      //    {
      //       if(abs(i - j) == abs(P[i] - P[j]))  //如果在一条对角线上
      //       {
      //          flag = false;  //不合法
      //       }
      //    }
      // }
      // if(flag) cnt++;
      // return;
   }
   for(int x = 1; x <= n; x++)
   {
      //printf("x %d\n", x);
      if(hashTable[x] == false)
      {
         bool flag = true; //表示可行
         for (int pre = 1; pre < index; pre++) //考察index之前的是否会与index冲突
         {
            if (abs(index - pre) == abs(x - P[pre]))
            {
               flag = false;
               break; //已经设置了flag，很保险；break只是为了节约不要后面无意义的for循环
            }
         }
         if (flag)
         {
            P[index] = x;
            hashTable[x] = true;
            generateP(index + 1);
            hashTable[x] = false;
         }
      }

   }

}

int main()
{
   scanf("%d", &n);
   generateP(1);
   printf("%d\n", cnt);

   system("pause");
}