Kolmogorov–Smirnov test(KS)

sklearn实战-乳腺癌细胞数据挖掘( 博主亲自录制)

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

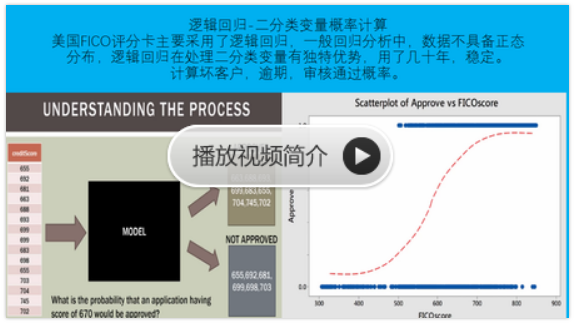
（三）KS检验

将KS检验应用于信用评级模型主要是为了验证模型对违约对象的区分能力，通常是在模型预测全体样本的信用评分后，将全体样本按违约与非违约分为两部分，然后用KS统计量来检验这两组样本信用评分的分布是否有显著差异。

两条曲线算的是累计概率

计算各阶段的差值

最后算差值的最大值

KS检验也常用来选择有预测能力的单变量。就是通过某个单变量把样本分成两组，看这两组的样本有关KS指标的大小来决定此变量的预测能力。

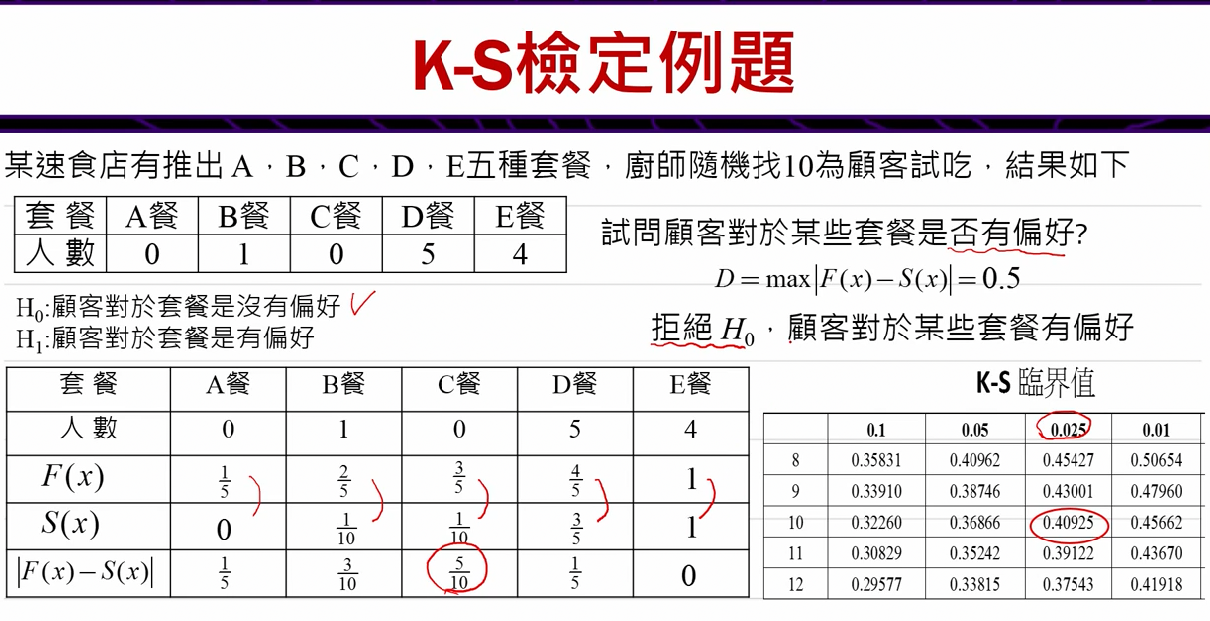
模型应该要能区别出违约户和正常户之间的差异，违约户的评级分配应当不同于正常户的评级分配。运用KS检验来验证模型能否区别出违约户与正常户，当两组样本的累积相对次数分配非常接近，且差异为随机时，则两组样本的评级分配应为一致；反之当两组样本的评级分配并不一致时，样本累积相对次数分配的差异会很显，如下图所示：

KS检验模型区分能力

对总体十等分，并按照违约率降序排序，计算每一等分中违约与正常百分比的累计分布，绘制出两者差异

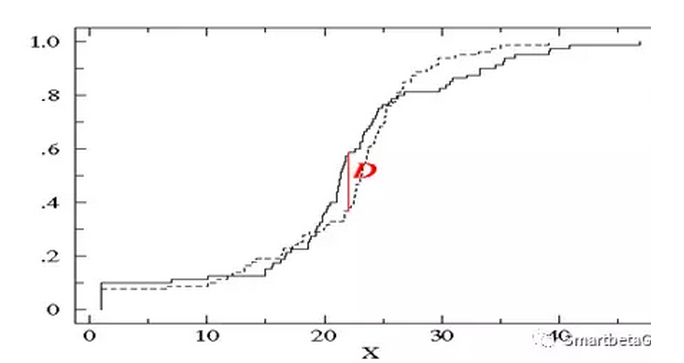
KS的检验步骤为：

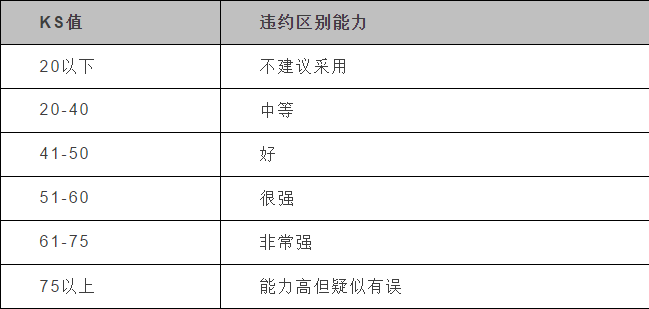
KS值越大，表示模型能够将正、负客户区分开的程度越大。 
通常来讲，KS>0.2即表示模型有较好的预测准确性。

1、计算正常户和违约户在各评分阶段下的累积比率

2、 计算各阶段累积比率之差

3、 找出最大的累积比率之差，即为KS

另外，下表为KS值对应违约区别能力：

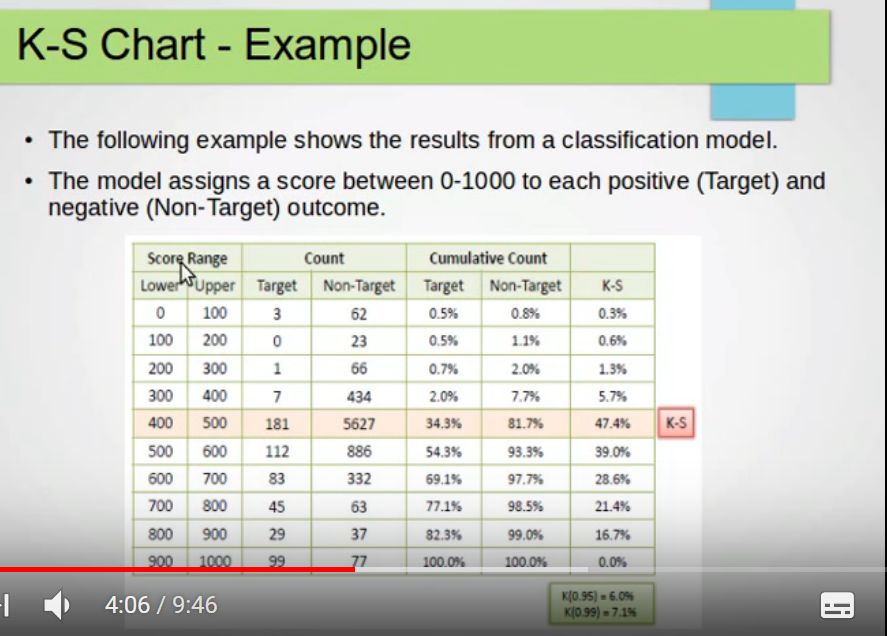
假设模型分数有0-1000分

分数分为10个阶段

一阶段：0-100分

二阶段：100-200分

三阶段：200-300分

.........

十阶段：900-1000分

计算每个阶段坏客户累积占比和好客户累积占比，例如第五阶段，坏客户累积占比34%，好客户累积占比81%，差值47.4%，最大

47%超过阈值20%，模型区分能力非常强

ks即使显著，分数段预测准确率也不一定高

使用K-S检验一个数列是否服从正态分布、两个数列是否服从相同的分布

假设检验的基本思想：

若对总体的某个假设是真实的，那么不利于或者不能支持这一假设的事件A在一次试验中是几乎不可能发生的。如果事件A真的发生了，则有理由怀疑这一假设的真实性，从而拒绝该假设。

实质分析：

假设检验实质上是对原假设是否正确进行检验，因此检验过程中要使原假设得到维护，使之不轻易被拒绝；否定原假设必须有充分的理由。同时，当原假设被接受时，也只能认为否定该假设的根据不充分，而不是认为它绝对正确。

1、检验指定的数列是否服从正态分布

借助假设检验的思想，利用K-S检验可以对数列的性质进行检验，看代码：

from scipy.stats import kstest
import numpy as np

x = np.random.normal(0,1,1000)
test_stat = kstest(x, 'norm')

 

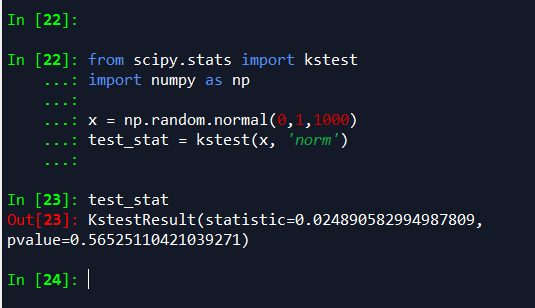
首先生成1000个服从N(0,1)标准正态分布的随机数，在使用k-s检验该数据是否服从正态分布，提出假设：x从正态分布。

最终返回的结果，p-value=0.76584491300591395，比指定的显著水平（假设为5%）大，则我们不能拒绝假设：x服从正态分布。

这并不是说x服从正态分布一定是正确的，而是说没有充分的证据证明x不服从正态分布。因此我们的假设被接受，认为x服从正态分布。

如果p-value小于我们指定的显著性水平，则我们可以肯定的拒绝提出的假设，认为x肯定不服从正态分布，这个拒绝是绝对正确的。

2、检验指定的两个数列是否服从相同分布

　　

from scipy.stats import ks_2samp
beta=np.random.beta(7,5,1000)
norm=np.random.normal(0,1,1000)
ks_2samp(beta,norm)

　　

 

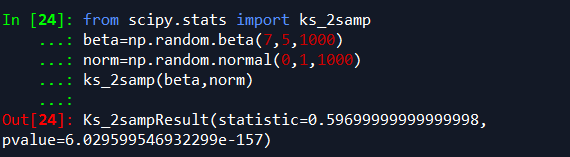
我们先分别使用beta分布和normal分布产生两个样本大小为1000的数列，使用ks_2samp检验两个数列是否来自同一个样本，提出假设：beta和norm服从相同的分布。

最终返回的结果，p-value=4.7405805465370525e-159，比指定的显著水平（假设为5%）小，则我们完全可以拒绝假设：beta和norm不服从同一分布。

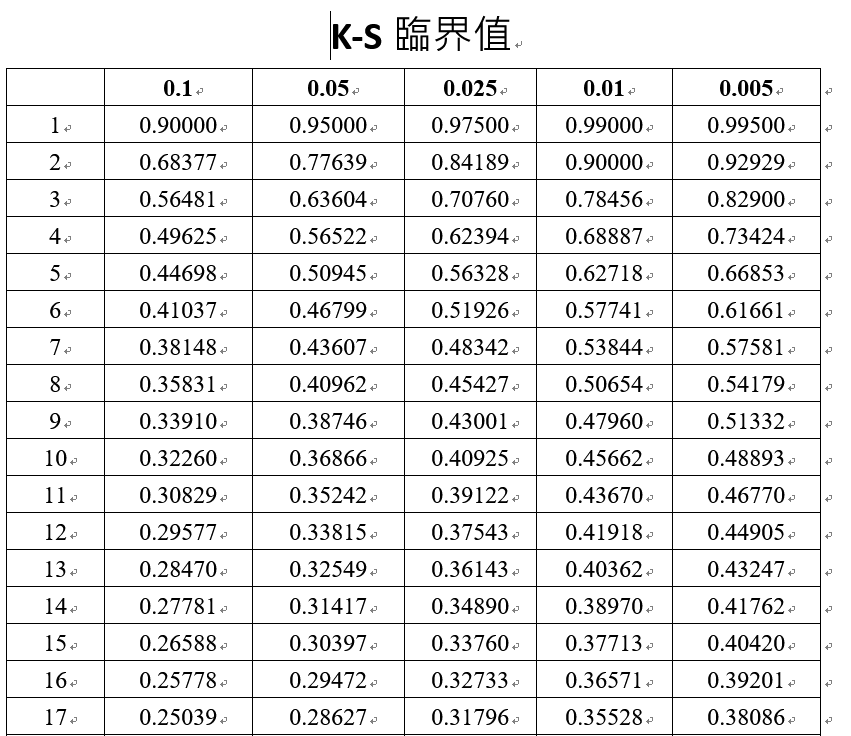
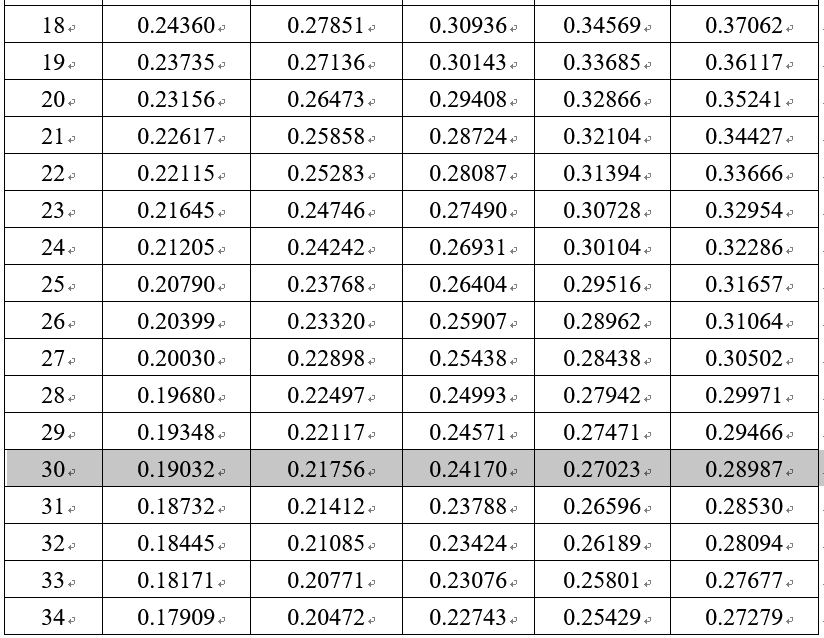
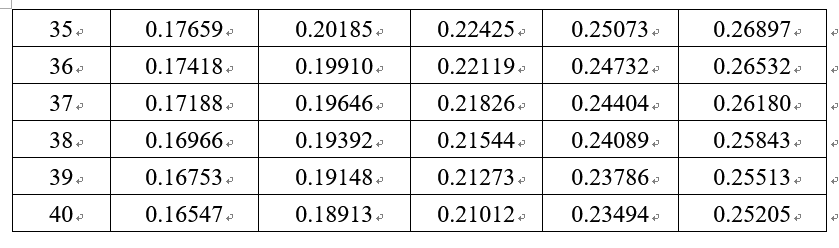
KS临界值表

www.cust.edu.tw/mathmet/KS-critical.docx

python风控评分卡建模和风控常识

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share