何为仿射变换(Affine Transformation)

http://www.cnblogs.com/ghj1976/p/5199086.html

变换模型是指根据待匹配图像与背景图像之间几何畸变的情况，所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种:刚性变换、仿射变换、透视变换和非线形变换等，如下图：

参考： http://wenku.baidu.com/view/826a796027d3240c8447ef20.html

其中第三个的仿射变换就是我们这节要讨论的。

仿射变换(Affine Transformation) 
Affine Transformation是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直性”（译注：straightness，即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（译注：parallelness，其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变。）。

c和d的区别可以看下图：

仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。

仿射变换可以用下面公式表示：

参考：http://wenku.baidu.com/view/826a796027d3240c8447ef20.html

这个矩阵乘法的计算如下：

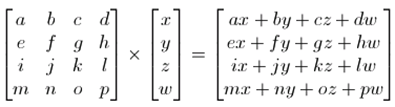
具体到二维的仿射变换的计算如下：

几种典型的仿射变换如下：

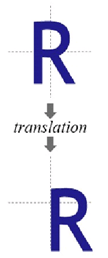
平移变换 Translation

将每一点移动到(x+tx, y+ty)，变换矩阵为： 

平移变换是一种“刚体变换”，rigid-body transformation，就是不会产生形变的理想物体。

效果：

缩放变换（Scale）

将每一点的横坐标放大（缩小）至sx倍，纵坐标放大（缩小）至sy倍，变换矩阵为：

变换效果如下：

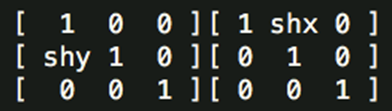
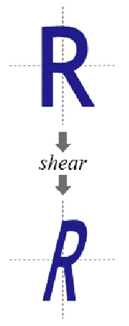
剪切变换（Shear）

变换矩阵为：

相当于一个横向剪切与一个纵向剪切的复合

效果：

旋转变换（Rotation）

目标图形围绕原点顺时针旋转theta弧度，变换矩阵为：

效果：

组合

旋转变换，目标图形以(x, y)为轴心顺时针旋转theta弧度，变换矩阵为：

相当于两次平移变换与一次原点旋转变换的复合：

先移动到中心节点，然后旋转，然后再移动回去。

参考： 
http://wenku.baidu.com/link?url=AtomIQH400RVIckGwh-V5vPBGmTEVN7ZBtzEjHFeEPxkqu2llowVdW1IFFPqJWaZGUQsQG1hK0OtdrFJ4JBsru3rO8bP9VKQ8Iae0Xm_wt7

这个转换矩阵也可以下面这样描述。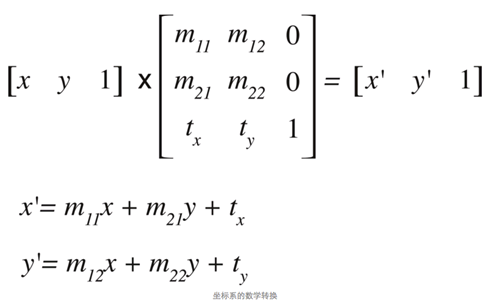 

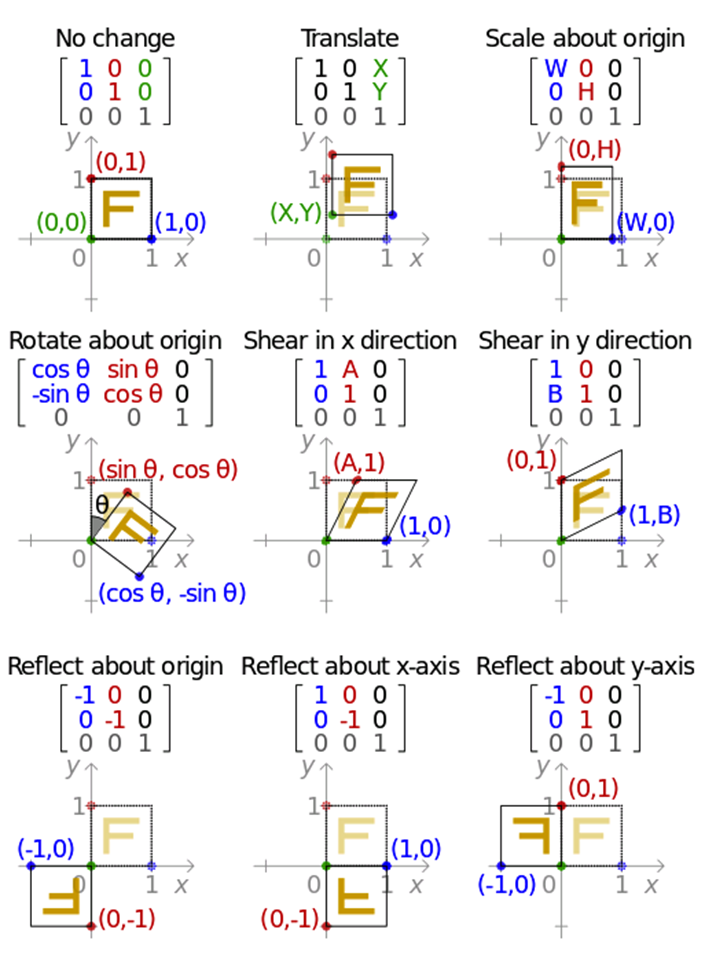
一些常用转换矩阵如下：