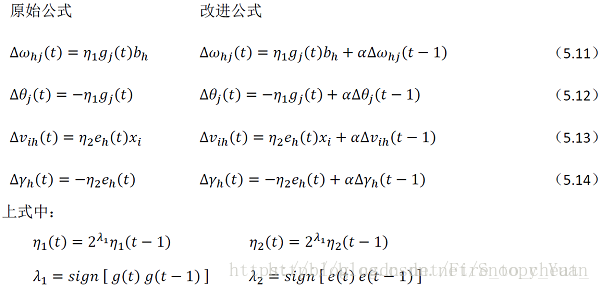BP神经网络算法改进
试设计一个算法,能通过动态调整学习率显著提升收敛速度,编程实现该算法,并选择两个UCI数据集与标准的BP算法进行实验比较。
1.方法设计
传统的BP算法改进主要有两类:
- 启发式算法:如附加动量法,自适应算法
- 数值优化法:如共轭梯度法、牛顿迭代法、Levenberg-Marquardt算法
(1)附加动量项
这是一种广泛用于加速梯度下降法收敛的优化方法。其核心思想是:在梯度下降搜索时,若当前梯度下降与前一个梯度下降的方向相同,则加速搜索,反之则降速搜索。
标准BP算法的参数更新项为:
Δω(t)=ηg(t)" role="presentation" style="position: relative;">Δω(t)=ηg(t)Δω(t)=ηg(t)
式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。" role="presentation" style="position: relative;">式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。
在添加动量项后,基于梯度下降的参数更新项为:
Δω(t)=η[(1−μ)g(t)+μg(t−1)]" role="presentation" style="position: relative;">Δω(t)=η[(1−μ)g(t)+μg(t−1)]Δω(t)=η[(1−μ)g(t)+μg(t−1)]
始终,μ" role="presentation" style="position: relative;">μμ为动量因子(取值 0~1)。上式也等价于:
Δω(t)=αΔω(t−1)+ηg(t)" role="presentation" style="position: relative;">Δω(t)=αΔω(t−1)+ηg(t)Δω(t)=αΔω(t−1)+ηg(t)
式中α" role="presentation" style="position: relative;">αα 称为遗忘因子,αΔω(t−1)" role="presentation" style="position: relative;">αΔω(t−1)αΔω(t−1)表示上一次梯度下降的方向和大小信息对当前梯度下降的调整影响。
(2) 自适应学习率
附加动量法面临选取率的选取困难,进而产生收敛速度和收敛性的矛盾。于是另考虑引入学习速率自适应设计,这里给出一个·自适应设计方案:
η(t)=ση(t−1)" role="presentation" style="position: relative;">η(t)=ση(t−1)η(t)=ση(t−1)
上式中,η(t)" role="presentation" style="position: relative;">η(t)η(t)为第t次迭代时的自适应学习速率因子,下面是一种计算实力:
σ(t)=2λ" role="presentation" style="position: relative;">σ(t)=2λσ(t)=2λ
其中λ" role="presentation" style="position: relative;">λλ为梯度方向:λ=sign(g(t)(t−1))" role="presentation" style="position: relative;">λ=sign(g(t)(t−1))λ=sign(g(t)(t−1))
这样,学习率的变化可以反映前面附加动量项中的“核心思想”。
(3)算法总结
将上述两种方法结合起来,形成动态自适应学习率的BP改进算法:

从上图及书中内容可知,输出层与隐层的梯度项不同,故而对应不同的学习率 η_1 和 η_2,算法的修改主要是第7行关于参数更新的内容:
将附加动量项与学习率自适应计算代入,得出公式(5.11-5.14)的调整如下图所示:
2.对比实验
BP神经网络算法改进的更多相关文章
- bp神经网络算法
对于BP神经网络算法,由于之前一直没有应用到项目中,今日偶然之时 进行了学习, 这个算法的基本思路是这样的:不断地迭代优化网络权值,使得输入与输出之间的映射关系与所期望的映射关系一致,利用梯度下降的方 ...
- 二、单层感知器和BP神经网络算法
一.单层感知器 1958年[仅仅60年前]美国心理学家FrankRosenblant剔除一种具有单层计算单元的神经网络,称为Perceptron,即感知器.感知器研究中首次提出了自组织.自学习的思想, ...
- BP神经网络算法预测销量高低
理论以前写过:https://www.cnblogs.com/fangxiaoqi/p/11306545.html,这里根据天气.是否周末.有无促销的情况,来预测销量情况. function [ ma ...
- 数据挖掘系列(9)——BP神经网络算法与实践
神经网络曾经很火,有过一段低迷期,现在因为深度学习的原因继续火起来了.神经网络有很多种:前向传输网络.反向传输网络.递归神经网络.卷积神经网络等.本文介绍基本的反向传输神经网络(Backpropaga ...
- BP神经网络算法学习
BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是眼下应用最广泛的神经网络模型之中的一个 ...
- BP神经网络算法推导及代码实现笔记zz
一. 前言: 作为AI入门小白,参考了一些文章,想记点笔记加深印象,发出来是给有需求的童鞋学习共勉,大神轻拍! [毒鸡汤]:算法这东西,读完之后的状态多半是 --> “我是谁,我在哪?” 没事的 ...
- R_Studio(神经网络)BP神经网络算法预测销量的高低
BP神经网络 百度百科:传送门 BP(back propagation)神经网络:一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最广泛的神经网络 #设置文件工作区间 setwd('D:\\ ...
- JAVA实现BP神经网络算法
工作中需要预测一个过程的时间,就想到了使用BP神经网络来进行预测. 简介 BP神经网络(Back Propagation Neural Network)是一种基于BP算法的人工神经网络,其使用BP算法 ...
- BP神经网络算法推导
目录 前置知识 梯度下降法 激活函数 多元复合函数求偏导的相关知识 正向计算 符号定义 输入层 隐含层 输出层 误差函数 反向传播 输出层与隐含层之间的权值调整 隐含层与输入层之间权值的调整 计算步骤 ...
随机推荐
- 各种Js插件汇总;JavaScript插件
1.jquery信息提示插件: https://blog.csdn.net/u013517229/article/details/78291841 http://www.jqueryfuns.com/ ...
- 运行mapreduce - java.lang.InterruptedException
错误日志: 2018-11-19 05:23:51,686 WARN [main] util.NativeCodeLoader (NativeCodeLoader.java:<clinit> ...
- Windows和linux双系统——改动默认启动顺序
电脑上装了Windows 7和Ubantu双系统,因为Linux系统用的次数比較少而且还是默认的启动项对此非常不能容忍,因此得改动Windows为默认的启动项. 因为电脑上的系统引导程序是GRUB,因 ...
- Android中的动画具体解释系列【2】——飞舞的蝴蝶
这一篇来使用逐帧动画和补间动画来实现一个小样例,首先我们来看看Android中的补间动画. Android中使用Animation代表抽象的动画类,该类包含以下几个子类: AlphaAnimation ...
- java 配置时遇到的问题及解决办法
1. 最近JDK更新很频繁,以至于我安装时版本太多,选择也会出现问题 首先,确定你选择的是32位版本还是64位版本(貌似64位系统下也可以安装32位的JDK), 这个相当重要,因为这个会影响到ecli ...
- 不同节点 IP 时间同步 分布式时间同步系统的参考时间获取技术分析
linux linux下时间同步的两种方法分享_LINUX_操作系统_脚本之家 http://www.jb51.net/LINUXjishu/73979.html 分布式时间同步系统的参考时间获取技术 ...
- tcp state
[root@hadoop1 log]# netstatActive Internet connections (w/o servers)Proto Recv-Q Send-Q Local Addres ...
- WebService注解汇总
Web Service 元数据注释(JSR 181) @WebService 1.serviceName: 对外发布的服务名,指定 Web Service 的服务名称:wsdl:service.缺省值 ...
- 设计模式-(14)装饰者模式 (swift版)
一,概念 装饰者模式(Decorator):动态地为一个对象添加一些额外的职责,若要扩展一个对象的功能,装饰者提供了比继承更有弹性的替代方案. 多组合,少继承 二,UML图 抽象构件类(Compone ...
- Python: PS 图像调整--亮度调整
本文用 Python 实现 PS 图像调整中的亮度调整,具体的算法原理和效果可以参考之前的博客: http://blog.csdn.net/matrix_space/article/details/2 ...