数值分析实验之曲线最小二乘拟合含有噪声扰动（python实现）

一、实验目的

掌握最小二乘法拟合离散数据，多项式函数形式拟合曲线以及可以其他可以通过变量变换转化为多项式的拟合曲线目前待实现功能：

1. 最小二乘法的基本实现。

2. 用不同数据量，不同参数，不同的多项式阶数，比较实验效果。

3. 语言python。

二、实验原理

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

三、实验内容

求y=f(x)=sin(x)+h(x)在区间[0,10]上按101等距节点确定的离散数据点组(x_i,y_i)的直线拟合以及曲线拟合，其中是服从h(x)标准正态分布的噪声扰动

四、程序实现

 • 一次拟合：

 import numpy as np
 import matplotlib.pyplot as plt
 import math
 #定义x、y散点坐标
 x = np.arange(0.0, 10.0,0.1)
 x = np.array(x)
 print('x is :\n',x)
 num = np.sin(x)+np.random.randn(100)
 y = np.array(num)
 print('y is :\n',y)
 f1 = np.polyfit(x, y, 1)#用1次多项式拟合，若要多次拟合，相应的改变这个常数即可
 print('f1 is :\n',f1)

 p1 = np.poly1d(f1)
 print('p1 is :\n',p1)

 #也可使用yvals=np.polyval(f1, x)
 yvals = p1(x)  #拟合y值
 print('yvals is :\n',yvals)
 #绘图
 plot1 = plt.plot(x, y, 's',label='original values',color="blue")
 plot2 = plt.plot(x, yvals, 'r',label='polyfit values',color="red")
 plt.xlabel('x')
 plt.ylabel('y')
 plt.legend(loc=4) #指定legend的位置右下角
 plt.title('polyfitting')
 plt.show()

运行结果：

所得图形：

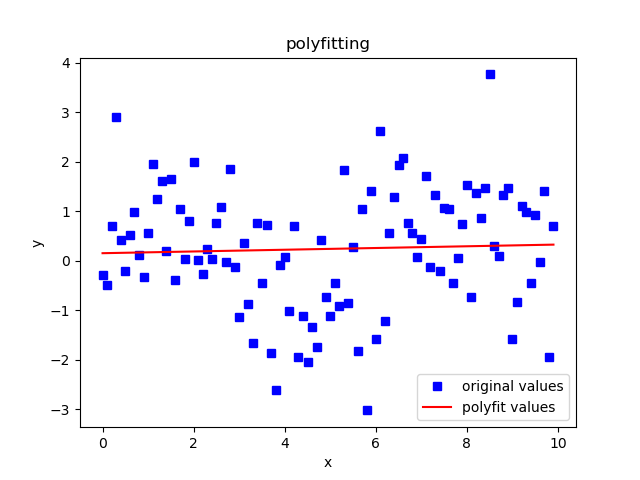
• 曲线拟合（用a*sin(x)+b拟合）：

 import numpy as np
 import matplotlib.pyplot as plt
 import math
 from scipy.optimize import curve_fit

 #自定义函数
 def func(x, a, b):
     return a*np.sin(x)+b

 #定义x、y散点坐标
 x = np.arange(0.0, 10.0,0.1)
 x = np.array(x)
 num = np.sin(x)+np.random.randn(100)
 y = np.array(num)

 #非线性最小二乘法拟合
 popt, pcov = curve_fit(func, x, y)
 #获取popt里面是拟合系数
 print(popt)
 a = popt[0]
 b = popt[1]
 #c = popt[2]
 #d = popt[3]
 #e = popt[4]
 yvals = func(x,a,b) #拟合y值
 print('popt:', popt)
 print('系数a:', a)
 print('系数b:', b)
 #print('系数c:', c)
 #print('系数d:', d)
 #print('系数e:', e)
 print('系数pcov:', pcov)#方差
 print('系数yvals:', yvals)#x代入拟合出的函数得到的函数值
 #绘图
 plot1 = plt.plot(x, y, 's',label='original values',color="purple")
 x_test = np.arange(0.0, 10.0, 0.01)
 y_test = func(x_test,a,b)
 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color="red")
 plt.xlabel('x')
 plt.ylabel('y')
 plt.legend(loc=4) #指定legend的位置右下角
 plt.title('curve_fit')
 plt.show()

运行结果

所得图形：

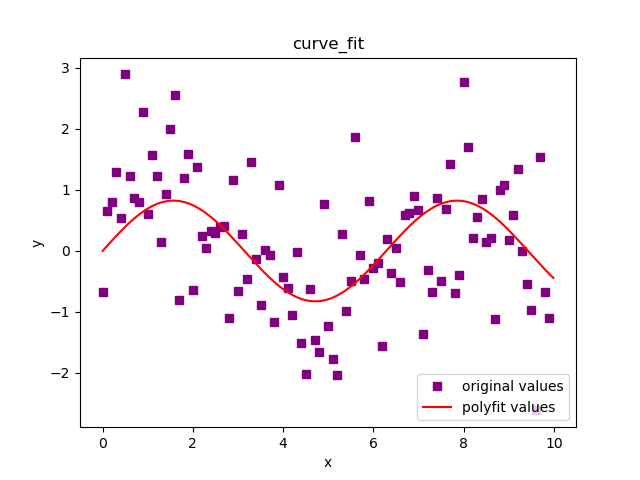
•曲线拟合（用a*np.sin(b*x+c)+d拟合）：

 import numpy as np
 import matplotlib.pyplot as plt
 import math
 from scipy.optimize import curve_fit

 #自定义函数
 def func(x, a, b, c, d):
     return a*np.sin(b*x+c)+d

 #定义x、y散点坐标
 x = np.arange(0.0, 10.0,0.1)
 x = np.array(x)
 num = np.sin(x)+np.random.randn(100)
 y = np.array(num)

 #非线性最小二乘法拟合
 popt, pcov = curve_fit(func, x, y)
 #获取popt里面是拟合系数
 print(popt)
 a = popt[0]
 b = popt[1]
 c = popt[2]
 d = popt[3]
 yvals = func(x,a,b,c,d) #拟合y值
 print('popt:', popt)
 print('系数a:', a)
 print('系数b:', b)
 print('系数c:', c)
 print('系数d:', d)
 print('系数pcov:', pcov)#方差
 print('系数yvals:', yvals)#x代入拟合出的函数得到的函数值
 #绘图
 plot1 = plt.plot(x, y, 's',label='original values',color='orange')
 x_test = np.arange(0.0, 10.0, 0.01)
 y_test = func(x_test,a,b,c,d)
 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color='brown')
 plt.xlabel('x')
 plt.ylabel('y')
 plt.legend(loc=4) #指定legend的位置右下角
 plt.title('curve_fit')
 plt.show()

运行结果：

所得图形：

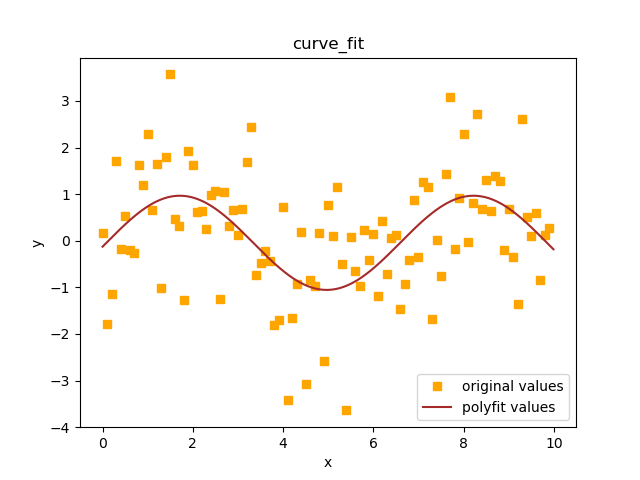
•自定义函数实现：

 import numpy as np
 import matplotlib.pyplot as plt
 import math
 from scipy.optimize import curve_fit

 #自定义函数
 def func(x, a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w):
     return  a0 + a1*np.cos(x*w) + b1*np.sin(x*w) + \
                a2*np.cos(2*x*w) + b2*np.sin(2*x*w) + a3*np.cos(3*x*w) + b3*np.sin(3*x*w) + \
                a4*np.cos(4*x*w) + b4*np.sin(4*x*w) + a5*np.cos(5*x*w) + b5*np.sin(5*x*w) + \
                a6*np.cos(6*x*w) + b6*np.sin(6*x*w) + a7*np.cos(7*x*w) + b7*np.sin(7*x*w) + \
                a8*np.cos(8*x*w) + b8*np.sin(8*x*w)

 #定义x、y散点坐标
 x = np.arange(0.0, 10.0,0.1)
 x = np.array(x)
 num = np.sin(x)+np.random.randn(100)
 y = np.array(num)

 #非线性最小二乘法拟合
 popt, pcov = curve_fit(func, x, y)
 #获取popt里面是拟合系数
 print(popt)
 a0 = popt[0]
 a1 = popt[1]
 a2 = popt[2]
 a3 = popt[3]
 a4 = popt[4]
 a5 = popt[5]
 a6 = popt[6]
 a7 = popt[7]
 a8 = popt[8]
 b1 = popt[9]
 b2 = popt[10]
 b3 = popt[11]
 b4 = popt[12]
 b5 = popt[13]
 b6 = popt[14]
 b7 = popt[15]
 b8 = popt[16]
 w = popt[17]
 yvals = func(x,a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w) #拟合y值
 print('popt:', popt)
 print('系数a0:', a0)
 print('系数a1:', a1)
 print('系数a2:', a2)
 print('系数a3:', a3)
 print('系数a4:', a4)
 print('系数a5:', a5)
 print('系数a6:', a6)
 print('系数a7:', a7)
 print('系数a8:', a8)
 print('系数b1:', b1)
 print('系数b2:', b2)
 print('系数b3:', b3)
 print('系数b4:', b4)
 print('系数b5:', b5)
 print('系数b6:', b6)
 print('系数b7:', b7)
 print('系数b8:', b8)
 print('系数w:', w)
 print('系数pcov:', pcov)#方差
 print('系数yvals:', yvals)#x代入拟合出的函数得到的函数值
 #绘图
 plot1 = plt.plot(x, y, 's',label='original values',color='yellow')
 x_test = np.arange(0.0, 10.0, 0.01)
 y_test = func(x_test,a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w)
 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color='blue')
 plt.xlabel('x')
 plt.ylabel('y')
 plt.legend(loc=4) #指定legend的位置右下角
 plt.title('curve_fit')
 plt.show()

实现结果：

所得图形：

心得体会

通过本次实验，我对MATLAB的操作更加熟悉，也对本学期正在学习的Python有了更深层次的认识，对着两种编程软件更加熟悉。最重要的是：对最小二乘法理解深入，以及可以应用推广，对数值分析理论的学习有很重要的作用，总而言之收获颇多。