接受H0的坏处|试验误差|置信度由来|

生物统计与实验设计

置信度（0.05 0.01）是通过实验次数估计值的分布得到的，它是整个分布的期望，这个值的确立需要具体情况具体分析。

肯定很难，因为否定一次很容易。虽然如果没有否定（eg：得到p=0.03即服从0.01下的H0成立），但是仍存在0.01下H0不成立，从而在该置信度下接受H1假设。所以，总是存在小概率事件发生的情况，所以不能因为接受H0假设而认为H0假设成立，接受H0假设不能说明任何事情，所以，研究者期待的结果是拒绝H0而接受H1假设，因为到此就停止了，此时的状态称为具有显著性。

假设检验：（hypothesis test）又称为显著性检验，它的基本思想是小概率反证法，过程对参数假设一个值，判断该假设是否成立。

描述统计是表达数据信息；而推断检验是为了一叶知秋，这两者关系如下：

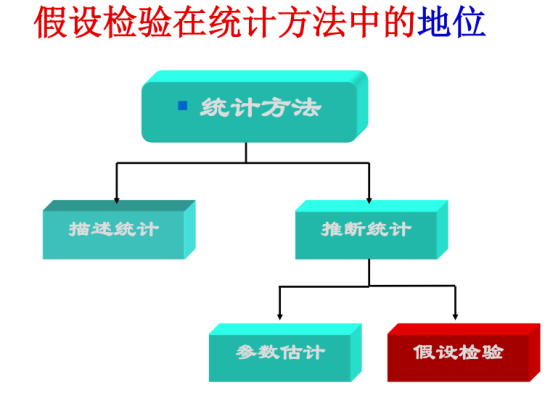
假设检验包括参数（要求学习的内容）和非参（不要求学习的内容）

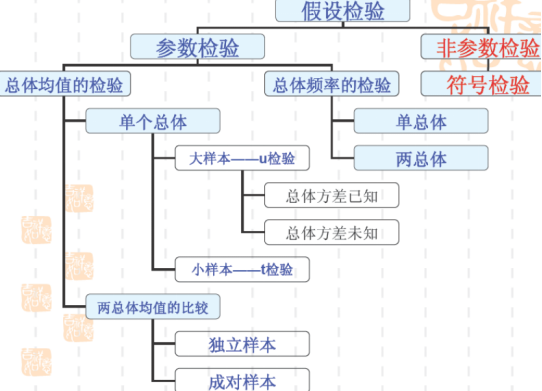
相同条件是除控制变量外都一致。

样本平均数包含总体平均数与试验误差二部分，所以样本平均数与总体平均数的差值便是实验误差，此实验误差有量纲，可以使用除标准差的形式将量纲除去，变成一个纯数值。

在比较两个数值是否相等时，可将两数值样本均值的差（表面误差）作为新变量，将两数据的均值差作为新参数（真实差异），而两数据之间的随机误差的差值作为新误差（实验误差），这样可以规避由于物理因素造成的误差，只留下随机误差（抽样引发的误差）。

假设检验流程：

1.提出假设（此时需要关注非此即彼的问题）：假设一般是认为真实差异为0（即没差异），所以表面误差（x bar）实际上就是实验误差。由常数确定显著性水平，该常数来源于分布，最后归在单个值上。

2.计算概率即是计算表面误差是随机误差的概率，标准化之后的变量服从标准正态分布，该变量是实验误差。小样本采用t检验的原因是，小样本由于样本数目小，所以每一个样本的权重比较大，而恰好t检验对n值敏感（一个n一条曲线分布），所以使用t检验。

3.推断时需要注意服从H0会有不好结果。