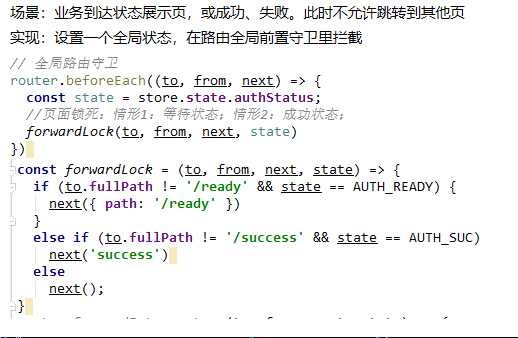
vue页面固定锁死
vue页面固定锁死的更多相关文章
- iframe嵌套vue页面打开新窗口
iframe嵌套vue页面时目录结构为下图: 此时出口文件指向index.html, 所以只需要用a标签动态拼接href, 并设置属性 target="_blank" ,即可在if ...
- python 全栈开发,Day92(编程式的导航,vue页面布局,marked包的使用)
昨日内容回顾 1. 组件间的传值 1. bus --> 空Vue对象 通过向bus对象抛出自定义事件的方式在组件间传递信息 2. 注意事项: 1. bus.$on()应该在组件mounted(挂 ...
- 帮助快速生成页面固定显示元素的jQuery插件 - sticky-kit
来源:GBin1.com 如果需要在用户滚动页面的时候,保持特定元素始终可见的话,今天这里我们介绍的Sticky-Kit是一个不错的选择. 它是一个开源的jQuery插件,可以帮助大家快速针对页面元素 ...
- Vue页面骨架屏(一)
在开发webapp的时候总是会受到首屏加载时间过长的影响,主流的解决方法是在载入完成之前显示loading图效果,而一些大公司会配置一套服务端渲染的架构来解决这个问题.考虑到ssr所要解决的一系列问题 ...
- Vue页面间传值,以及客户端数据存储
初学Vue,遇到了页面传值的问题,大概网上学习了解了一下,在此跟大家分享一下学习心得,欢迎批评指正. 一.参数传值 如果是简单的页面传值,比如传一个id到详情页等等,推荐使用参数传值. 这里页面是通过 ...
- URL不变的情况下,最实用的vue刷新当前页面,provide / inject 组合 方式实现vue页面刷新
原文:https://blog.csdn.net/Dream_xun/article/details/83024487 其他参考:https://blog.csdn.net/liyunkun888/a ...
- vue页面顺序规范
// html模板<template> <div>因联vue页面规范</div></template><script> // 模块 ...
- Vue页面缓存和不缓存的方法
第一步 在app中设置需要缓存的div //缓存的页面 <keep-alive> <router-view v-if="$route.meta.keepAlive" ...
- Vue 页面 前进刷新 后退不刷新(keepAlive)
前言 遇到这一个个问题 需要是这样的 Vue里面的不刷新问题 页面分为: A 主页 B列表页 C 详情页 A beforeRouteLeave 时设置 to.meta.keepAlive = ...
随机推荐
- 团队选题报告(bull beer)
一.团队成员及分工 团队名称:bull beer 团队成员: 黄文东:选题报告word撰写 沈培:原型设计,博客撰写,ppt制作 邓泽中:住院 刘帅:查找相关资料 二.选题报告内容 项目名称:学费管理 ...
- 常见形式 Web API 的简单分类总结
一.请求--响应API. 请求--响应类的API的典型做法是,通过基于HTTP的Web服务器暴露一个/套接口.API定义一些端点,客户端发送数据的请求到这些端点,Web服务器处理这些请求,然后返回响应 ...
- python获取set-cookies
python获取set-cookies #!/usr/bin/python3.4 # -*- coding: utf-8 -*- import requests url = "https:/ ...
- 【机器学习】--鲁棒性调优之L1正则,L2正则
一.前述 鲁棒性调优就是让模型有更好的泛化能力和推广力. 二.具体原理 1.背景 第一个更好,因为当把测试集带入到这个模型里去.如果测试集本来是100,带入的时候变成101,则第二个模型结果偏差很大, ...
- .NET Core实战项目之CMS 第一章 入门篇-开篇及总体规划
作者:依乐祝 原文地址:https://www.cnblogs.com/yilezhu/p/9977862.html 写在前面 千呼万唤始出来,首先,请允许我长吸一口气!真没想到一份来自28岁老程序员 ...
- 《前端之路》之三 数组的属性 && 操作方法(上)
目录 03:数组的属性 && 操作方法(上) 03:数组的属性 && 操作方法(上) 一.Array property 数组的属性 1.constructor 返回对创 ...
- celery异步消息处理框架
Celery 1.什么是Clelery Celery是一个简单.灵活且可靠的,处理大量消息的分布式系统 专注于实时处理的异步任务队列 同时也支持任务调度 Celery架构 Celery的架构由三部分组 ...
- javascript 函数后面有多个小括号f( )( )( )...
有时我们看见js函数后面跟着多个小括号是什么意思?f( )( )( )... f()执行f函数,返回子函数 f()()执行子函数,返回孙函数 f()()()执行孙函数,返回重孙函数 ... ... 但 ...
- css3动画--位移加阴影
animation: name duration timing-function delay iteration-count direction; 值 描述 animation-name 规定需要绑定 ...
- Java初学习-常见单词
implements 实行/实现 用于实现接口(interface) extends 延伸/扩展 用于类的继承 container 容 ...
