Script Component 引用package variable

scipy包提供了几种通用的插补工具，分别用于1维，2维或高维的数据集，分别是：

类 interp1d 用于对一维数据进行插补
类 griddata 提供了对1D，2D和高维数据进行插补的工具。
spline插补，用于对一维和二维数据进行平滑的cubic-spline 插补
使用基于径向的函数（RBF）进行插值

这些方法都集成在scipy.interpolate模块中。

一，interp1d类

一维插补类(interp1d)，是一种基于一维固定数据点创建函数的便捷方法，该函数内推一个一元的函数f，使得 y=f(x)：

scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)

kind 参数用于指定内推的类型，(‘linear’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’, ‘previous’, ‘next’和 ‘nearest’。对于'linear'，是默认值，表示线性插补，前面已描述；对于 ‘zero’, ‘slinear’, ‘quadratic’ 和 ‘cubic’ 引用的是spline内推，使用 zeroth, first, second 和 third 顺序。对于 ‘previous’ 、 ‘next’ 和 ‘nearest’ 简单返回数据点的前一个、后一个或最近的一个数据。

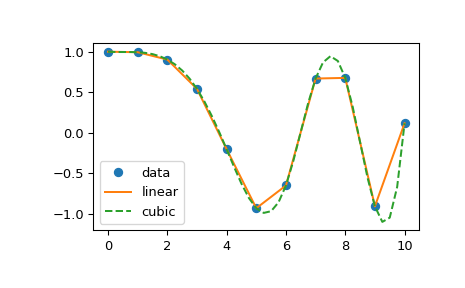
举个例子，使用interp1d内推两个函数，并绘制两个函数插补的数据点：

>>> import scipy

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)

>>> y = np.cos(-x**2/9.0)

>>> f = interp1d(x, y)

>>> f2 = interp1d(x, y, kind='cubic')

>>> xnew = np.linspace(0, 10, num=41, endpoint=True)

>>> import matplotlib.pyplot as plt

>>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')>>> plt.legend(['data', 'linear', 'cubic'], loc='best')

>>> plt.show()

二，多变量插补（griddata）

对于多维的数据，维度之间是相互关联的，例如，age、education和income是相互关联的，可以认为income = f(age,education)。对于二维数据，使用griddata 内推一个二元函数，z=f(x,y)。

scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)

参数注释：

points：自变量，对于二元函数而言，points是指由(x,y)构成的数据点
values：因变量，values是指某一个数据点的值，对于二元函数而言，数据点(x,y)的值是z=f(x,y)
xi：坐标系，或者说是数据点在坐标系中的位置，也可以把points的值作为坐标系的x和y轴，把values作为坐标系的z轴
method：有效值是‘linear’, ‘nearest’, ‘cubic’

三，spline类

一维spline的处理过程分为两个基本步骤：计算曲线的spline表示，对目标点进行评估。scipy有两种方式来计算曲线的spline表示和平滑系数：直接方式和参数化方式。

1，直接方式

直接方式使用splrep()函数从2维平面中查找曲线的spline表示，x和y是曲线在二维坐标系中的坐标。

splrep()函数的作用是对于给定数据点集（x [i]，y [i]），确定在间隔xb <= x <= xe上平滑度为k的近似值。

scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, task=0, s=None, t=None, full_output=0, per=0, quiet=1)

参数注释：

x和y定义一个曲线，y=f(x)
w 权重，用于在spline拟合时计算加权最小二乘法的值，w的默认值为1/(len(x))。如果y值中的误差是向量d给出的标准偏差，则w应为1 / d。
xb，xe：用于拟合的间隔，如果没有指定，那么默认值分别是x[0] 和 x[-1]。
k 用于指定spline order，默认值是3，字符串表示为cubic，k的取值区间是[1,5]
s 用于制定平滑条件，满足以下条件来确定平滑度：sum（（w *（y-g））** 2，axis = 0）<= s，其中g（x）是（x，y）的平滑插值。用户可以使用s来控制贴合度和平滑度之间的权衡，较大的s表示更平滑，而较小的s值表示较不平滑。s的推荐值取决于权重w。如果权重代表y的标准偏差的倒数，则应在（m-sqrt（2 * m），m + sqrt（2 * m））范围内找到一个好的s值，其中m是 x，y和w中的数据点。默认值：如果提供了权重，则s = m-sqrt（2 * m）。如果未提供权重，则s = 0.0（内插）。

该函数输出的结果是一个三元组tck，这个三元组就是曲线的spline表示，用于表示曲线的节点向量、系数和spline序号，默认的spline orde是cubic，这可以通过k参数来修改。一旦确定了曲线的spline表示，就可以使用splev()函数对x进行评估：

scipy.interpolate.splev(x, tck, der=0, ext=0)

举个例子，使用splrep()函数来获取曲线的spline表示，也就是tck，再通过tck和splev()函数来评估曲线：

>>> import matplotlib.pyplot as plt

>>> from scipy.interpolate import splev, splrep

>>> x = np.linspace(0, 10, 10)

>>> y = np.sin(x)

>>> spl = splrep(x, y)

>>> x2 = np.linspace(0, 10, 200)

>>> y2 = splev(x2, spl)

>>> plt.plot(x, y, 'o', x2, y2)

>>> plt.show()

2，参数化方式

对于在N维空间中的区间，使用函数splprep()来定义曲线的参数：

scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None, full_output=0, nest=None, per=0)

参数注释：

x：代表N维空间中曲线的N个数组的列表，每个数组的长度都是曲线的点的数量，每一个数组都提供N维数据点的一个分量。
u：是参数值的数组，该参数默认为0到1之间的等距单调序列，计算公式是：

M = len(x[0]), where v[0] = 0
v[i] = v[i-1] + distance(x[i], x[i-1])
u[i] = v[i] / v[M-1]

ub,ue：参数间隔的端点，默认值是 u [0]和u [-1]。
k：spline拟合的度，推荐使用默认值k=3，表示cubic，k的取值区间是[1,5]
s：平滑度，是0到1之间的小数，0表示不平滑，值越大，平滑度越高。
per：如果非0，那么把数据点视为周期性曲线，周期为x [m-1]-x [0]，并返回平滑的周期样条近似。

默认输出包含两个对象：第一个对象是一个三元祖(t,c,k)，分别表示曲线的节点向量、系数和spline序号；第二个对象是一个参数变量u。

对于函数splprep() 返回的spline表示，使用splev()函数来评估

>>> from scipy.interpolate import splprep, splev

>>> tck, u = splprep([x, y], s=0)

>>> new_points = splev(u, tck)

>>> import matplotlib.pyplot as plt

>>> fig, ax = plt.subplots()

>>> ax.plot(x, y, 'ro')

>>> ax.plot(new_points[0], new_points[1], 'r-')

>>> plt.show()

参考文档：

SciPy documentation

SciPy tutorial.