[NOI2010][bzoj2005] 能量采集 [欧拉函数+分块前缀和优化]

题面：

传送门

思路：

稍微转化一下，可以发现，每个植物到原点连线上植物的数量，等于gcd(x,y)-1，其中xy是植物的横纵坐标

那么我们实际上就是要求2*sigma(gcd(x,y))-n*m了

又有某不知名神奇定理：一个数的所有因子的phi之和等于这个数本身，其中phi是欧拉函数

因此题目转化为求如下：

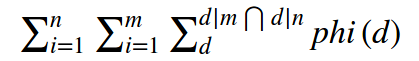
我们把式子变个型，就成了如下式子：

然后一个前缀和优化，O(n+sqrt(n))解决

Code：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #define ll long long
 using namespace std;
 inline ll read(){
     ll re=,flag=;char ch=getchar();
     while(ch>''||ch<''){
         if(ch=='-') flag=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='') re=(re<<)+(re<<)+ch-'',ch=getchar();
     return re*flag;
 }
 ll phi[],pri[],cnt,pre[];
 void init(){
     phi[]=pre[]=;ll i,j,k;
     for(i=;i<=;i++){
         if(!phi[i]) phi[i]=i-,pri[++cnt]=i;
         for(j=;(j<=cnt)&&(i*pri[j]<=);j++){
             if(i%pri[j]) phi[i*pri[j]]=phi[i]*(pri[j]-);
             else{phi[i*pri[j]]=phi[i]*pri[j];break;}
         }
         pre[i]=pre[i-]+phi[i];
 //        if(i<=10) cout<<"phi "<<i<<" "<<phi[i]<<"\n";
     }
 }
 ll n,m;ll ans;
 int main(){
     init();ll i,j;
     n=read();m=read();
     if(n>m) swap(n,m);
     for(i=;i<=n;i=j+){
         j=min(n/(n/i),m/(m/i));
         ans+=(ll)(n/i)*(m/i)*(pre[j]-pre[i-]);
     }
     printf("%lld\n",ans*-n*m);
 }

∑ni=1∑mi=1∑d|m⋂d|ndphi(d)

∑ni=1∑mi=1∑d|m⋂d|ndphi(d)