机器学习之PCA主成分分析

前言

           以下内容是个人学习之后的感悟，转载请注明出处~

简介

　　在用统计分析方法研究多变量的课题时，变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的

信息较多。在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反

映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量(关系紧密的变量)删去多余，建立

尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

　　降维算法有很多，比如PCA、ICA、SOM、MDS、ISOMAP、LLE等，在此不一一列举。PCA是一种无监督降维算法，

它是最常用的降维算法之一，可以很好地解决因变量太多而复杂性、计算量增大的弊端。

PCA主成分分析原理

1、协方差原理

　　样本X和样本Y的协方差(Covariance)：

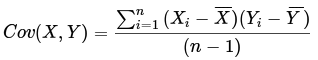
　　协方差为正时说明X和Y是正相关关系，协方差为负时X和Y是负相关关系，协方差为0时X和Y相互独立。Cov(X,X)就是

X的方差(Variance).当样本是n维数据时，它们的协方差实际上是协方差矩阵（对称方阵），方阵的边长是C_n²。比如对于3

维数据(x,y,z)，计算它的协方差就是：

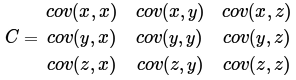
2、SVD分解原理

　　若AX=λX，则称λ是A的特征值，X是对应的特征向量。实际上可以这样理解：矩阵A作用在它的特征向量X上，仅仅使得

X的长度发生了变化，缩放比例就是相应的特征值λ。当A是n阶可逆矩阵时，A与P^-1Ap相似，相似矩阵具有相同的特征值。

　　特别地，当A是对称矩阵时，A的奇异值等于A的特征值，存在正交矩阵Q（Q^-1=Q^T），使得：

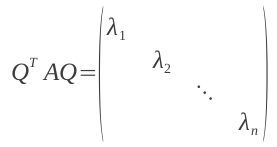
　　对A进行奇异值分解就能求出所有特征值和Q矩阵。A∗Q=Q∗D,D是由特征值组成的对角矩阵由特征值和特征向量的定

义知，Q的列向量就是A的特征向量。

3、PCA原理及实现

　　PCA主要通过把数据从高维映射到低维来降低特征维度。如下图所示，但映射的时候要保留尽量多的主要信息。

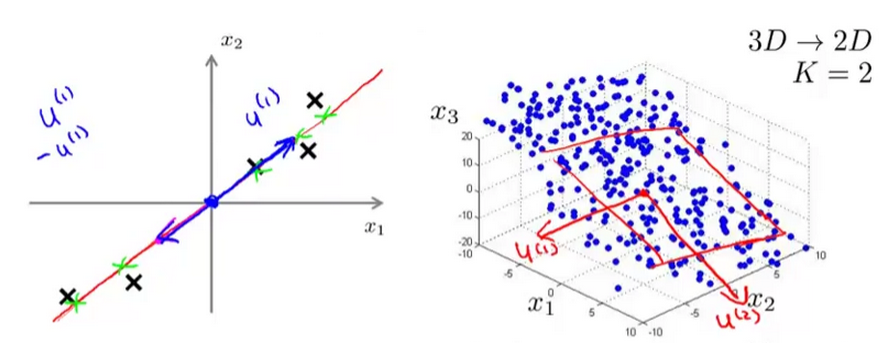
　　PCA的算法步骤如下：

• 输入数据集x={x⁽¹⁾，x⁽²⁾，x⁽³⁾，.....，x^(m)}、需要降到K维；
• 对所有样本进行均值归一化，如右图所示；　
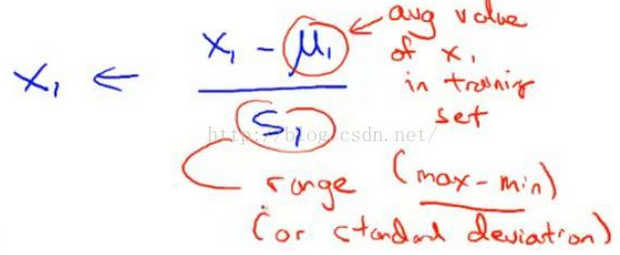
• 计算协方差矩阵
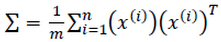
• 对协方差矩阵进行奇异值分解；
• 选取最大的前K个特征值对应的特征向量u⁽¹⁾，u⁽²⁾，u⁽³⁾，.....，u^(k)
• 输出降维的投影特征矩阵Ureduce={u⁽¹⁾，u⁽²⁾，u⁽³⁾，.....，u^(k)}
• 输出降维后的数据集z=Ureduce^Tx

4、选择降维后的维度K（主成分的个数）

　　如何选择主成分个数K呢？先来定义两个概念：

　　选择不同的K值，然后用下面的式子不断计算，选取能够满足下列式子条件的最小K值即可。

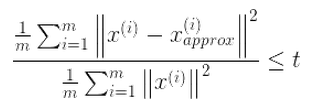
　　其中t值可以由自己定，比如t值取0.01，则代表了该PCA算法保留了99%的主要信息。当你觉得误差需要更小，

你可以把t值设的更小。上式还可以用SVD分解时产生的S矩阵来表示，如下面的式子：

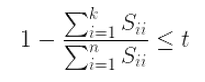
　　注意1：虽然PCA有降维的效果，也许对避免过拟合有作用，但是最好不要用PCA去作用于过拟合。

　　注意2：在训练集中找出PCA的主成分，（可以看做为映射 mapping），然后应用到测试集和交叉验

　　证集中。而不是对所有数据集使用PCA然后再划分训练集，测试集和交叉验证集。

以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~