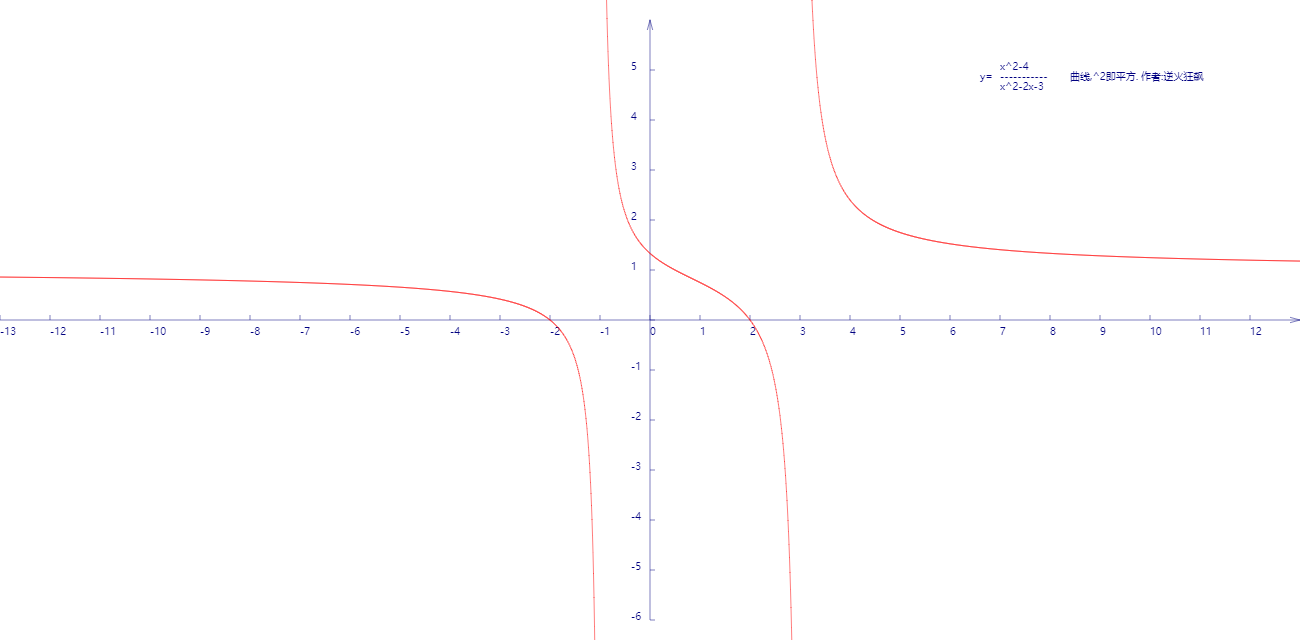
在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线

<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
     <title>函数x^2-4/x^2-2x-3曲线勾画</title>
    </head>

     <body onload="draw()">
        <canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
            出现文字表示你的浏览器不支持HTML5
        </canvas>
     </body>
</html>
<script type="text/javascript">
<!--
    function draw(){
        var canvas=document.getElementById("myCanvus");
        var canvasWidth=1300;
        var canvasHeight=640;

        var context=canvas.getContext("2d");

        context.fillStyle = "white";
        context.fillRect(0, 0, canvasWidth, canvasHeight);

        context.strokeStyle = "black";
        context.fillStyle = "black";

        // 进行坐标变换：把原点放在左下角，东方为X轴正向，北方为Y轴正向
        var offsetY=320;// Y向偏移值，正值向上偏，用来画坐标轴
        var offsetX=650;// X向偏移值，正值向右偏，用来画坐标轴

        context.save();
        context.translate(0+offsetX,canvasHeight-offsetY);

        drawAxisXText(context);// 文字和线分开画比较好处理
        drawAxisYText(context);
        drawTitleText(context);

        context.rotate(getRad(180));
        context.scale(-1,1);        

        drawAxisX(context);
        drawAxisY(context);
        drawCurve(context);       

        context.restore();
    }

    function drawTitleText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var x=350;
        var y=-250;

        // 写文字
        ctx.fillText("x^2-4",x,y);
        ctx.fillText("-----------",x,y+10);
        ctx.fillText("x^2-2x-3",x,y+20);
        ctx.fillText("y=",x-20,y+10);
        ctx.fillText("曲线,^2即平方. 作者:逆火狂飙",x+70,y+10);
    }

    function drawCurve(ctx){
        var SU=50;// Scale Unit

        var cds=[{}];
        var cds1=[{}];
        var cds2=[{}];

        var x,y;
        for(x=-13;x<=13;x+=0.01){

            if(x<-1){
                y=(x*x-4)/(x*x-2*x-3);// 函数式在此
                var arr={"x":x,"y":y};
                cds.push(arr);
            }

            if(x>-1 && x<3){
                y=(x*x-4)/(x*x-2*x-3);// 函数式在此
                var arr={"x":x,"y":y};
                cds1.push(arr);
            }

            if(x>3 ){
                y=(x*x-4)/(x*x-2*x-3);// 函数式在此
                var arr={"x":x,"y":y};
                cds2.push(arr);
            }
        }

        // 将数组里面的点一段段连线
        //var ymax=-6,ymin=6,xmax,xmin;

        ctx.strokeStyle = "red";
        ctx.beginPath();

        for(var i=0; i<cds.length; i++){
            ctx.lineTo(cds[i].x*SU,cds[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        ctx.beginPath();
        for(var i=0; i<cds1.length; i++){
            ctx.lineTo(cds1[i].x*SU,cds1[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        ctx.beginPath();
        for(var i=0; i<cds2.length; i++){
            ctx.lineTo(cds2[i].x*SU,cds2[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        // 极大值
        /*ctx.beginPath();
        ctx.moveTo(xmax*SU,ymax*SU-5);
        ctx.lineTo(xmax*SU,ymax*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymax="+cutShort(ymax.toString(),8),xmax*SU,-ymax*SU);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();

        // 极小值
        ctx.beginPath();
        ctx.moveTo(xmin*SU,ymin*SU-5);
        ctx.lineTo(xmin*SU,ymin*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymin="+ymin,xmin*SU,-ymin*SU);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();*/
    }

    function drawAxisX(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(start, 0);
        ctx.lineTo(end, 0);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
        ctx.lineTo(end, 0);
        ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        y=5;
        for(x=start;x<end;x+=50){
            ctx.beginPath();
            ctx.moveTo(x, 0);
            ctx.lineTo(x, y);

            ctx.stroke();
            ctx.closePath();
        }

        ctx.restore();
    }

    function drawAxisXText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 写文字
        var x,y=5;
        for(x=start;x<end;x+=50){
            ctx.fillText(x/50,x,y+10);
        }
    }

    function drawAxisY(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-300;
        var end=300;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(0, start);
        ctx.lineTo(0, end);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.lineTo(0, end);
        ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        x=5;
        for(y=start;y<end;y+=50){
            ctx.beginPath();
            ctx.moveTo(x, y);
            ctx.lineTo(0, y);

            ctx.stroke();
            ctx.closePath();
        }
    }

    function drawAxisYText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-250;
        var end=350;

        // 写文字
        var x=-19,y=5;
        for(y=start;y<end;y+=50){

            if(y!=0){
                ctx.fillText(-y/50,x,y);
            }
        }
    }

    function getRad(degree){
        return degree/180*Math.PI;
    }

    function cutShort(str,length){
        if(str.length>length){
            str=str.substr(0,length)+"...";
        }

        return str;
    }
//-->
</script>

在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线的更多相关文章

在笛卡尔坐标系上描绘函数 y=4x^2-2/4x-3
代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...
在笛卡尔坐标系上描绘函数(x*x+1)/(x*x-1)曲线
代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...
在笛卡尔坐标系上描绘函数2*x+Math.sqrt(5-x*x)及其共轭函数2*x-Math.sqrt(5-x*x)曲线
代码如下: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Ty ...
AcWing：112. 雷达设备（贪心 + 笛卡尔坐标系化区间）
假设海岸是一条无限长的直线,陆地位于海岸的一侧,海洋位于另外一侧. 每个小岛都位于海洋一侧的某个点上. 雷达装置均位于海岸线上,且雷达的监测范围为d,当小岛与某雷达的距离不超过d时,该小岛可以被雷达覆 ...
HTML5 Canvas 笛卡尔坐标系转换尝试
<!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type&quo ...
【python】列出http://www.cnblogs.com/xiandedanteng中所有博文的标题
代码: # 列出http://www.cnblogs.com/xiandedanteng中所有博文的标题 from bs4 import BeautifulSoup import requests u ...
使用R画地图数据
用R画地图数据首先,从这里下载中国地图的GIS数据,这是一个压缩包,完全解压后包含三个文件(bou2_4p.dbf.bou2_4p.shp和bou2_4p.shx),将这三个文件解压到同一个目录下. ...
hdu 4709 Herding hdu 2013 热身赛
题意:给出笛卡尔坐标系上 n 个点,n不大于100,求出这些点中能围出的最小面积. 可以肯定的是三个点围成的面积是最小的,然后就暴力枚举,计算任意三点围成的面积.刚开始是求出三边的长,然后求面积,运算 ...
hdu4419
对于这类面积覆盖的题,大致就两点要注意的 1.同一把矩形放在笛卡尔坐标系上做 2.pushup函数要注意下细节:及在统计子区间和之前要先判断是否有子区间用sum数组来保存区间被覆盖的情况,如果遇到多 ...

随机推荐

jquery请求解析xml
我们使用jque.ajax来做这个实验.其核心实现原理就是将请求回来的xml数据用$()选择器封装,然后进行傻瓜式操作. 代码如下: 需要注意的是请求数据格式要声明成:xml.不然不生效. $.aja ...
http中使用json封装数据的性能测试
http中使用json封装数据的性能测试一个项目使用json封装数据,接口例如: 客户端发送: POST /list.do HTTP/1.1 Host: zoomi.com.cn ...
二：Ionic Framework支持Android开发
首先安装ionic,在使用npm下载ionic和cordova的过程中有问题可以使用淘宝的npm镜像,具体的方法可以参考网络 npm install -g ionic cordova 其他还需要安装J ...
STL模板整理 list
介绍: list容器是一种序列式容器,它是STL实现的双向链表,与vector相比它可以实现快速的插入和删除,但是不能够快速的随机访问. 头文件: #include <list> 构造函数 ...
#1054 - Unknown column 'category' in 'field list'
导致这个问题的原因有: 1.确实没有这个字段 2.写错表了,你以为写到想要的表,没想到写到别处去了,当然没有这个字段了,这时候检查一下sql语句是不是选错了表,或者选错了数据库
派（Dispatch）
单派与多派 (Single Dispatch and Multi Dispatch) "检查一个数据项的类型,并据此去调用某个适当的过程称为基于类型的分派". 上面是来自<计 ...
EOJ Monthly 2018.8 D. Delivery Service-树上差分(边权/边覆盖)(边权转点权)(模板题)
D. Delivery Service 单测试点时限: 2.5 秒内存限制: 512 MB EOJ Delivery Service Company handles a massive amount ...
django 在python 3中提示无法找到 MySQLDB
一直百思不得其解,为什么会建立表失败,知道我看到了这个回答... I had luck with simply pip install mysqlclient in my python3.4 virt ...
STM32通用定时器实现LED灯闪烁
刚才看了一下STM32通用定时器的教程,其实和51的定时器使用差不多.只是因为32的时钟更复杂,可操控的寄存器更多,所以写的时候可能更复杂. 使用通用定时器中断的一般步骤:1.使能定时器时钟这个需要 ...
JZYZOJ1386 扑街状压dp
http://172.20.6.3/Problem_Show.asp?id=1386 有一个W行H列的街道,需要用1*2小砖铺盖,小砖之间互相不能重叠,问有多少种不同的铺法? 数组f的不往后延伸指 ...

在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线

在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线的更多相关文章

随机推荐

热门专题