[BZOJ2127]happiness-[网络流-最小割]

Description

传送门

Solution

按照最小割的思路考虑。

根据题意，当两个人都选文（理），需要砍掉两个人都选理（文）的加成；如果两个人选的不一样，就要都砍掉。

这是一个网络流建模的套路：

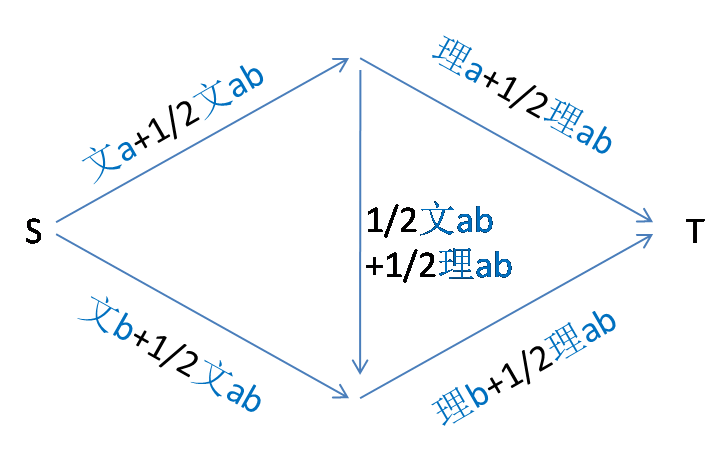
如图。为了防止出现分数，我们把每条边边权*2。

最后用总的喜悦值去掉网络流大小即可。（记得除以2）

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int inf=1e9;

int h[],tot=;
struct pas{int x,y,nxt,w,op,cost;}g[];
int dep[],S,T;
queue<int>q;
struct DINIC{
bool bfs()
{
    int x;
    memset(dep,,sizeof(dep));dep[S]=;
    while (!q.empty()) q.pop();
    q.push(S);
    while (!q.empty())
    {
        x=q.front();q.pop();
        for (int i=h[x];i;i=g[i].nxt)
        if (!dep[g[i].y]&&g[i].w)
        {
            dep[g[i].y]=dep[x]+;
            q.push(g[i].y);
            if (g[i].y==T) return ;
        }
    }
    return ;
}
int dfs(int x,int flow)
{
    if (x==T||(!flow))return flow;
    int temp=,js;
    for (int i=h[x];i;i=g[i].nxt)
    if (dep[g[i].y]==dep[x]+&&g[i].w)
    {
        js=dfs(g[i].y,min(flow,g[i].w));
        if (js)
        {
            g[i].w-=js;
            g[g[i].op].w+=js;
            temp+=js;
            flow-=js;
            if (!flow) return temp;
        }
    }
    if (!temp) dep[x]=;
    return temp;
}
    int dinic()
    {
        int ans=;
        while (bfs())
        ans+=dfs(S,inf);
        return ans;
    }
 }D;

void add(int x,int y,int w)
{
    g[++tot].x=x;g[tot].y=y;g[tot].w=w;g[tot].nxt=h[x];g[tot].op=tot+;h[x]=tot;
    g[++tot].x=y;g[tot].y=x;g[tot].w=;g[tot].nxt=h[y];g[tot].op=tot-;h[y]=tot;
}

int n,m,sum;
int art[][],sci[][];
int row_art[][],row_sci[][];
int col_art[][],col_sci[][];//col-column
int id(int x,int y){return (x-)*m+y;}
int main()
{
    scanf("%d%d",&n,&m);
    S=;T=id(n,m)+;
    for (int i=;i<=n;i++) for (int j=;j<=m;j++)
    {
        scanf("%d",&art[i][j]);    sum+=art[i][j];
        art[i][j]*=;
    }
    for (int i=;i<=n;i++) for (int j=;j<=m;j++)
    {
        scanf("%d",&sci[i][j]);    sum+=sci[i][j];
        sci[i][j]*=;
    }
    for (int i=;i<n;i++) for (int j=;j<=m;j++)
    {
        scanf("%d",&row_art[i][j]);sum+=row_art[i][j];
        art[i][j]+=row_art[i][j];
        art[i+][j]+=row_art[i][j];
    }
    for (int i=;i<n;i++) for (int j=;j<=m;j++)
    {
        scanf("%d",&row_sci[i][j]);sum+=row_sci[i][j];
        sci[i][j]+=row_sci[i][j];
        sci[i+][j]+=row_sci[i][j];
        add(id(i,j),id(i+,j),row_art[i][j]+row_sci[i][j]);
        add(id(i+,j),id(i,j),row_art[i][j]+row_sci[i][j]);
    }
    for (int i=;i<=n;i++) for (int j=;j<m;j++)
    {
        scanf("%d",&col_art[i][j]);sum+=col_art[i][j];
        art[i][j]+=col_art[i][j];
        art[i][j+]+=col_art[i][j];
    }
    for (int i=;i<=n;i++) for (int j=;j<m;j++)
    {
        scanf("%d",&col_sci[i][j]);sum+=col_sci[i][j];
        sci[i][j]+=col_sci[i][j];
        sci[i][j+]+=col_sci[i][j];
        add(id(i,j),id(i,j+),col_art[i][j]+col_sci[i][j]);
        add(id(i,j+),id(i,j),col_art[i][j]+col_sci[i][j]);
    }
    for (int i=;i<=n;i++) for (int j=;j<=m;j++)
    {
        add(S,id(i,j),art[i][j]);
        add(id(i,j),T,sci[i][j]);
    }
    printf("%d",(sum*-D.dinic())/);
}