Java算法——回溯法

回溯法
一种选优搜索法，又称试探法。利用试探性的方法，在包含问题所有解的解空间树中，将可能的结果搜索一遍，从而获得满足条件的解。搜索过程采用深度遍历策略，并随时判定结点是否满足条件要求，满足要求就继续向下搜索，若不满足要求则回溯到上一层，这种解决问题的方法称为回溯法。

回溯法解求解问题步骤

1. 针对给定问题，定义问题的解空间树；
2. 确定易于搜索的解空间结构；
3. 以深度优先方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索；
4. 用回溯法求解问题，重点是设计问题的解空间树，其解题过程则是深度遍历解空间树的过程。

解空间树
是依据待求解问题的特性，用树结构表示问题的解结构、用叶子表示问题所有可能的解的一棵树。

解空间树的形成过程
我们可以把求解问题的过程当作一系列的决定来考虑，回溯法对每一个决定都系统地分析所有可能的结果。而每一次决定即为解空间树中的一个分支结点，各种可能的结果便形成了各棵不同的子树，问题最终所有可能的解将展现在所有的叶子上。这便是解空间树的形成过程。

对解空间树的遍历可搜索到问题所有可能的解，因此，可获得满足要求的全部解，也可通过对所有解的比较选择获得最优解。

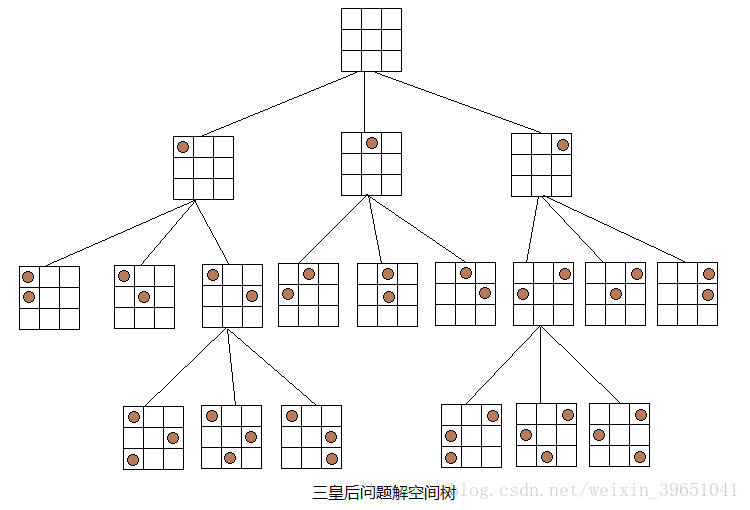
由于空间问题，下面给出一个三皇后问题的解空间树（3皇后问题无解），树中第i层的结点决定第i行皇后的摆放位置，均有三种不同的选择，便形成了三个孩子结点，但其中不包括不符合要求的布局。N皇后问题解空间树与三皇后问题解空间树类似。

求解N皇后问题的回溯法
N皇后问题要求求解在N*N的棋盘上放置N个皇后，并使各皇后彼此不受攻击的所有可能的棋盘布局。皇后彼此不受攻击的约束条件是：任何两个皇后均不能在棋盘上同一行、同一列或者同一对角线上出现。

由于N皇后问题不允许两个皇后在同一行，所以，可用一维数组X表示N皇后问题的解，X[i]表示第i行的皇后所在的列号。例如一个满足要求的四皇后棋盘布局如下图所示，其结果X数组的值为：[2， 4， 1， 3]。

由上述X数组求解N皇后问题，保障了任意两个皇后不在同一行上，而判定皇后彼此不受攻击的其他条件，可以描述如下：
（1）X[i] = X[s]，则第i行与第s行皇后在同一列上。
（2）如果第i行的皇后在第j列，第s行皇后在第t列，即X[i] = j和X[s] = t，则只要i-j = s-t或者i+j = s+t，说明两个皇后在同一对角线上。

对两个等式进行变换后，得到结论：只要|i-s| = |j-t|（即i-s = X[i]-X[s]），则皇后在同一对角线上。

解N皇后问题需要遍历解空间树，遍历中要随时判定当前结点棋盘布局是否符合要求，符合要求则继续向下遍历，直至判断得到一个满足约束条件的叶子结点，从而获得一个满足要求的棋盘布局；不符合要求的结点将被舍弃（称之为剪枝），并回溯到上一层的结点继续遍历。当整棵树遍历结束时，已获得所有满足要求的棋盘布局。

八皇后问题java实现：

public class Queen {
public static int num = 0; // 方案数
public static final int MAXQUEEN = 8; // 皇后数
public static int[] cols = new int[MAXQUEEN]; // 定义数组，表示MAXQUEEN列棋子中皇后摆放位置
/*
* @param n:填第n列的皇后
*/

public void getCount(int n) {
boolean[] rows = new boolean[MAXQUEEN];
for (int m = 0; m < n; m++) {
rows[cols[m]] = true;
int d = n - m;
// 正斜方向
if (cols[m] - d >= 0) {
rows[cols[m] - d] = true;
}
// 反斜方向
if (cols[m] + d <= (MAXQUEEN - 1)) {
rows[cols[m] + d] = true;
}
}
for (int i = 0; i < MAXQUEEN; i++) {
if (rows[i]) {
// 不能放
continue;
}
cols[n] = i;
// 下面仍然有合法位置
if (n < MAXQUEEN - 1) {
getCount(n + 1);
} else {
// 找到完整的一套方案
num++;
printQueen();
}
}
}

private void printQueen() {
System.out.println("第" + num + "种方案");
for (int i = 0; i < MAXQUEEN; i++) {
for (int j = 0; j < MAXQUEEN; j++) {
if (i == cols[j]) {
System.out.print("0 ");
} else {
System.out.print("+ ");
}
}
System.out.println();
}
}

public static void main(String[] args) {
Queen queen = new Queen();
queen.getCount(0);
}
}