Sklearn库例子3：分类——岭回归分类（Ridge Regression ）例子

为了解决数据的特征比样本点还多的情况，统计学家引入了岭回归。

岭回归通过施加一个惩罚系数的大小解决了一些普通最小二乘的问题。回归系数最大限度地减少了一个惩罚的误差平方和。

这里是一个复杂的参数，用来控制收缩量，其值越大，就有更大的收缩量，从而成为更强大的线性系数。

Ridge和Line_Model一样，用fit(x,y)来训练模型，回归系数保存在coef_成员中

例子：

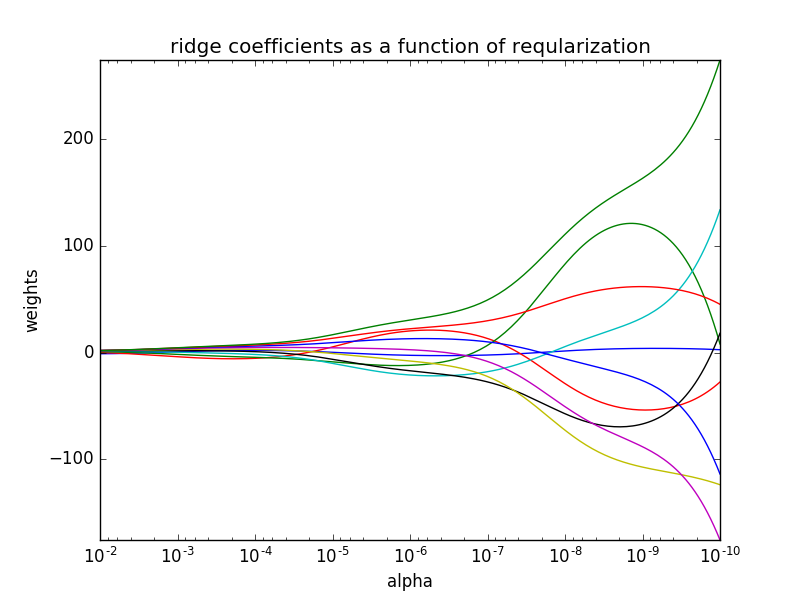
在这个例子使用岭回归作为估计器。结果中的每个颜色表示的系数向量的一个不同的功能，这是显示作为正则化参数的函数。在路径的最后，作为α趋于零和解决方案往往对普通最小二乘，系数表现出大的振荡。

代码如下：

#-*- encoding:utf-8 -*-
"""
岭回归example1
@Dylan
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

#x是10*10 的Hilbert 矩阵
x=1./(np.arange(1,11)+np.arange(0,10)[:,np.newaxis])
# print(x)
y=np.ones(10)

#####compute path
n_alphas=200
alphas=np.logspace(-10,-2,n_alphas)
# print(alphas)
clf=linear_model.Ridge(fit_intercept=False)
coefs=[]
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(x,y)
    coefs.append(clf.coef_)

###展示结果
ax=plt.gca()
ax.set_color_cycle(['b','r','g','c','k','y','m'])

ax.plot(alphas,coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('ridge coefficients as a function of reqularization')
plt.axis('tight')
plt.show()

其中 x为hilbert矩阵，生成方式值得借鉴。np.logspace()函数文档链接如下：here

结果如下：