扩展欧几里得求解同余方程（poj 1061）

设方程 ax + by = c , 若 gcd(a,b) 是 c的因子（记作gcd(a,b)|c）则方程有解，反之无解。

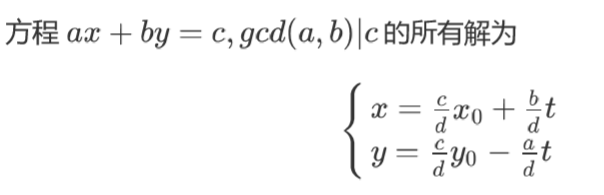
其中x0，y0是方程的一组特解 , d = gcd(a,b),

poj1061模型转化为（n-m)* t + L * k  = x - y  ，其中t和k是未知参数，形同ax+by = c 的形式，用extgcd即可求出x的一个特解，再通过这个特解找到x的最小正整数解就可以了。

AC代码:

#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long int
ll extgcd(ll a,ll b,ll& X,ll& Y){
	ll d = a;
	if(!b){
		X = 1;
		Y = 0;
	}
	else{
		d = extgcd(b,a%b,Y,X);
		Y -=a/b*X;
	}
	return d;
}
int main(){
	ll x,y,m,n,l,X,Y;
	while(~scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&l)){
		ll D = extgcd(n-m,l,X,Y);
		if((x-y)%D != 0){
			printf("Impossible\n");
			continue;
		}
		ll t = (x-y)/D;
		X*= t;
		l = l/D;
		printf("%lld\n",((X%l+l)%l));

	}
	return 0;
}