分布式事务 --- CAP 理论

本文部分来自参考资料！！半原创

概述

介绍CAP理论，并简单地证明了三存二的定论。

CAP 理论

1998年，加州大学的计算机科学家 Eric Brewer 提出，分布式系统有三个指标。分别为：

Consistency （一致性）
Availability （可用性）
Partition tolerance （分区容错性）

这三个元素不会同时满足。下图显示了现在许多分布式事务的实现具备的两方面的功能。

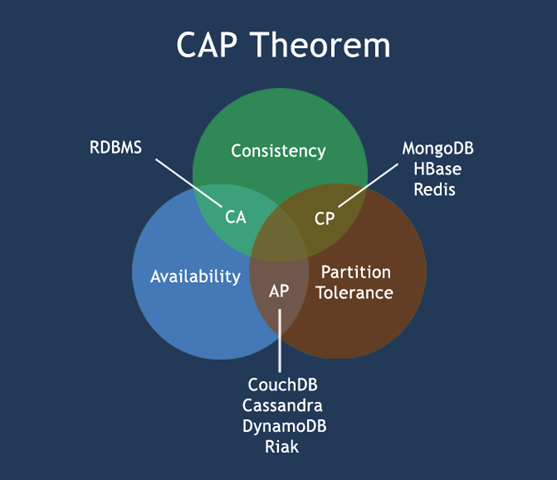
下面我们将介绍这三个元素，我们先来看一下一个简单的分布式系统。

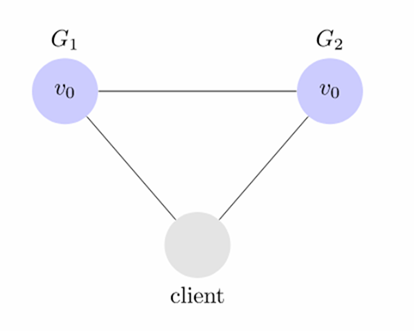
客户端连接着两台服务器，G1 和 G2 ，同时两个服务器都维护这一个 vo 的变量，客户端可以对服务端发起读写的功能。例如读

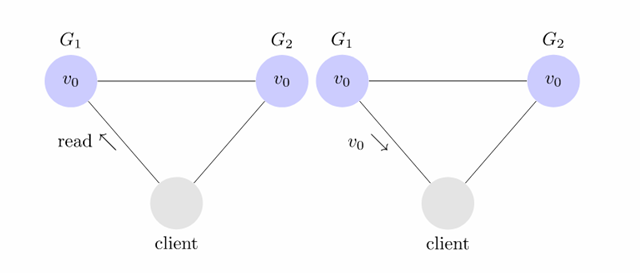
还有写：

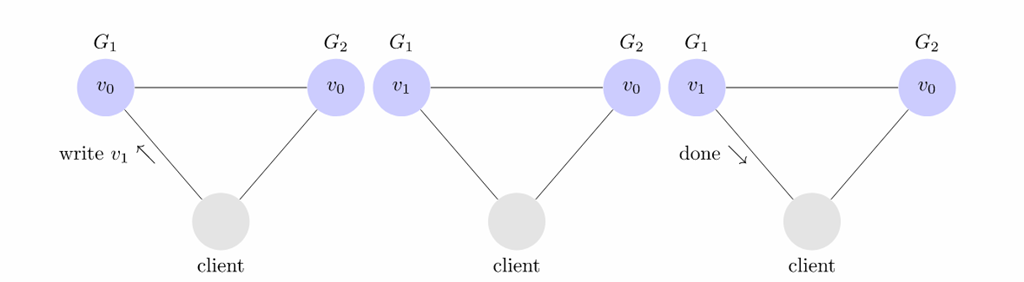
下面我们来了解三个原则。

分区容错

分区容错，具体的含义如下：

the network will be allowed to lose arbitrarily many messages sent from one node to another

阮老师的文章举了这样的例子。

大多数分布式系统都分布在多个子网络。每个子网络就叫做一个区（partition）。分区容错的意思是，区间通信可能失败。比如，一台服务器放在中国，另一台服务器放在美国，这就是两个区，它们之间可能无法通信。

分区容错的场景就像这样。

一致性

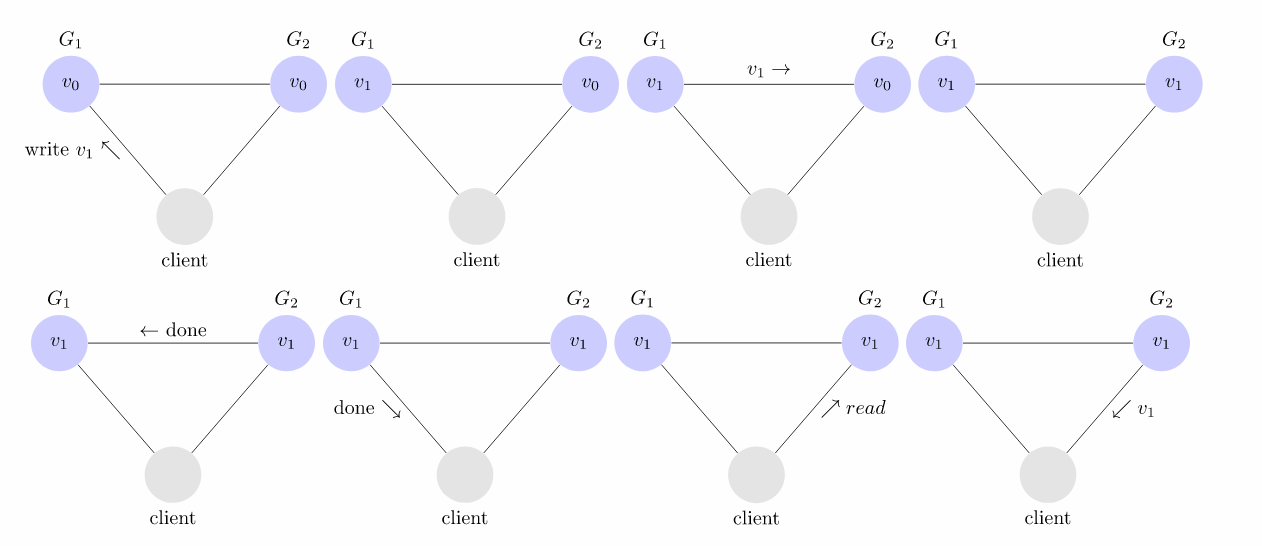
一致性很好理解，我们知道Mysql 的读写分离，很多情况下就是一个主库服务写操作，多个从库进行从同步，那么存在在向从库进行复制同步的过程的中，用户访问了从库，从而当初写进去的数值不一致，那么就没能保证一致性。下面是保证了一致性的情况。

可用性

只要收到用户的请求，服务器就必须给出回应。用户可以选择向 G1 或 G2 发起读操作。不管是哪台服务器，只要收到请求，就必须告诉用户，到底是 v0 还是 v1，否则就不满足可用性。

证明

证明的逻辑摘自阮一峰老师的文章，出处见参考文章

一致性和可用性，为什么不可能同时成立？答案很简单，因为可能通信失败（即出现分区容错）。

如果保证 G2 的一致性，那么 G1 必须在写操作时，锁定 G2 的读操作和写操作。只有数据同步后，才能重新开放读写。锁定期间，G2 不能读写，没有可用性不。

如果保证 G2 的可用性，那么势必不能锁定 G2，所以一致性不成立。

综上所述，G2 无法同时做到一致性和可用性。系统设计时只能选择一个目标。如果追求一致性，那么无法保证所有节点的可用性；如果追求所有节点的可用性，那就没法做到一致性。

多种情况

牺牲一致性

保留可用性和分区容错性，例如发布一张网页到 CDN，多个服务器有这张网页的副本。后来发现一个错误，需要更新网页，这时只能每个服务器都更新一遍。一般来说，网页的更新不是特别强调一致性。短时期内，一些用户拿到老版本，另一些用户拿到新版本，问题不会特别大。当然，所有人最终都会看到新版本。所以，这个场合就是可用性高于一致性。

牺牲可用性

保留一致性和分区容错性，从上面的证明我们也可以知道，为了保持一致性，一定是数据要求准确的场景，可以看到 MonoDB 和 redis 就是牺牲了可用性，从而保证了一致性和分区容错性。

牺牲分区可用性

放弃分区容错性，加强一致性和可用性，其实就是传统的单机数据库的选择。

总结

通过上面的学习我们知道了CAP 理论，知道了分布式事务中大部分情况下只能保证两个元素的存在，而由于网络延时等等原因，分区容错是客观地存在的，无法避免，所以人们更多地往一致性和可用性方面努力。

参考资料