机器学习（四）——Lasso线性回归预测构建分类模型（matlab）

Lasso线性回归（Least Absolute Shrinkage and Selection Operator）是一种能够进行特征选择和正则化的线性回归方法。其重要的思想是L1正则化：其基本原理为在损失函数中加上模型权重系数的绝对值，要想让模型的拟合效果比较好，就要使损失函数尽可能的小，因此这样会使很多权重变为0或者权重值变得尽可能小，这样通过减少权重、降低权重值的方法能够防止模型过拟合，增加模型的泛化能力。其中还有另外一种类似的方法叫做岭回归，其基本原理是在损失函数中加上含有模型权重系数的平方的惩罚项，其他原理基本相同。

Lasso线性回归的目标是最小化以下损失函数：



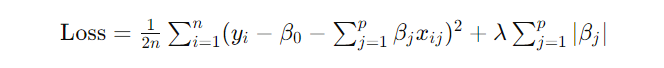
其中：



理论上来说当模型的损失函数越小时，构建的模型越接近真实分布，但是当模型的参数远远大于用来训练模型的数量的时候，很容易造成过拟合（模型学到的特征不是样本之间的共同特征，而是样本自身的特异性特征）。

通过L1正则化，可以约束线性模型中的权重系数，而且会减少特征量，保留权重系数有效的特征，同时能够减少系数之间的差距，让模型更具有泛化性。

当模型的损失函数达到最小的时候，惩罚项λ达到最优，模型的性能达到最优。

本文同样使用留一交叉验证的方法验证模型的分类性能，具体应用场景可以参考：机器学习（一）——递归特征消除法实现SVM（matlab）。

本文还提供了均方误差与特征数量的变化关系曲线、λ与均方误差的变化关系曲线以及分类结果的ROC曲线画法，如有需要请选择对应模块进行调整作图。

matlab实现代码如下：

labels = res(:, 1);  % 第一列是标签
features = res(:, 2:end);  % 后面的列是特征
features = zscore(features);   %归一化处理

%% 使用留一法交叉验证选择最优的 Lambda 值及其对应的特征
numSamples = size(features, 1);
lambda_values = logspace(-2, 2, 60); % 选择一系列 Lambda 值

mse_values = zeros(size(lambda_values)); % 存储每个 Lambda 值的均方误差
selected_features_all = cell(length(lambda_values), 1); % 存储每个 Lambda 值选择的特征

for i = 1:length(lambda_values)
    mse_fold = zeros(numSamples, 1);
    selected_feature = []; % 重置选择的特征

    for j = 1:numSamples
        % 划分训练集和验证集
        X_train = features([1:j-1, j+1:end], :); % 使用除了当前样本之外的所有样本作为训练集
        y_train = labels([1:j-1, j+1:end]); % 训练集标签
        X_valid = features(j, :); % 当前样本作为验证集
        y_valid = labels(j); % 验证集标签

        % 训练 LASSO 模型
        B = lasso(X_train, y_train, 'Lambda', lambda_values(i));

        % 在验证集上进行预测
        y_pred = X_valid * B;

        % 计算均方误差
        mse_fold(j) = mean((y_pred - y_valid).^2);

        % 将选择的特征添加到列表中
        selected_feature = [selected_feature; find(B ~= 0)]; % 使用分号进行垂直串联

    end

    % 计算当前 Lambda 值的平均均方误差
    mse_values(i) = mean(mse_fold);
   selected_feature= unique(selected_feature);%消除重复的特征
    % 保存每个 Lambda 值选择的特征
    selected_features_all{i} = selected_feature;
end

% 找到使均方误差最小的 Lambda 值

[min_mse, min_idx] = min(mse_values);
min_idx=min_idx-2;    %相当于当λ达到最优时，特征数量为0，所以要找最靠近最优λ的λ值来构建模型，此处可调
min_mse=mse_values(min_idx);
optimal_lambda = lambda_values(min_idx);

% 找到最优 Lambda 值对应的特征
selected_features_optimal = selected_features_all{min_idx};
selected_features_optimal = unique(selected_features_optimal);  %%%%%%%保留不同的特征，防止特征重复出现
% 显示最优的 Lambda 值及其对应的特征
disp(['最优的 Lambda 值：', num2str(optimal_lambda)]);

%% 对挑选出来的向量构建模型，并使用留一交叉验证计算其平均准确率

% 初始化变量来存储准确率
num_samples = size(features, 1);
accuracies = zeros(num_samples, 1);
Prediction_probability=zeros(num_samples, 1);%声明一个空数组用于储存预测的概率

% 遍历每个样本
for i = 1:num_samples
    % 留出第 i 个样本作为验证集，其余样本作为训练集
    X_train = features([1:i-1, i+1:end], selected_features_optimal); % 选择选出来的特征
    y_train = labels([1:i-1, i+1:end]);
    X_valid = features(i, selected_features_optimal);
    y_valid = labels(i);

    % 训练逻辑回归模型
    mdl = fitglm(X_train, y_train, 'Distribution', 'binomial', 'Link', 'logit');

    % 在验证集上进行预测
    y_pred = predict(mdl, X_valid);

    % 将预测概率转换为类别标签
    y_pred_label = round(y_pred);

    Prediction_probability(i)=y_pred;
    % 计算准确率
    accuracies(i) = (y_pred_label == y_valid);
end

% 计算平均准确率
average_accuracy = mean(accuracies);

% 显示平均准确率
disp(['平均准确率：', num2str(average_accuracy)]);

% 计算选取的特征个数
num_selected_features = cellfun(@length, selected_features_all);

% 绘制三维图像
figure;
plot3(lambda_values, mse_values, num_selected_features, 'b-', 'LineWidth', 2);
xlabel('λ值');
ylabel('均方误差');
zlabel('特征数量');
title('λ值与均方误差以及特征数量的变化关系');
grid on;

% 绘制 λ 和平均误差曲线
figure;
semilogx(lambda_values, mse_values, 'b-', 'LineWidth', 2);
xlabel('λ值');
ylabel('均方误差');
title('λ值与均方误差的变化关系');
grid on;

%计算ROC模型的相关参数
[fpr, tpr, thresholds] = perfcurve(labels, Prediction_probability, 1);

% 绘制 ROC 曲线
figure;
plot(fpr, tpr);
xlabel('假阳性率 (FPR)');
ylabel('真阳性率 (TPR)');
title('Lasso回归模型下ROC 曲线');

% 计算曲线下面积（AUC）
auc = trapz(fpr, tpr);
legend(['AUC = ' num2str(auc)]);

%%    统计每次迭代后选择的特征的，然后出一个排名，迭代过程中出现最多次的特征认为是可靠的特征

% 初始化一个空的结构数组
unique_elements_struct = struct('value', {}, 'count', {});

% 遍历每个单元格中的数组，统计每个元素出现的次数
for i = 1:numel(selected_features_all)
    current_array = selected_features_all{i};
    unique_elements = unique(current_array);
    for j = 1:numel(unique_elements)
        element = unique_elements(j);
        idx = find([unique_elements_struct.value] == element);
        if isempty(idx)
            % 如果元素不在结构数组中，则添加它
            unique_elements_struct(end+1).value = element;
            unique_elements_struct(end).count = sum(current_array == element);
        else
            % 否则更新该元素的计数
            unique_elements_struct(idx).count = unique_elements_struct(idx).count + sum(current_array == element);
        end
    end
end

% 按照出现次数进行降序排序
[~, sorted_indices] = sort([unique_elements_struct.count], 'descend');
unique_elements_struct = unique_elements_struct(sorted_indices);

% 显示结果
for i = 1:numel(unique_elements_struct)
    disp(['Element ', num2str(unique_elements_struct(i).value), ' appeared ', num2str(unique_elements_struct(i).count), ' times.']);
end