lca总结+树上差分

lca

lca简称最近公共祖先——简介在此，不过多赘述

这里主要写的是倍增算法，oi-wiki上用的是vector，由于本人不会，只会用链表，所以这里就放链表的代码了

例题

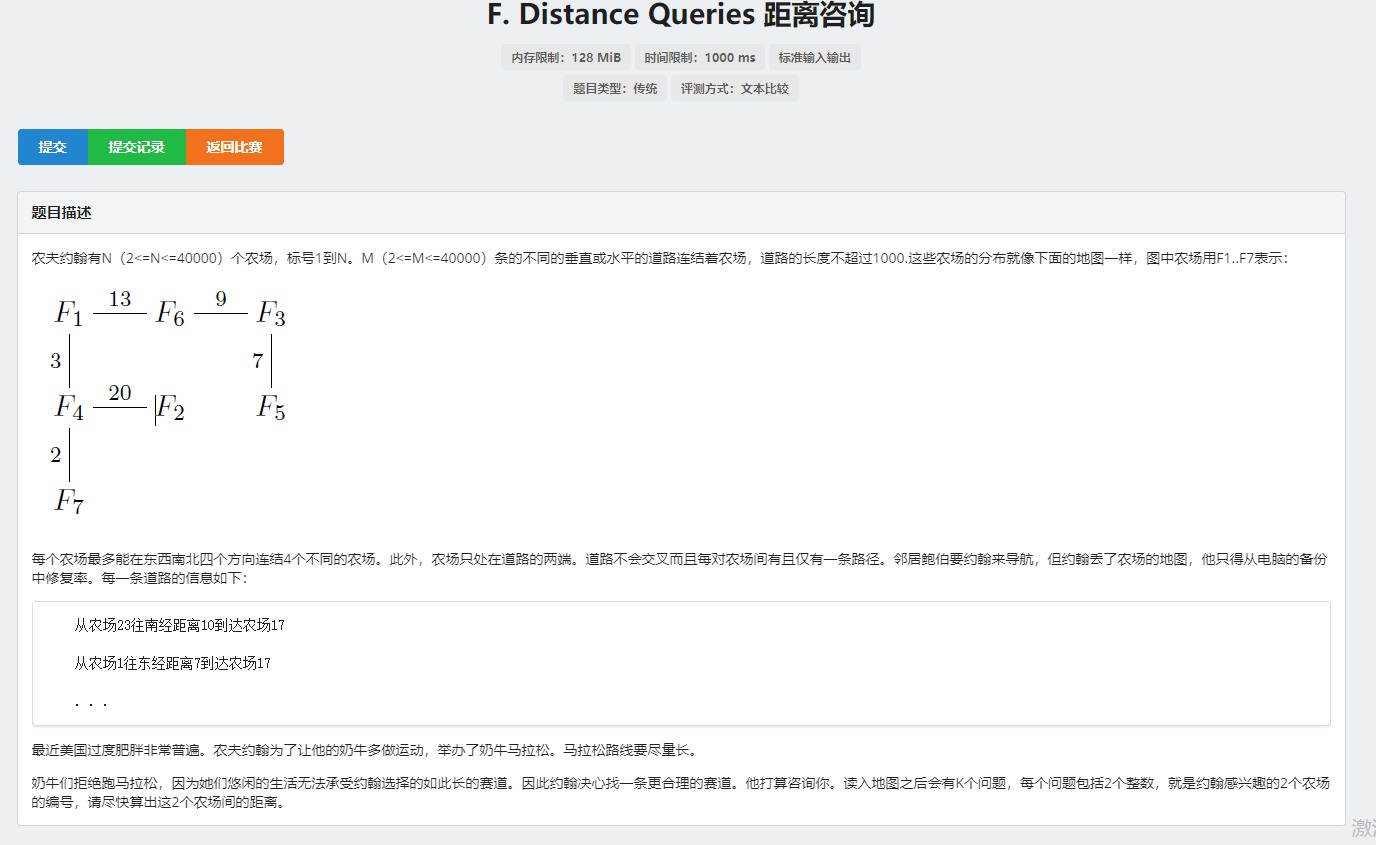
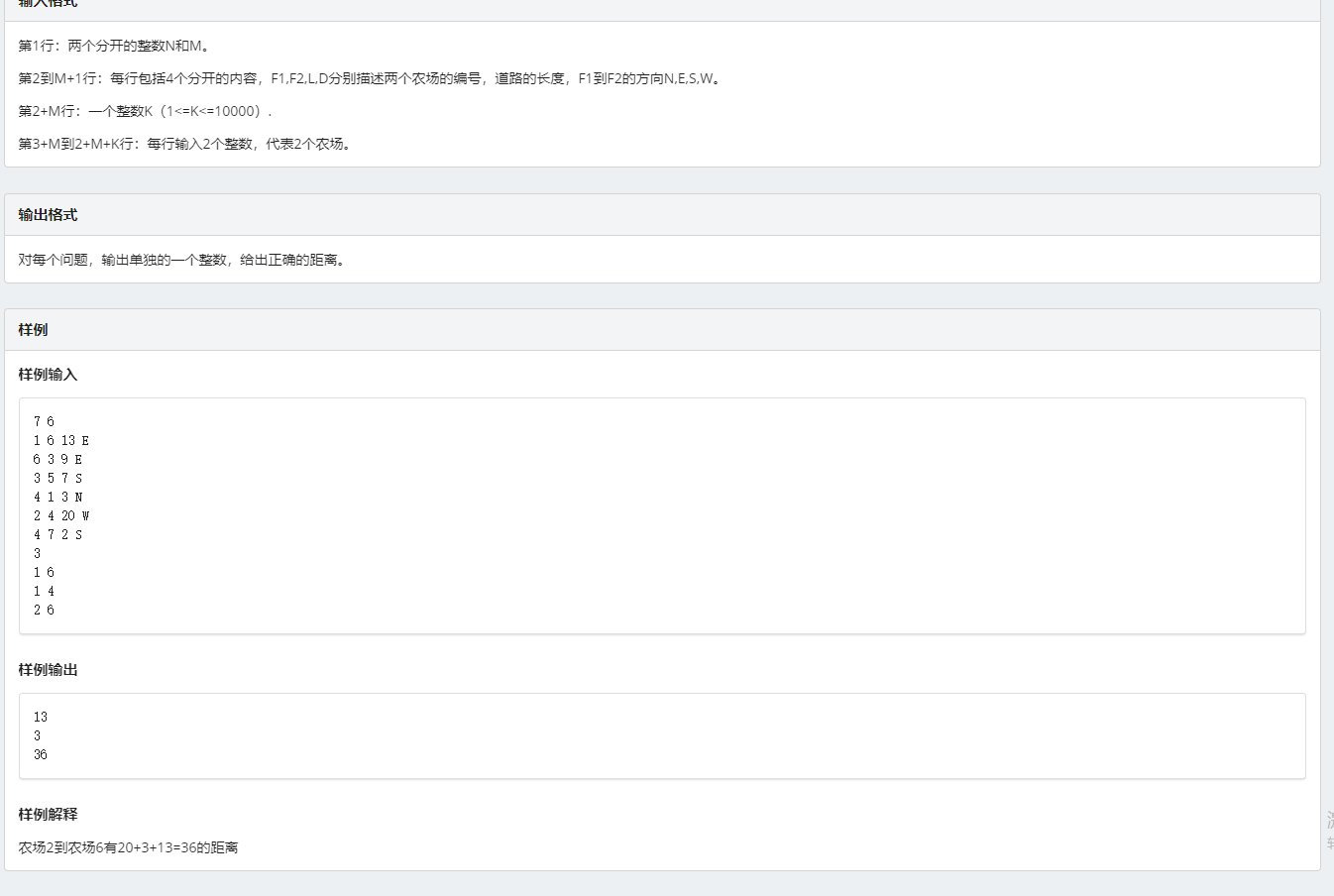
加一个数组按倍增数组的方式存距离即可

题解——点击查看代码

#include<bits/stdc++.h>
#define int long long
const int maxn=1e6+10;
using namespace std;
int n,m,root,nxt[maxn<<2],to[maxn<<2],head[maxn<<2],tot,val[maxn<<2];
int cnt,dep[maxn<<2],f[maxn][20],dis[maxn][20];
void add(int x,int y,int z)
{
	to[++tot]=y;
	val[tot]=z;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int u,int fa,int dist)
{
	dis[u][0]=dist;
	f[u][0]=fa;
	dep[u]=dep[fa]+1;
	for(int i=1;(1<<i)<=dep[u];i++)
	{
		f[u][i]=f[f[u][i-1]][i-1];
		dis[u][i]=dis[u][i-1]+dis[f[u][i-1]][i-1];
	}
	for(int i=head[u];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa) continue;
		dfs(y,u,val[i]);
	}
}
int lca(int x,int y)
{
	int res=0;
	if(dep[x]>dep[y]) swap(x,y);
	for(int i=17;i>=0;i--)
	{
		if(dep[x]+(1<<i)<=dep[y]) res+=dis[y][i],y=f[y][i];
	}
	if(x==y) return res;
	for(int i=17;i>=0;i--)
	{
		if(f[y][i]!=f[x][i])
		{
			res+=dis[x][i];
			res+=dis[y][i];
			x=f[x][i];
			y=f[y][i];
		}
	}
	return dis[x][0]+dis[y][0]+res;
}

signed main()
{
	scanf("%d%d",&n,&m);
	char aa[2];
	int x,y,z;
	for(int i=1;i<=m;i++)
	{
		scanf("%lld%lld%lld %s ",&x,&y,&z,&aa[1]);
		add(x,y,z);
		add(y,x,z);
	}
	dfs(1,0,0);
	int k;
	scanf("%lld",&k);
	for(int i=1;i<=k;i++)
	{
		scanf("%lld%lld",&x,&y);
		printf("%lld\n",lca(x,y));
	}

	return 0;
}

树上差分

主要用途是在树上的一些统计计数操作，对树上两点路径的操作用的

主要思想

dfs深搜实现，在两端结点计数，在深搜回溯时把计数的操作从子节点传递到父节点，用下面这个图理解一下

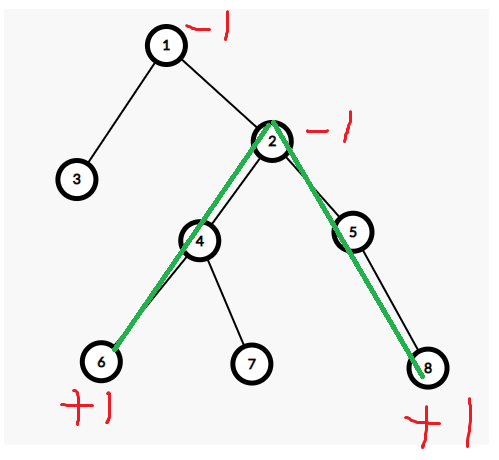
假设我们有这样一张图，我们要在6和8两个节点间的路径加一，那我们在用树上差分时，在两端+1，会发现它们的最近公共

祖先2及以上祖先都加了2，我们的目的是让2加1，2的祖先不变，则我们需要在2处减一，2的父亲处再减一即可

例题在此

题解

#include<bits/stdc++.h>
#define int long long
const int maxn=1e6+10;
using namespace std;
int n,m,root,head[maxn<<2],tot,sum;
int cnt,dep[maxn<<2],f[maxn][21],tg[maxn],a[maxn];
bool vis[maxn<<2];
struct tree{int to,val,nxt;}e[maxn<<2];
void add(int x,int y)
{
	e[++tot].to=y;
	e[tot].nxt=head[x];
	head[x]=tot;
}

void dfs1(int u,int fa)
{
	vis[u]=1;
	for(int i=1;(1<<i)<=dep[u];i++)
	{
		f[u][i]=f[f[u][i-1]][i-1];
	}
	for(int i=head[u];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(vis[y]||y==fa) continue;
		f[y][0]=u;
		dep[y]=dep[u]+1;
		dfs1(y,u);
	}
}

int lca(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
	{
		if(dep[x]>=dep[y]+(1<<i)) x=f[x][i];
	}
	if(x==y) return x;
	for(int i=20;i>=0;i--)
	{
		if(f[x][i]!=f[y][i])
		{
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];
}

void dfs(int u)
{
	vis[u]=1;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(vis[y])continue;
		dfs(y);
		tg[u]+=tg[y];
	}
}

signed main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
	}
	int x,y;
	for(int i=1;i<n;i++)
	{
		scanf("%lld%lld",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs1(1,0);
	for(int i=1;i<n;i++)
	{
		tg[a[i]]++;
		tg[a[i+1]]++;
		tg[ lca(a[i],a[i+1]) ]--;
		tg[f[ lca(a[i],a[i+1]) ][0]]--;
		/*
		en~~,神奇的东西，相邻的加1，但从a[2]到a[3]时a[2]不用加1，这就导致除了首尾糖果都 多加了1，但到最后一个糖果时不用拿，所以只有第一个位置的糖果是对的
		所以让第一个糖果数加1，最后输出时都减一就好了
		*/
	}
	memset(vis,0,sizeof vis);
	dfs(1);
	tg[a[1]]++;
	for(int i=1;i<=n;i++) printf("%lld\n",tg[i]-1);

	return 0;
}

---

你已完成新手教程，下面开启困难模式

书上差分计数变形

题目在此

题解——二分加树上差分

#include<bits/stdc++.h>
const int maxn=1e6+10;
using namespace std;
int n,m,root,head[maxn],tot,a[maxn],b[maxn];
int cnt,dep[maxn],f[maxn][21],dis[maxn][21],sum[maxn],l,r,ans;
bool vis[maxn];
struct tree{int to,val,nxt;}e[maxn<<2];
struct node{int a,b,anc,val;}le[maxn<<2]; 

void add(int x,int y,int z)
{
	e[++tot].to=y;
	e[tot].nxt=head[x];
	e[tot].val=z;
	head[x]=tot;
}

void dfs(int u,int fa)
{
	vis[u]=1;
	for(int i=1;(1<<i)<=dep[u];i++)
	{
		f[u][i]=f[f[u][i-1]][i-1];
		dis[u][i]=dis[u][i-1]+dis[f[u][i-1]][i-1];
	}
	for(int i=head[u];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(vis[y]||y==fa) continue;
		f[y][0]=u;
		b[y]=i;
		dis[y][0]=e[i].val;
		dep[y]=dep[u]+1;
		dfs(y,u);
	}
}

int lca(int x,int y)
{
	if(dep[x]>dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
	{
		if(dep[x]+(1<<i)<=dep[y]) y=f[y][i];
	}
	if(x==y) return y;
	for(int i=20;i>=0;i--)
	{
		if(f[y][i]!=f[x][i])
		{
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[y][0];
}

int solve(int x,int y)
{
	int res=0;
	if(dep[x]<dep[y])swap(x,y);
	for(int i=17;i>=0;i--)
	{
		if(dep[x]>=dep[y]+(1<<i)) res+=dis[x][i],x=f[x][i];
	}
	if(x==y)return res;
	for(int i=17;i>=0;i--)
	{
		if(f[y][i]!=f[x][i])
		{
			res+=dis[x][i]+dis[y][i];
			x=f[x][i];
			y=f[y][i];
		}
	}
	return dis[x][0]+dis[y][0]+res;
}

void update(int now,int fa)
{
	for(int i=head[now];i;i=e[i].nxt)
	{
		if(e[i].to!=fa)
		{
			update(e[i].to,now);
			sum[now]+=sum[e[i].to];
		}
	}
}

bool check(int x)
{
	int cnt=0,dec=0;
	memset(sum,0,sizeof sum);
	for(int i=1;i<=n;i++)
	{
		if(le[i].val>x)
		{
			cnt++;
			sum[le[i].a]++;
			sum[le[i].b]++;
			sum[le[i].anc]-=2;
			dec=max(dec,le[i].val-x);
		}
	}
	update(1,1);
	for(int i=1;i<=n;i++)
		if(sum[i]==cnt&&e[b[i]].val>=dec) return 1;
		return 0;
}

int main()
{
	scanf("%d%d",&n,&m);
	int x,y,z;
	for(int i=1;i<n;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
		add(y,x,z);
	}
	dfs(1,0);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		le[i]={x,y,lca(x,y),solve(x,y)};
		r=max(r,le[i].val);
	}
	r++;
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(check(mid))ans=r=mid;
		else l=mid+1;
	}
	printf("%d",ans);

	return 0;
}

树上差分加线段树合并

题目在此

题解

#include<bits/stdc++.h>
#define lid m[id].ls
#define rid m[id].rs
const int maxn=1e5+10;
using namespace std;
int n,t,len,head[maxn],nxt[maxn<<1],to[maxn<<1],tot,cnt;
int rt[maxn],sum,s[maxn*80],ans[maxn];
struct node{int ls,rs,sum;}m[maxn*80];
int dep[maxn],f[maxn][21];

inline void add(int x,int y)
{
	to[++cnt]=y;
	nxt[cnt]=head[x];
	head[x]=cnt;
}

inline void addm(int x,int y)
{
	add(x,y);
	add(y,x);
}

inline void push(int id)
{
	if(!lid){m[id].sum=m[rid].sum,s[id]=s[rid];return ;}
	if(!rid){m[id].sum=m[lid].sum,s[id]=s[lid];return ;}
	m[id].sum=max(m[lid].sum,m[rid].sum);
	s[id]=m[lid].sum>=m[rid].sum?s[lid]:s[rid];
}

inline void merge(int &a,int b,int l,int r)
{
    if(!b) return;
    if(!a){ a=b;return ;}
    if(l==r){ m[a].sum+=m[b].sum;return ;}
    int mid=(l+r)>>1;
    merge(m[a].ls,m[b].ls,l,mid),merge(m[a].rs,m[b].rs,mid+1,r);
    push(a);
}

inline void insert(int &id,int l,int r,int x,int y)
{
	if(!id)id=++tot;
	if(l==r)
	{
		m[id].sum+=y;
		s[id]=x;
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid)insert(lid,l,mid,x,y);
	else insert(rid,mid+1,r,x,y);
	push(id);
} 

inline void dfs(int u,int fa)
{
	for(int i=1;(1<<i)<=dep[u];i++)
		f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa)continue;
		f[y][0]=u;
		dep[y]=dep[u]+1;
		dfs(y,u);
	}
} 

inline int lca(int x,int y)
{
	if(dep[x]<dep[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[y]+(1<<i)<=dep[x])x=f[x][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
	{
		if(f[y][i]!=f[x][i])
		{
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];
}

void as(int u,int fa)
{
	for(int i=head[u];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa)continue;
		as(y,u);
		merge(rt[u],rt[y],1,maxn-10);
	}
	ans[u]=s[rt[u]];
	if(!m[rt[u]].sum) ans[u]=0;
}

int main(){
	scanf("%d%d",&n,&t);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		addm(x,y);
	}
	dfs(1,0);
	for(int i=1;i<=t;i++)
	{
		int a,b,c,d;
		scanf("%d%d%d",&a,&b,&c);
		d=lca(a,b);
		insert(rt[a],1,maxn,c,1),insert(rt[b],1,maxn,c,1);
		insert(rt[d],1,maxn,c,-1);
		insert(rt[f[d][0]],1,maxn,c,-1);
	}
	as(1,0);
	for(int i=1;i<=n;i++)
		printf("%d\n",ans[i]);
    return 0;
}