Perm 排列计数——Lucas&dfs

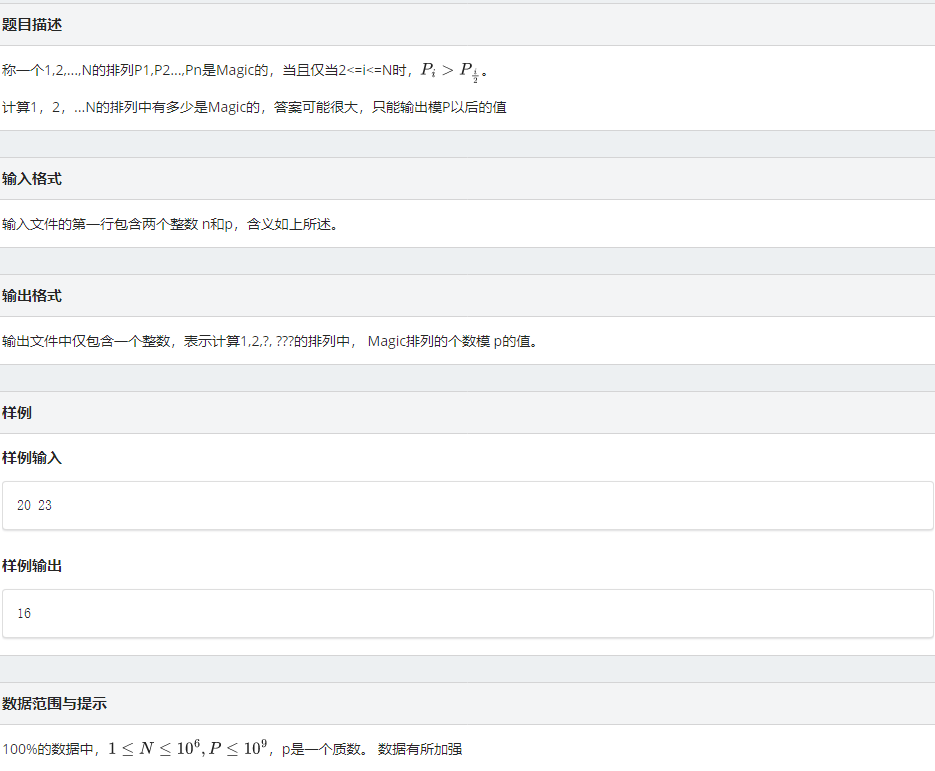
思路：这道题给出的公式看明白后即可得出正解，我们可以把他想象成一颗二叉树，任意一个点的任意一个子孙一直除以2后最终都会到达一终点，终点则为以该点为根的子树的最小值。

so——我们可以将根节点作为最后终点即最小值1，设有n个点，左子树选m个点，剩下的给右子树，左子树组合数即C(n-1,m)，and就可以得出转移式为f[father]=f[lson]*f[rson]*C(size[x]-1,size[2*x])  f表示满足条件的组合数，size表示以该点为根的树的大小

求大组合数再用Lucas定理就可以了

直接A了~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Damn：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=10000010;
int n,mod;
int ans[N],size[N];
int read(){
	int ans=0;bool f=0;char ch=getchar();
	while(ch<'0' || ch>'9'){if(ch=='-')f=1;ch=getchar();}
	while(ch>='0' && ch<='9'){ans=(ans<<1)+(ans<<3)+(48^ch);ch=getchar();}
	return f?-ans:ans;
}
int quickmi(int a,int k){
    int ans=1;
    while(k){
        if(k&1) ans=ans*a%mod;
        k>>=1;
        a=a*a%mod;
    }
    return ans;
}
int C(int x,int y){
	if(x<y) return 0;
	return ans[x]*quickmi(ans[y],mod-2)%mod*quickmi(ans[x-y],mod-2)%mod;
}
int lucas(int a,int b){
    if(a<mod&&b<mod) return C(a,b);
    return C(a%mod,b%mod)*lucas(a/mod,b/mod)%mod;
}
int dfs(int x){
    if(x>n)return 1;
    int lson=dfs(x*2),rson=dfs(x*2+1);
    size[x]=size[x*2]+size[x*2+1]+1;
    return ((lson*rson)%mod)*lucas(size[x]-1,size[x*2])%mod;
}
signed main(){
	n=read(),mod=read();
	ans[0]=ans[1]=1;
    for(int i=2;i<=n;i++) ans[i]=ans[i-1]*i%mod;
    printf("%lld",dfs(1));
    return 0;
}

#一名爱打篮球的oier#