HZNU-ACM寒假集训Day2小结 二分答案

Day2 ---二分

这里直接给出模板

两种对应不同的情况 可以借助数轴理解

int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> ;
        if (check(mid)) r = mid;
        else l = mid + ;
    }
    return l;
}

int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r +  >> ;
        if (check(mid)) l = mid;
        else r = mid - ;
    }
    return l;
}

补充：有时候可以借助STL的std::lower_bound()来找第一个大于等于你的值的数，std::upper_bound()来找第一个大于数所在的位置

P1873 砍树

int a[];
int n, m;
bool check(int k) {  //检查可行性，k为锯片高度
  long long sum = ;
  for (int i = ; i <= n; i++)       //检查每一棵树
    if (a[i] > k)                    //如果树高于锯片高度
      sum += (long long)(a[i] - k);  //累加树木长度
  return sum >= m;                   //如果满足最少长度代表可行
}
int find(int x) {
  int l = , r = ;  //因为是左闭右开的，所以10亿要加1
  while (l +  < r) {         //如果两点不相邻
    int mid = (l + r) / ;    //取中间值
    if (check(mid))           //如果可行
      l = mid;                //升高锯片高度
    else
      r = mid;  //否则降低锯片高度
  }
  return l;  //返回左边值
}
int main() {
  cin >> n >> m;
  for (int i = ; i <= n; i++) cin >> a[i];
  cout << find(m);
  return ;
}

实数二分 Pie http://poj.org/problem?id=3122

#include<iostream>
#include<string>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<queue>
#include<stack>
#include<sstream>
#include<cstdio>
const double eps = 1e-;
const int maxn = 1e6 + ;
const double PI = acos(-1.0);
typedef long long ll;
using namespace std;
double r[];
int n, k;
bool check(double x) {
    int cnt = ;
    for (int i = ; i < n; i++) {
        cnt+= (int)(r[i] / x);
    }
    if (cnt >= k+) return true;
    else return false;
}

int main() {
    std::ios::sync_with_stdio();
    cin.tie();
    double Max;
    int T;

    cin >> T;

    while (T--) {
        cin >> n >> k;
        Max = -;

        for (int i = ; i < n; i++) {
            cin >> r[i];
            r[i]=r[i]*r[i]*PI;
            Max = max(Max, r[i]);
        }
        double l = ;
        double r = Max+;
        while (r - l > eps) {
            double mid = (l + r) / ;
            if (check(mid)) {
                l = mid;
            }
            else r = mid;
        }
        printf("%.4f\n", l );

    }
    return ;
}

注意精度

三分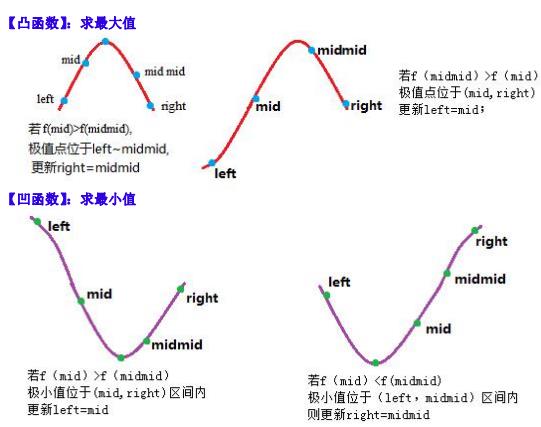 

  主要用于求函数极值

double f(double a){/*根据题目意思计算*/}
double three(double l,double r) //找凸点
{
    while(l<r-eps)
    {
        double mid=(l+r)/;
        double mmid=(mid+r)/;
        if(f(mid)>f(mmid)) r=mmid;
        else l=mid;
    }
    if(f(l)>f(r)) return l;
    else return r;
}

秦九韶算法从里到外逐层计算一次多项式

double    F(double x) {
    double sum = ;
    for (int i = n; i >= ; i--) {
        sum = sum * x + a[i];
    }
    return sum;
}