[UVALive 3661] Animal Run

图片加载可能有点慢，请跳过题面先看题解，谢谢

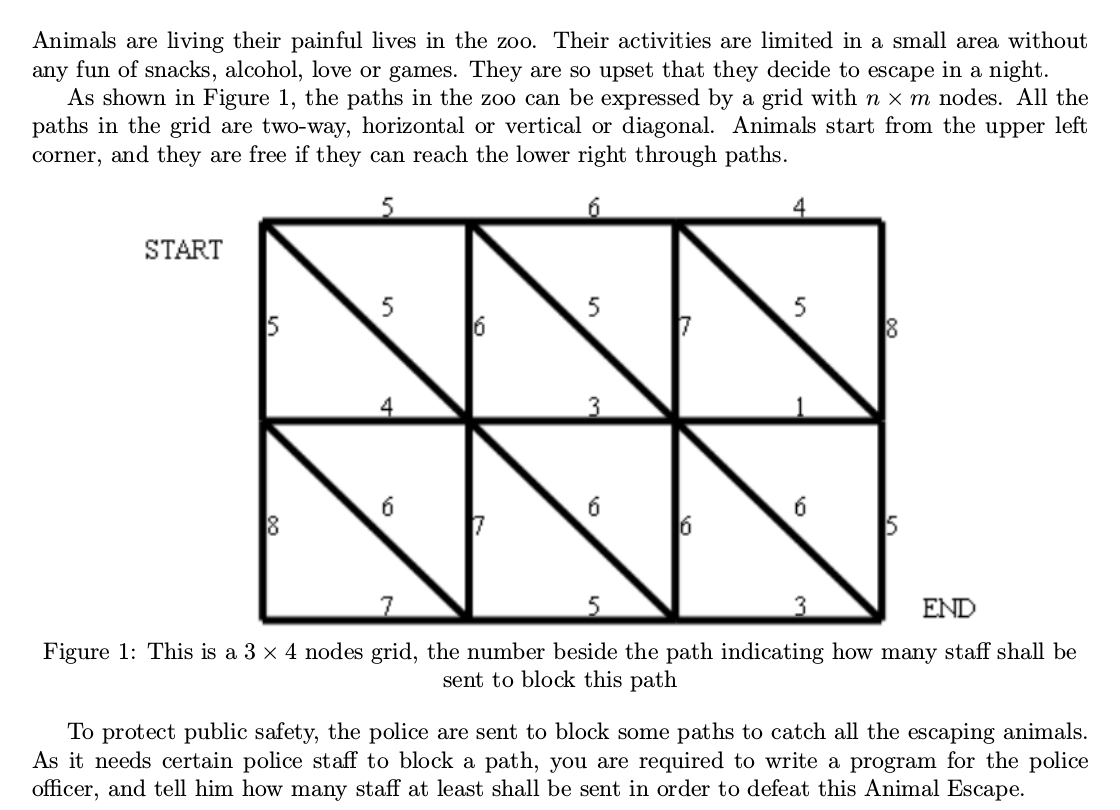
附：中文题面，[BZOJ1001]狼抓兔子
就要考联赛了，博客里题目的\(style\)都变了，几乎都是些套路啥的，这道题也比较套路
第一眼看这道题的感觉是网络流，求一个从左上角到右下角的最小割，但是点太多了，跑不过去
考虑这样一件事情：平面图转对偶图
最终的目的是要将左上角和右下角分开且代价最小，那就是求一条从左下到右上的最短路嘛
所以这里总结这样一个套路：平面图最小割\(--->\)对偶图最短路
那么这个对偶图怎么建？有两种建法：

1. 最浅显易懂的，直接将原网格的点作为新图的点，将原网格的边作为新图的边，然后跑最短路，时间上是没有什么问题的，可以跑过去，但是这样跑太慢了；
2. 考虑这样一种模型：将图中的三角形作为新图的点，新图中的边就是这些三角形间的公共边，这样建的话，点和边都在\(O(n*m)\)级别，跑起来会比上面那种方法快很多；

$
$
\(PS\)：在\(BZOJ\)上提交这道题需要特判\(n\)，\(m\)等于\(1\)的情况
$
$

//made by Hero_of_Someone
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
#define N (1010)
#define M (2000010)
#define il inline
#define RG register
using namespace std;
il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();
  if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }

int t,n,m,S,T,c[N][N][3];
int num,head[M],nxt[M*3],to[M*3],w[M*3];
il void add(int u,int v,int d){
  nxt[++num]=head[u];to[num]=v;w[num]=d;head[u]=num;
}

il int id(int x,int y,int z){return n*m*z+x*m+y+1;}

il void init(){
  S=0,T=2*n*m+2; num=0; memset(head,0,sizeof(head));
  for(RG int i=0;i<n;i++) for(RG int j=0;j<m-1;j++) c[i][j][0]=gi();
  for(RG int i=0;i<n-1;i++) for(RG int j=0;j<m;j++) c[i][j][1]=gi();
  for(RG int i=0;i<n-1;i++) for(RG int j=0;j<m-1;j++) c[i][j][2]=gi();
  for(RG int i=0;i<n-1;i++)
    for(RG int j=0;j<m-1;j++){
      int x=id(i,j,0);//左下角的三角形
      if(j) add(x,id(i,j-1,1),c[i][j][1]);
      if(i<n-1) add(x,id(i+1,j,1),c[i+1][j][0]);
      int y=id(i,j,1);//右上角的三角形
      if(i) add(y,id(i-1,j,0),c[i][j][0]);
      if(j<m-1) add(y,id(i,j+1,0),c[i][j+1][1]);
      add(x,y,c[i][j][2]); add(y,x,c[i][j][2]);
    }
  for(RG int i=0;i<n-1;i++) add(S,id(i,0,0),c[i][0][1]);
  for(RG int j=0;j<m-1;j++) add(S,id(n-2,j,0),c[n-1][j][0]);
  for(RG int i=0;i<n-1;i++) add(id(i,m-2,1),T,c[i][m-1][1]);
  for(RG int j=0;j<m-1;j++) add(id(0,j,1),T,c[0][j][0]);
}//设S为左下的起点，T为右上的起点

int dis[M];
bool vis[M];
struct node{int x,dis;
  bool operator<(const node& a)const{return dis>a.dis;}
};
priority_queue<node>que;
void Dij(){
  memset(vis,0,sizeof(vis));
  memset(dis,127/3,sizeof(dis));
  dis[0]=0; que.push((node){0,0});
  while(!que.empty()){
    int x=que.top().x; que.pop();
    if(vis[x]) continue;
    for(int i=head[x];i;i=nxt[i]){
      int v=to[i];
      if(dis[v]>dis[x]+w[i]){
    dis[v]=dis[x]+w[i];
    que.push((node){v,dis[v]});
      }
    }
    vis[x]=1;
  }
}

il void work(){ Dij(); printf("Case %d: Minimum = %d\n",++t,dis[T]); }

int main(){ while(scanf("%d%d",&n,&m)&&n){ init(); work(); } return 0; }