异常检测算法Robust Random Cut Forest（RRCF）关键定理引理证明

摘要：RRCF是亚马逊发表的一篇异常检测算法，是对周志华孤立森林的改进。但是相比孤立森林，具有更为扎实的理论基础。文章的理论论证相对较为晦涩，且没给出详细的证明过程。本文不对该算法进行详尽的描述，仅对其中的关键定理或引理进行证明。

Theorem 1:

对于点集S构成的树RCF(S)，假设S的bounding box的边长为P(S)，一次切分分离x1和x2的概率为。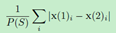

注意到，切分后，任意一边的bounding box的边长的减少量的期望值为，该期望值满足如下不等式：

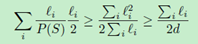
因此，每一次切分导致的新子集边长的减少量的期望值至少为。

（不等式的证明等价于证明算数均值≤均方根均值，因为f(x)=x²为凸函数，利用Jensen不等式可得）

Lemma 7：

（定义两点在树上的距离为：两点的最近共同祖先对应点集的bounding box的边长）

x1、x2的期望距离是：L1(x1,x2)*将x1,x2分离所需的期望步数。

证明：x1，x2在level S’被分离的概率为L1(x1,x2)/P(S’),因此在level S’被分离的期望距离为L1(x1,x2)/P(S’)*P(S’)= L1(x1,x2),如果经过n次（期望分割次数）分割将x1,x2分离，那么x1、x2的期望距离为：

E(x1,x2的距离)==n*L1(x1,x2)

因为每一次切分，将导致新的子集的边长至少减少1/2d，因此经过n次切分，边长最大为：

P(S)*(1-1/2d)ⁿ.

又边长不应小于L1(x1,x2)，因此：

P(S)*(1-1/2d)ⁿ≥L1(x1,x2)

两边取对数，得：

nlog(1-1/2d) ≥log(L1/P(S))

两边取相反数，得：

nlog(1+1/(2d-1))≤log(P(S)/L1)

考虑到lim_x->0log(1+x)=0,lim_x->0d(log(1+x))/dx=1，对不等式左侧作一阶泰勒展开：

log(1+1/(2d-1))=1/O(2d-1)

因此，分割次数n被O(d)*log(P(S)/L1)bound住，因此，两点在树上的距离被O(d)*log(P(S)/L1)* L1 bound住。

1范数和p范数的不等关系证明  ：

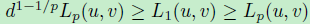
左侧不等式由Jensen不等式可得（f(x)=x^p在x≥0一侧是凸函数），右侧显然。

Lemma 9：

CODISP(x,Z,|S|)可以高效地计算。

证明：f(y, S, T) − f(y, S − C, T)不等于0的充要条件是，将包含y的节点的兄弟节点所构成的子树整棵全部删除（当然x也包含在这棵子树中）。因此，C的选择范围就变成了：从叶节点x到根节点的路径上的全部子树，而不再是从所有可能的组合中选择。