多元线性回归（Multivariate Linear Regression）简单应用

警告：本文为小白入门学习笔记

数据集：

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex3/ex3.html

由房屋的面积和bedroom个数影响房价的高低。

加载数据

x = load('ex3x.dat');
y = load('ex3y.dat');
m = length(y);
x = [ones(m, 1), x]; （之所以加上一列1，因为x1 = 1）；

看一下输入值，注意房间面积是卧室数量的1000倍左右。这种差异意味着预处理输入将显着提高梯度下降的效率。

在您的程序中，按标准偏差缩放两种类型的输入，并将其均值设置为零。

%数据处理，特征值缩放
sigma = std(x);%标准差
mu = mean(x); %平均数
x(:,2) = (x(:,2) - mu(2))./ sigma(2);
x(:,3) = (x(:,3) - mu(3))./ sigma(3);

假设函数任然是：

梯度下降算法：

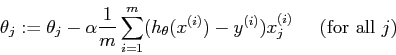
用居矩阵的方式计算：

theta = theta - x'*(x*theta-y)/m*a;

这里theta是一个3*1的矩阵，x是50*2矩阵，y是50*1矩阵，a表示alpha，m表示矩阵列长；

最终MATLAB程序是：

function [jVal] = multiLinerCost(a)
x = load('ex3x.dat');
y = load('ex3y.dat');
m = length(y);
x = [ones(m, 1), x];
%数据处理，特征值缩放
sigma = std(x);%标准差
mu = mean(x); %平均数
x(:,2) = (x(:,2) - mu(2))./ sigma(2);
x(:,3) = (x(:,3) - mu(3))./ sigma(3);

theta = zeros(size(x(1,:)))'; %3*1
J = zeros(50,1);
for iter = 1:50
theta = theta - x'*(x*theta-y)/m*a;
jVal = sum((x*theta-y).^2)/(2*m);
J(iter) = jVal;
end

%绘图
plot(0:49,J(1:50),'-');
xlabel('Number of iterations')
ylabel('Cost J')
end

控制台：

multiLinerCost(0.07) %选取学习速率（learning rates ）为0.07；

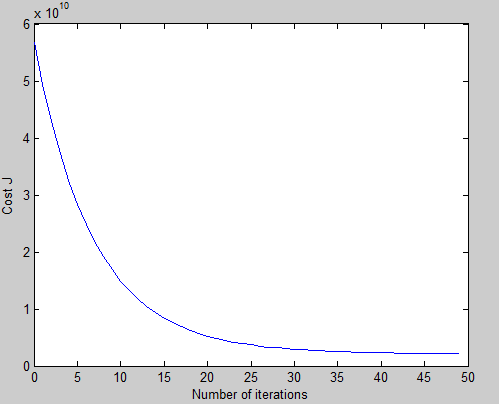
我们可以试试不同的learning rates 取值，对比曲线。

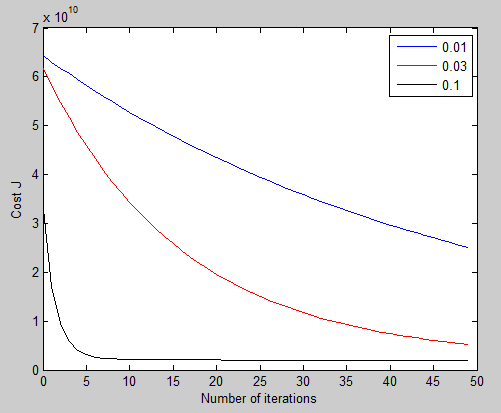
可以看到alpha =0.01时，曲线下降缓慢，迭代50次时还没有下降到最低值，alpha = 0.3时曲线在5附近急剧下降，在之后迭代就没有太大变化，所以选取0.07这个值相对合理。

如果alpha  再大会怎么样呢？

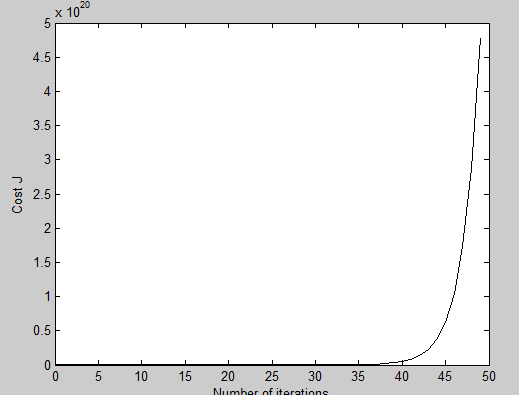
设alpha=1.5，可以看到这个值太大以至于一开始就为零，到最后趋近于无穷大。

所以一般取值 ：

使用梯度下降算法求得theta：

1.0e+05 *

3.4041
1.1063
-0.0665

使用矩阵计算求出：（如果用矩阵直接计算，不用特征值缩放）

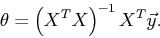
1.0e+04 *

8.9598
0.0139
-0.8738

(梯度下降法)所以最后的曲线方程是 h(x1,x2) = 340413 + 110631*x1 - 6650*x2

假如一个房间面积为1650，bedroom个数是3个，那么预测价格是$293,081；

这是对于二元线性回归问题，如果一般化X = [x1;x2;x3;........xn]  ;  theta = [theta0;theta1;......thetan]也可以解决。

这只是对多元线性回归的简单应用，还有很多东西要学习。

入门菜鸟，错误地方欢迎指教！