动态规划----最长公共子序列（C++实现）

最长公共子序列

• 题目描述：给定两个字符串s1 s2 … sn和t1 t2 … tm 。求出这两个字符串的最长公共子序列的长度。字符串s1 s2 … sn的子序列指可以表示为 … { i1 < i2 < … < ik }的序列。

• 输入样例

2
       asdf
       adfsd
       123abc
       abc123abc

• 输出样例

3

6

• 解题思路：

这道题是被称为最长公共子序列的问题（LCS，Longest Common Subsequence）的著名问题。这道题我们是用动态规划的思想来做的。我们先拿第一组测试用例，asdf 与 adfsd 作为例子来看一下这道题的思路。上图！！

j / i		1(a)	2(s)	3(d)	4(f)
1(a)
2(d)
3(f)
4(s)
5(d)

做这种题，我们要用一个二维数组（dp[MAX_N][MAX_N]）来存放每一个状态的值。如图所示，横向代表i、纵向代表j，那么，每一个网格的值是怎么来的呢。在这里我们把每一个状态即dp[i][j] 看做 s1 … si 和 t1 … tj 的LCS的长度。由此我们，s1 … s(i+1) 和 t1 … t(j+1) 对应的公共子列长度可能是：

当s(i+1) == t(j+1),在 s1 … si 和 t1 … tj 的公共子列末尾追加上s(i+1) 。

否则则可能是 s1 … si 和 t1 … t(j+1) 的公共子列或者 s1 … s(i+1) 和 t1 … tj 的公共子列最大值。

对应以下一个公式：

​

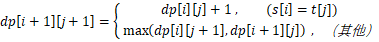
有了上面的公式我们就可以写代码了：

//最长公共子序列
#include<iostream>
#include<string>
#include<cstring>
#include<stdlib.h>
#define MAX 1001
using namespace std;
int dp[MAX][MAX];
int main()
{
	int N;
	cin >> N;
	while(N--)
	{
		string a,b;
		cin >> a >> b;
		memset(dp,0,sizeof(dp));
		int len_a=a.size(),len_b=b.size();
		for(int i=0;i<len_a;i++)
		{
			for(int j=0;j<len_b;j++)
			{
				if(a.at(i)==b.at(j))
					dp[i+1][j+1]=dp[i][j]+1;
				else
					dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1]);
			}
		}
		cout << dp[len_a][len_b] << endl;
		a.clear();
		b.clear();
	}
	return 0;
}