LA 3720 高速公路（互质判斜率）

https://vjudge.net/problem/UVALive-3720

题意：

有一个n行m列的点阵，问一共有多少条非水平非垂直的直线至少穿过其中的两个点。

思路:

没思路的题。

首先枚举矩形的大小，如果矩形的长宽互质，说明该斜率没出现过。

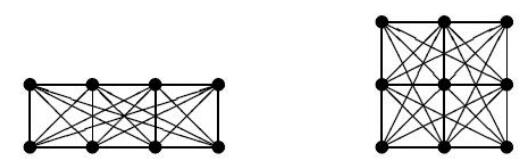
如图，1×1的矩阵的长宽互质，可以形成如图16条的直线（以1×1的矩阵为单位计算），但是如果放在整个矩阵来看，有些直线是可以合为一条直线的。

如果长宽gcd=2的话，说明该斜率的直线已经计算过了，我们要减去重复计算的。

如图，以2×2的矩阵为单位，减去1×1矩阵重复计算的直线，这样，135°斜率的直线一共有7条。

其它斜率的直线也是这样分析，详细见代码。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 using namespace std;

 const int maxn=+;

 int n,m;
 int g[maxn][maxn];

 int gcd(int a,int b)
 {
     return b==?a:gcd(b,a%b);
 }

 void init()
 {
     for(int i=;i<=;i++)
     for(int j=i;j<=;j++)
         g[i][j]=g[j][i]=gcd(j,i);
 }

 int main()
 {
     //freopen("D:\\input.txt","r",stdin);
     init();
     while(~scanf("%d%d",&n,&m) && n && m)
     {
         n--; m--;
         int ans=;
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=m;j++)
             {
                 int temp=(n-i+)*(m-j+);
                 if(g[i][j]==)  ans+=temp;
                 else if(g[i][j]==)  ans-=temp;
             }
         }
         printf("%d\n",*ans);
     }
     return ;
 }