exgcd模板
逆元模板P1082
#include <cstdio>
#include <algorithm> int exgcd(int a, int b, int &x, int &y) {
if(!b) {
x = ;
y = ;
return a;
}
int g = exgcd(b, a % b, x, y);
std::swap(x, y);
y -= (a / b) * x;
return g;
} int main() {
int a, b;
scanf("%d%d", &a, &b);
int x, y;
exgcd(a, b, x, y);
x = (x % b + b) % b;
printf("%d", x);
return ;
}
exgcd
注意exgcd不仅可以求解ax+by=gcd,还可以直接求解
ax+by=c(gcd|c)
代码:
LL Val;
LL mygcd(LL a, LL b, LL &x, LL &y) {
if(!b) {
x = Val / a;
y = ;
return a;
}
LL g = mygcd(b, a % b, x, y);
std::swap(x, y);
y -= (a / b) * x;
return g;
}
mygcd
但是有个缺点,就是跟上面比起来可能会爆long long而出错(屠龙勇士)
关于exgcd的推导过程:
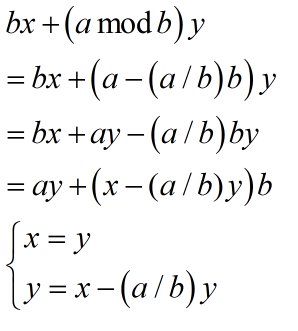
exgcd模板的更多相关文章
- poj 2115 C Looooops——exgcd模板
题目:http://poj.org/problem?id=2115 exgcd裸题.注意最后各种%b.注意打出正确的exgcd板子.就是别忘了/=g. #include<iostream> ...
- 扩展欧几里得(exgcd)与同余详解
exgcd入门以及同余基础 gcd,欧几里得的智慧结晶,信息竞赛的重要算法,数论的...(编不下去了 讲exgcd之前,我们先普及一下同余的性质: 若,那么 若,,且p1,p2互质, 有了这三个式子, ...
- 浅谈扩展欧几里得[exgcd] By cellur925
关于扩展欧几里得从寒假时就很迷,抄题解过了同余方程,但是原理并不理解. 今天终于把坑填上了qwq. 由于本人太菜,不会用markdown,所以这篇总结是手写的(什么).(字丑不要嫌弃嘛) ****** ...
- POJ 1061 青蛙的约会(扩展欧几里得)
根据题意,两个青蛙跳到同一个点上才算是遇到了,所以有 (x+m*t) - (y+n*t) = p * ll; (t是跳的次数,ll是a青蛙跳的圈数跟b青蛙的圈数之差.整个就是路程差等于纬度线周长的整 ...
- NOIP2012题解
NOIP2012题解 Day1 Vigenère 密码 vigenere 直接模拟就好了,对于那张表找找规律就很短了. #include<iostream> #include<cst ...
- POJ - 2115C Looooops 扩展欧几里得(做的少了无法一眼看出)
题目大意&&分析: for (variable = A; variable != B; variable += C) statement;这个循环式子表示a+c*n(n为整数)==b是 ...
- Noip前的大抱佛脚----Noip真题复习
Noip前的大抱佛脚----Noip真题复习 Tags: Noip前的大抱佛脚 Noip2010 题目不难,但是三个半小时的话要写四道题还是需要码力,不过按照现在的实力应该不出意外可以AK的. 机器翻 ...
- YBT 6 数学基础
$补+写题ing$ 第 1 章 快速幂 序列的第 k 个数 link $solution:$ 板子 A 的 B 次方 link $solution:$ 板子 [NOIP2013] 转圈游戏 link ...
- p1516&poj1061&bzoj1477 青蛙的约会
传送门(洛谷) 题目 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面.它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止.可是它们出发之前忘记了一件很重要的事情 ...
随机推荐
- go语言之行--网络编程、http处理流程详情
一.简介 go语言中的网络编程主要通过net包实现,net包提供了网络I/O接口,包括HTTP.TCP/IP.UDP.域名解析和Unix域socket等.和大多数语言一样go可以使用几行代码便可以启动 ...
- 20155211 Exp5 MSF基础应用
20155211 Exp5 MSF基础应用 基础问题回答 用自己的话解释什么是exploit,payload,encode? exploit:漏洞攻击.一个exploit程序肯定会触发系统的一个或多个 ...
- 【SP1812】LCS2 - Longest Common Substring II
[SP1812]LCS2 - Longest Common Substring II 题面 洛谷 题解 你首先得会做这题. 然后就其实就很简单了, 你在每一个状态\(i\)打一个标记\(f[i]\)表 ...
- 写个发邮件的功能php的(全代码)
---恢复内容开始--- 正好做了个项目,需要在线留言,一般在线留言发邮件是很常见的方式,一开始从网上搜了很久都没有很全的,也有全一点的,但是也不能用,运行不成功,下面给大家分享一下运行成功了的全部代 ...
- .NET Core容器化开发系列(零)——计划
.NET Core相当完善的跨平台特性以及其轻量化的底层接口为我们能顺畅进行微服务开发提供了非常棒的基础. 作为支撑微服务最常见的基础技术--容器化将是本系列的核心内容. 接下来我计划用一个月左右的时 ...
- Go实现Pow工作量证明
之前使用python编写了一段代码实现了工作量证明机制,近期由于参与以太坊智能合约开发钱包的工作接触到golang语言,所以借此以go来实现Pow(Proof of work). 实现代码如下: // ...
- 阿里云ubuntu16.04安装ruby
0x0 准备 环境:阿里云轻量服务器ubuntu16.04 目的:安装beef需要的ruby环境 更新软件 sudo apt-get update sudo apt-get upgrade sudo ...
- Daily Scrumming* 2015.12.16(Day 8)
一.团队scrum meeting照片 二.成员工作总结 姓名 任务ID 迁入记录 江昊 任务1036 https://github.com/buaaclubs-team/temp-front/com ...
- 《Linux内核设计与实现》第一、二章学习笔记
<Linux内核设计与实现>第一.二章学习笔记 姓名:王玮怡 学号:20135116 第一章 Linux内核简介 一.关于Unix ——一个支持抢占式多任务.多线程.虚拟内存.换页.动态 ...
- 【MOOC EXP】Linux内核分析实验一报告
程涵 原创博客 <Linux内核分析>MOOC课程http://mooc.study.163.com/course/USTC-1000029000 [反汇编一个简单的C程序] 实验 ...
