treap入门

这几天刚学了treap，听起来还行，就是调题调到恶心了……

就以这道题作为板子吧（”你本来也就做了一道题！”）

　　https://www.luogu.org/problemnew/show/P3369

先谈谈我对treap的理解

treap是一种二叉搜索树，二叉搜索树是这么一回事：
1.可以是一棵空树
2.若不空，那么左子树上所有节点的值都小于根节点的值，右子树上所有节点的值都大于根节点的值
3.左右子树分别为一棵二叉搜索树

treap是由tree和heap组合而来的，可见他还满足堆的性质。
通过随机一个额外的数值作为优先级，来构成一个堆。可以证明，随机顺序建立的二叉排序树的期望高度是O(logn)(虽然我不会证)，所以我认为，之所以用这个随机值，就是为了防止树退化成一个链的情况，导致时间复杂度变大

treap最重要也是最基础的操作是旋转，分为左右旋，为什么要有旋转呢？拿插入举例，插入一个节点当然是先根据二叉搜索树的性质插入到该插入的叶节点，
但是为了防止其退化成一条链，我们就需要通过旋转操作使该节点的优先级满足堆的性质。
总结一下，旋转操作是为了在符合二叉搜索树的前提下，让树满足堆的性质。
那具体怎么转呢？由上文可知，改变两个节点的父子关系的同时，还有满足二叉搜索树的性质，即旋转不影响二叉搜索树的性质。
直接上图：

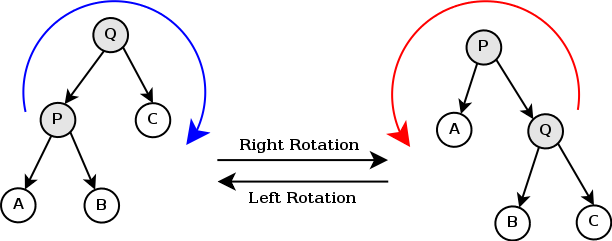
（感谢hzh巨佬的图）

从图中可以很直观的看出，通过右旋改变了左孩子和根节点的父子关系，通过右旋改变了右孩子和根节点的关系。
而且可以验证，这么做二叉搜索树的性质并没有改变。
于是左右旋的代码就可以模拟出来

 void right_rotate(int& Q)
 {
     int P = lson[Q];
     lson[Q] = rson[P];            //这个和下面那句不能反
     rson[P] = Q;
     update(Q); update(P);
     Q = P;
 }
 void left_rotate(int& Q)
 {
     int P = rson[Q];
     rson[Q] = lson[P];
     lson[P] = Q;
     update(Q); update(P);
     Q = P;
 }

其中update函数用来维护该节点储存的信息，比如字数大小，该节点深度

那咱们现在看看题吧。

对了，我维护的是小根堆，大根堆也应该是一样的吧，没试过

先说一下变量含义：

 int n, root = ;                //n种操作;root记录根节点是谁（因为进行某一操作后，根节点可能改变，所以要随时记录）
 int cnt = , lson[maxn], rson[maxn];    //cnt:节点总数（即每一个节点的编号）;lson[now],rson[now]:节点now的左右孩子
 int val[maxn], ran[maxn], size[maxn], Cnt[maxn];    //val[now]:节点now的权值;ran[now]:随机出来的优先级;size[now]:子树大小;
4　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //Cnt[now]记录和val[now]相同的节点多少个（用来处理数字重复） 

第一种操作是插入。上文已述，插入是先按二叉搜索树的性质插入到叶节点，在通过旋转满足堆的性质

 void insert(int& now, int v)
 {
     if(!now)                //找到要插入的叶节点了
     {
         now = ++cnt;        //新建节点
         val[now] = v;
         size[now] = Cnt[now] = ;
         ran[now] = rand();    //随机优先级
         return;
     }
     if(val[now] == v) Cnt[now]++;    //若树中已经有了该数，就直接Cnt[]++了
     else if(val[now] > v)        //说明在左子树
     {
         insert(lson[now], v);    //递归寻找
         if(ran[lson[now]] < ran[now]) right_rotate(now);
         //这一步放在了递归后面，说明此时节点已经插入好了（而且只是修改了左子树），那就判断并通过旋转维护堆
     }
     else
     {
         insert(rson[now], v);
         if(ran[rson[now]] < ran[now]) left_rotate(now);
     }
     update(now);
 }

第二种操作是删除。这咋办呢？如果找到后直接删除该点，那么他子树们就不知道该去哪儿了，显然乱套。
那怎么办呢，别忘了，旋转可以改变两个节点的父子关系，而仍不破坏这棵树，所以我们就可已找到他后，将他旋转下去直到叶节点，这时候再删除，就没什么关系了

 void del(int& now, int v)
 {
     if(!now) return;
     if(val[now] == v)    //找到了该数
     {
         if(Cnt[now] > ) //有重复
         {
             Cnt[now]--;
             update(now); return;
         }
         else if(lson[now] && rson[now])    //并没有旋转到根节点
         {
             left_rotate(now);     //只要选任意一棵子树旋转就行
             del(lson[now], v);    //这两句等价于right_rotate(now); del(rson[now], v);
         }
         else                //代表只剩一个孩子了，那么就直接用他的孩子代替他，相当于把他删除
         {
             now = lson[now] | rson[now];    //等价于now = lson[now] ? lson[now] : rson[now]
             update(now); return;
         }
     }
     else if(val[now] > v) del(lson[now], v);        //没找到就接着找
     else del(rson[now], v);
     update(now);
 }

第三种操作是查询排名，size[]就派上用场了。这跟线段树的查询第k小很像，就是查询到右子树时别忘加上左子树的大小和该点的重复个数

 int Find_id(int now, int v)
 {
     if(!now) return ;
     if(val[now] == v) return size[lson[now]] + ;        //别忘加上自己
     if(val[now] > v) return Find_id(lson[now], v);
     else return Find_id(rson[now], v) + size[lson[now]] + Cnt[now];
 }

第四种操作是查询排名为x的数，和操作3逻辑上很想，只不过有些步骤相反，还是看代码和注释比较直观

 int Find_num(int now, int id)
 {
     if(!now) return INF;
     if(size[lson[now]] >= id) return Find_num(lson[now], id);        //在左子树
     else if(id <= size[lson[now]] + Cnt[now]) return val[now];        //在左子树和自己，但因为左子树的已经走上面的语句了，就指自己
     else return Find_num(rson[now], id - size[lson[now]] - Cnt[now]);    //右子树，别忘减去（跟线段树找第k小挺像）
 }

第五种操作是查询x的前驱。首先如果当前节点的权值比v大，那么很显然应该去左子树中找；如果当前节点的权值比v小，说明v的前驱在左子树或者当前节点就是他的前驱，但因为当前节点的左子树的右子树中（没绕，没绕）也可能存在v的前驱，所以就要在这两者之中取max，具体看代码吧

 int Pre(int now, int v)
 {
     if(!now) return -INF;
     if(val[now] < v) return max(val[now], Pre(rson[now], v));    //前驱在右子树或是当前节点
     else return Pre(lson[now], v);
 }

前驱都会了，那后继还会远吗？　　　　　　--雪mrclr莱

 int Nex(int now, int v)
 {
     if(!now) return INF;    //相当于停止搜索和比较
     if(val[now] > v) return min(val[now], Nex(lson[now], v));
     else return Nex(rson[now], v);
 }

总算写完了，发一下完整代码

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #include<cctype>
 using namespace std;
 #define enter printf("\n")
 #define space printf(" ")
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn = 1e5 + ;
 inline ll read()
 {
     ll ans = ;
     char ch = getchar(), last = ' ';
     while(!isdigit(ch)) {last = ch; ch = getchar();}
     while(isdigit(ch))
     {
         ans = ans *  + ch - ''; ch = getchar();
     }
     if(last == '-') ans = -ans;
     return ans;
 }
 inline void write(ll x)
 {
     if(x < ) x = -x, putchar('-');
     if(x >= ) write(x / );
     putchar('' + x % );
 }

 int n, root = ;
 int cnt = , lson[maxn], rson[maxn];
 int val[maxn], ran[maxn], size[maxn], Cnt[maxn];
 void update(int now)
 {
     if(!now) return;
     size[now] = size[lson[now]] + size[rson[now]] + Cnt[now];
 }
 void right_rotate(int& Q)
 {
     int P = lson[Q];
     lson[Q] = rson[P];
     rson[P] = Q;
     update(Q); update(P);
     Q = P;
 }
 void left_rotate(int& Q)
 {
     int P = rson[Q];
     rson[Q] = lson[P];
     lson[P] = Q;
     update(Q); update(P);
     Q = P;
 }
 void insert(int& now, int v)
 {
     if(!now)
     {
         now = ++cnt;
         val[now] = v;
         size[now] = Cnt[now] = ;
         ran[now] = rand();
         return;
     }
     if(val[now] == v) Cnt[now]++;
     else if(val[now] > v)
     {
         insert(lson[now], v);
         if(ran[lson[now]] < ran[now]) right_rotate(now);
     }
     else
     {
         insert(rson[now], v);
         if(ran[rson[now]] < ran[now]) left_rotate(now);
     }
     update(now);
 }
 void del(int& now, int v)
 {
     if(!now) return;
     if(val[now] == v)
     {
         if(Cnt[now] > )
         {
             Cnt[now]--;
             update(now); return;
         }
         else if(lson[now] && rson[now])
         {
             left_rotate(now);
             del(lson[now], v);
         }
         else
         {
             now = lson[now] | rson[now];
             update(now); return;
         }
     }
     else if(val[now] > v) del(lson[now], v);
     else del(rson[now], v);
     update(now);
 }
 int Find_id(int now, int v)
 {
     if(!now) return ;
     if(val[now] == v) return size[lson[now]] + ;
     if(val[now] > v) return Find_id(lson[now], v);
     else return Find_id(rson[now], v) + size[lson[now]] + Cnt[now];
 }
 int Find_num(int now, int id)
 {
     if(!now) return INF;
     if(size[lson[now]] >= id) return Find_num(lson[now], id);
     else if(id <= size[lson[now]] + Cnt[now]) return val[now];
     else return Find_num(rson[now], id - size[lson[now]] - Cnt[now]);
 }
 int Pre(int now, int v)
 {
     if(!now) return -INF;
     if(val[now] < v) return max(val[now], Pre(rson[now], v));
     else return Pre(lson[now], v);
 }
 int Nex(int now, int v)
 {
     if(!now) return INF;
     if(val[now] > v) return min(val[now], Nex(lson[now], v));
     else return Nex(rson[now], v);
 }

 int main()
 {
     n = read();
     while(n--)
     {
         int d = read(), x = read();
         if(d == ) insert(root, x);
         else if(d == ) del(root, x);
         else if(d == ) {write(Find_id(root, x)); enter;}
         else if(d == ) {write(Find_num(root, x)); enter;}
         else if(d == ) {write(Pre(root, x)); enter;}
         else {write(Nex(root, x)); enter;}
     }
     return ;
 }

彩蛋：找名次写错了能MLE……求大佬解答……