字符串类——KMP子串查找算法

1， 如何在目标字符串 s 中，查找是否存在子串 p（本文代码已集成到字符串类——字符串类的创建（上）中，这里讲述KMP实现原理） ？

1，朴素算法：

　　2，朴素解法的问题：

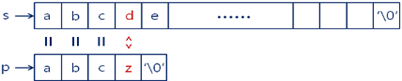
1，问题：有时候右移一位是没有意义的；

2，KMP 算法可以右移一定的位数，提高效率；

　　　　3，朴素算法和 KMP 算法对比示例图：

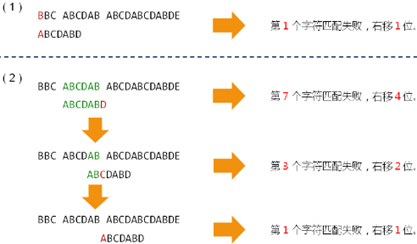
2，伟大的发现（KMP）：

1，匹配失败时的右移位数与子串本身相关，与目标无关；

2，移动位数 = 已匹配的字符数 - 对应的部分匹配值；

1，“已匹配的字符数”已知，“对应的部分匹配值”未知；

（2），部分匹配值就是对应元素和从开始元素开始连续相同的个数；

3，任意子串都存在一个唯一的部分匹配值；

3，部分匹配表示例：

4，部分匹配表如何获得 ？

1，前缀集：

1，除了最后一个字符外，一个字符串的全部头部组合；

2，后缀集：

1，除了第一个字符以外，一个字符串的全部尾部组合；

3，部分匹配值：

1，前缀集和后缀集最长共有元素的长度；

（2），得到共有长度是为了得到对应各个位置前面不相同的元素个数，这样如果前面不同元素匹配了，那么就可以直接移动的了；

4，ABCDABD 部分匹配表示例：

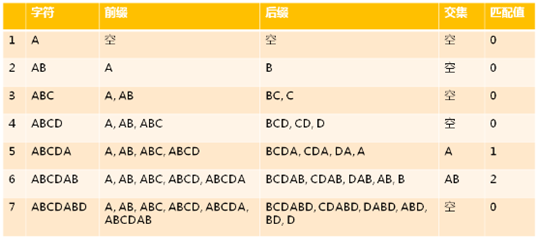
5，怎么编程产生部分匹配表（Partial Matched Table）（递推完成）？

1，实现关键：

1，PMT[1] = 0（下标为 0 的元素匹配值为 0）；

2，从 2 个字符开始递推（从下标为 1 的字符开始递推）；

3，假设 PMT[n] = PMT[n-1] + 1（最长共有元素的长度）（这是一个贪心假设）；

4，当假设不成立，PMT[n] 在 PMT[n-1]（这里是指的第 PMT[n-1] 个元素）个元素的 ll 值上用种子作为扩展的基础上继续比对；

1，当当前前子集“前后集最长共有元素数”为 0 时，说明其元素都不相等，可以直接比较当前子集延长一字母序列的首尾字母，且此子集“前后集最长共有元素数”最大为 1；

2，将 “前后集最长共有元素数”对应的前后缀最为种子扩展；

3，假设不成立时，把已经匹配的前 PMT[n-1] 个元素的“前后集最长共有元素数”（因为必须在相同的位置上扩展才有意义）作为种子来扩展；

6，部分匹配表的递推与实现：

　　1，部分匹配表的递推：

　　2，在 String 中实现部分匹配表：

 /* 建立指定字符串的 pmt（部分匹配表）表 */
 int* String::make_pmt(const char* p)  //  O(m)，只有一个 for 循环
 {
     int len = strlen(p);
 int* ret = static_cast<int*>(malloc(sizeof(int) * len));

     if ( ret != NULL )
     {
         int ll = ; //定义 ll，前缀和后缀交集的最大长度数，largest length;第一步
         ret[] = ;  // 长度为 1 的字符串前后集都为空，对应 ll 为 0；

         for(int i=; i<len; i++)  // 从第一个下标，也就是第二个字符开始计算，因为第 0 个字符前面已经计算过了； 第二步
         {
             /* 算法第四步 */
             while( (ll > ) && (p[ll] != p[i]) ) // 当 ll 值为零时，转到下面 if() 函数继续判断，最后赋值与匹配表，所以顺序不要错；
             {
                 ll = ret[ll - ];  // 从之前匹配的部分匹配值表中，继续和最后扩展的那个字符匹配
             }

             /* 算法的第三步，这是成功的情况 */
             if( p[ll] == p[i] ) // 根据 ll 来确定扩展的种子个数为 ll，而数组 ll 处就处对应的扩展元素，然后和最新扩展的元素比较；
             {
                 ll++;   // 若相同（与假设符合）则加一
             }

             ret[i] = ll;   // 部分匹配表里存储部分匹配值 ll
         }
 }

     return ret;
 }

7，部分匹配表的使用（KMP 算法）：

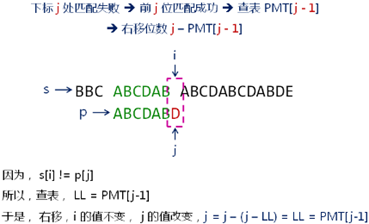
1，不匹配时，移动位置，之后直接从/字符串的/不匹配前字符/的部分匹配值下标处/开始匹配；

8，KMP 子串查找算法在 String 中的实现 ：

 /* 在字符串 s 中查找子串 p */
 int String::kmp(const char* s, const char* p)  // O(m) + O(n) ==> O(m+n)， 只有一个 for 循环
 {
     int ret = -;
     int sl = strlen(s);
     int pl = strlen(p);
 　　 int* pmt = make_pmt(p);

     if( (pmt != NULL) && ( < pl) && (pl <= sl) ) // 判断查找条件
     {
         for(int i=, j=; i<sl; i++)  // i 的值要小于目标窜长度才可以查找
         {
             while( (j > ) && (s[i] != p[j]) ) // 比对不上的时候，持续比对，
             {
                 j = pmt[j-];//移动后应该继续匹配的位置，j =j-(j -LL)=LL = PMT[j-1]
             }

             if( s[i] == p[j] )  // 比对字符成功
             {
                 j++;   // 加然后比对下一个字符
             }

             if( j == pl )  // 这个时候是查找到了，因为 j 增加到了 pl 的长度；
             {
                 ret = i +  - pl; // 匹配成功后，i 的值停在最后一个匹配成功的字符上，这样就返回匹配成功的位置

                 break;
             }
         }
 　　 }

 　　 free(pmt);

     return ret;
 }

9，小结：

1，部分匹配表是提高子串查找效率的关键；

2，部分匹配值定义为前缀和后缀最长共有元素的长度；

3，可以用递推的方法产生部分匹配表；

4，KMP 利用部分匹配值与子串移动位数的关系提高查找效率；

1，每次匹配失败的时候，子串不会简单的右移一位，而是查询部分匹配表中的值，查到后则右移一定位数，使算法效率由平方变成线性时间；