[DTOJ3996]:Lesson5!（DP+拓扑+线段树）

题目描述

　　“最短的捷径就是绕远路，绕远路就是我最短的捷径”
　　转眼就$Stage\ X$了，$Stage\ X$的比赛路线可以看做一个$n$个点$m$条边的有向无环图，每条边长度都是$1$。杰洛$\cdot$齐贝林会选择走最长的那一条路径。
　　迪亚哥$\cdot$布兰度决定摧毁一个城市以及所有关于该城市的边，由于变成恐龙后脑子有点问题，他想要让摧毁后的$Stage$最长路径最短，他想知道要摧毁哪个城市，及摧毁后最长路径的长度，如果有多个城市答案相同，则输出编号最小的那一个。

---

输入格式

　　本题包含多组数据，输入第一行一个整数$T$代表数据组数
　　每组数据第一行两个整数$n,m$表示点数，边数。
　　每组数据第$2\sim m+1$行每行两个整数$x_i,y_i$表示有一条连接$x_i,y_i$的边。

---

输出格式

　　对于每组数据，输出一行两个整数，表示删除的城市编号及删除该城市后最长路径的长度。

---

样例

样例输入：

1
6 5
1 3
1 4
3 6
3 4
4 5

样例输出：

1 2

---

数据范围与提示

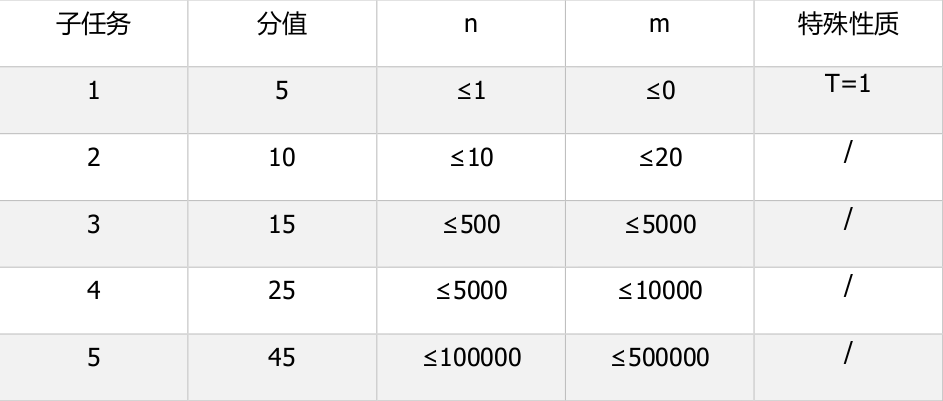
对于所有数据，满足$T\leqslant 10,1\leqslant n\leqslant 100,000,0\leqslant m\leqslant 500,000$。

---

题解

$Dijkstra$不能跑最长路！！！

解释一下。

众所周知$Dijkstra$不能跑带负边权的最短路，而跑最长路也就相当于是跑带负边权的最短路，所以它死了……

那么回来考虑这道题。

对于$DAG$，首先想到拓扑。

不妨先跑正反拓扑计算出$dis_s$和$dis_t$分别表示正反拓扑的最长路，思想类似$DP$。

那么边$i$对答案的贡献就是$dis_{s_{i_u}}+dis{t_{i_v}}+1$，删除一个点就相当与删掉了与它相连的边。

快速修改用线段树就好啦。

时间复杂度：$\Theta(m\log n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
struct rec{int nxt,to;}e[1000001];
int head[2][100001],cnt;
int n,m;
int a[100001];
int dis[2][100001],sum[100001],tr[400001],in[100001],ou[100001];
pair<int,int> ans;
queue<int> q;
void pre_work()
{
	memset(head,0,sizeof(head));
	memset(dis,0,sizeof(dis));
	memset(sum,0,sizeof(sum));
	memset(tr,0,sizeof(tr));
	memset(in,0,sizeof(in));
	memset(ou,0,sizeof(ou));
	memset(a,0,sizeof(a));
	cnt=0;ans=make_pair(1,n);
}
void add(bool id,int x,int y)
{
	e[++cnt].nxt=head[id][x];
	e[cnt].to=y;
	head[id][x]=cnt;
}
void pushup(int x){tr[x]=max(tr[L(x)],tr[R(x)]);}
void add(int x,int l,int r,int k)
{
	if(l==r)
	{
		sum[l]++;
		if(sum[l]>0)tr[x]=l;
		else{sum[l]=0;tr[x]=-1;}
		return;
	}
	int mid=(l+r)>>1;
	if(k<=mid)add(L(x),l,mid,k);
	else add(R(x),mid+1,r,k);
	pushup(x);
}
void del(int x,int l,int r,int k)
{
	if(l==r)
	{
		sum[l]--;
		if(sum[l]>0)tr[x]=l;
		else{sum[l]=0;tr[x]=-1;}
		return;
	}
	int mid=(l+r)>>1;
	if(k<=mid)del(L(x),l,mid,k);
	else del(R(x),mid+1,r,k);
	pushup(x);
}
int main()
{
	freopen("johnny.in","r",stdin);
	freopen("johnny.out","w",stdout);
	int T;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		pre_work();
		for(int i=1;i<=m;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			add(0,x,y);in[y]++;
			add(1,y,x);ou[x]++;
		}
		for(int i=1;i<=n;i++)if(!in[i]){a[++a[0]]=i;q.push(i);}
		while(q.size())
		{
			int x=q.front();q.pop();
			for(int i=head[0][x];i;i=e[i].nxt)
			{
				if(dis[0][e[i].to]<dis[0][x]+1)dis[0][e[i].to]=dis[0][x]+1;
				in[e[i].to]--;
				if(!in[e[i].to]){a[++a[0]]=e[i].to;q.push(e[i].to);}
			}
		}
		for(int i=1;i<=n;i++)if(!ou[i])q.push(i);
		while(q.size())
		{
			int x=q.front();q.pop();
			for(int i=head[1][x];i;i=e[i].nxt)
			{
				if(dis[1][e[i].to]<dis[1][x]+1)dis[1][e[i].to]=dis[1][x]+1;
				ou[e[i].to]--;
				if(!ou[e[i].to])q.push(e[i].to);
			}
		}
		for(int i=1;i<=n;i++)add(1,0,n,dis[1][i]);
		for(int x=1;x<=n;x++)
		{
			for(int i=head[1][a[x]];i;i=e[i].nxt)del(1,0,n,dis[0][e[i].to]+dis[1][a[x]]+1);
			del(1,0,n,dis[1][a[x]]);
			if(tr[1]<ans.second||(ans.second==tr[1]&&a[x]<ans.first))ans=make_pair(a[x],tr[1]);
			for(int i=head[0][a[x]];i;i=e[i].nxt)add(1,0,n,dis[0][a[x]]+dis[1][e[i].to]+1);
			add(1,0,n,dis[0][a[x]]);
		}
		printf("%d %d\n",ans.first,ans.second);
	}
	return 0;
}

---

rp++