POJ 2663 Tri Tiling 【状压DP】

Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? 
Here is a sample tiling of a 3x12 rectangle.

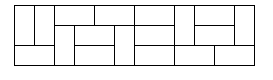
Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

题解

看了别人的博客都是递推啥的，

之前自己推了半天推不出来，智商捉鸡，就放着没做了

直到我做了POJ 2411后

再回来看这题，就是把宽度设为3而已...

#include <iostream>
#include <cstdio>       //EOF,NULL
#include <cstring>      //memset
#include <cmath>        //ceil,floor,exp,log(e),log10(10),hypot(sqrt(x^2+y^2)),cbrt(sqrt(x^2+y^2+z^2))
#include <algorithm>    //fill,reverse,next_permutation,__gcd,
#include <string>
#include <vector>
#include <queue>
#include <stack>
#include <map>
using namespace std;
#define rep(i, a, n)        for (int i = a; i < n; ++i)
#define sca(x)            scanf("%d", &x)
#define sca2(x, y)        scanf("%d%d", &x, &y)
#define sca3(x, y, z)        scanf("%d%d%d", &x, &y, &z)
#define pri(x)            printf("%d\n", x)
#define pb    push_back
#define mp    make_pair
typedef pair<int, int>        P;
typedef long long        ll;
const ll inf = ;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+;
const int maxn = ;
const int N = 1e4 + ;
int t, n, m;
int cnt, ans, ed;
ll dp[][<<];
int path[][];
int h, w;
void dfs(int l, int now, int pre)
{
    if (l > w) {
        return;
    }
    if (l == w) {
        path[cnt][] = pre;
        path[cnt++][] = now;
        return;
    }
    dfs(l + , (now << )|, (pre << )|); // 竖放，当前行为1，上一行为0
    dfs(l + , (now << )|, (pre << )); // 横放 当前行和上一行都为11
    dfs(l + , (now << ), (pre << )|);  //不放，上一行为1，当前行为0
}

int main()
{
    while (sca(h) && h != -)
    {
        w = ;
        cnt = ;
        dfs(, , );
        memset(dp, , sizeof dp);
        ed = ( << w) - ;
        dp[][ed] = ;
        for (int i = ; i < h; i++)
        {
            for (int j = ; j < cnt; j++)
            {
                dp[i + ][path[j][]] += dp[i][path[j][]];
            }
        }
        printf("%lld\n", dp[h][ed]);
    }
    return ();
}