<数据结构基础学习>（四）链表 Part 1

一.链表基础

动态数组、栈、队列底层都是依托静态数组实现的，靠resize来解决固定容量问题。

链表是真正的动态数据结构，是一种最简单的一种动态数据结构。

更深入的理解引用（或者指针）。

更深入的理解递归。

辅助成其他数据结构。

二.链表 LinkedList

数据存储在“节点”（Node）中

class Node{

E e;

　Node next;

}

最后一个节点nxet = null

优点：真正的动态，不需要处理固定容量的问题。

缺点：丧失了随机访问的能力（即给出索引直接得到索引位置的元素）

数组与链表的比较：

1.数组最好用于索引有语意的情况

最大的优点：支持快速查询

2.链表不适合用于索引有语意的情况

最大的优点：动态

三.链表的方法实现

新建类LinkedList<E>

1.为了对用户屏蔽底层实现，在LinkedList中建立内部类Node。

在内部类中设置关于Node的构造方法

public class LinkedList<E> {
    //节点设置为内部类，链表结构内可以访问Node，用户外部不可访问
    //对用户屏蔽底层实现
    private class Node{
        public E e;
        public Node next;

        public Node(E e, Node next){
            this.e = e;
            this.next = next;
        }

        public Node(E e){
            this(e, null);
        }

        public Node(){
            this(null,null);
        }

        @Override
        public String toString() {
            return e.toString();
        }
    }

2.成员变量与基本方法

链表头要存储为head

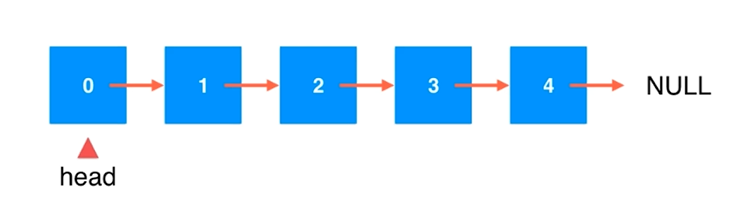
数组尾部添加元素是非常方便的（size指向最后一个元素的下一位）

在链表头添加元素是非常方便的（head跟踪链表头）

基本的成员变量为head和size

  //基本成员变量
    private Node head;
    private int size;

基本方法

    //  构造函数
    public LinkedList(){
        head = null;
        size = 0;
    }

    //获取链表中元素个数
    public int getSize(){
        return size;
    }

    //返回链表是否为空
    public boolean isEmpty(){
        return size == 0;
    

3.插入元素

1)向表头添加元素

a.设置插入元素为node

b.node的next指向head，即node.next = head

c.让head = node，即head = node

其实可以化为一句：head = new Node(e, head);

d.最后维护size，size ++

 //在链表头添加新的元素e
    public void addFirst(E e){
        Node node = new Node(e);
        node.next = head;
        head = node;
        // head = new Node(e, head);
        size ++;
    }

2)链表中间添加元素

a.对index进行判断，若index < 0 || index>size，则抛出异常index不合法。若index = 0，则直接调用addFirst()方法在表头添加元素

b.创建插入节点node

c.从head开始循环遍历寻找插入节点索引的前一个节点prev

node.next = prev.next;

prev.next = node;   顺序不能颠倒

化为一句话：prev.next=new Node(e, prev.next);

d.最后维护size，size ++

    //在链表index（0-based）位置添加新的元素
    //在链表中不是一个常用操作
    public void add(int index, E e){
        if(index < 0 || index > size){
            throw new IllegalArgumentException("Add failed. Illagal index.");
        }

        if(index == 0){
            addFirst(e);
        }else
            //找到待插入节点的前一个节点
            {
            Node prev = head;
            for(int i = 0 ; i < index - 1 ; i ++){
                prev = prev.next;
            }
            Node node = new Node(e);
            node.next = prev.next;
            prev.next = node;
            //prev.next = new Node(e, prev.next);
            size ++;
        }

    }

3)链表末尾添加元素，直接调用add()方法。

    //链表末尾添加元素e
    public void addLast(E e){
        add(size, e);
    }

4)常用技巧：为链表设立虚拟头节点

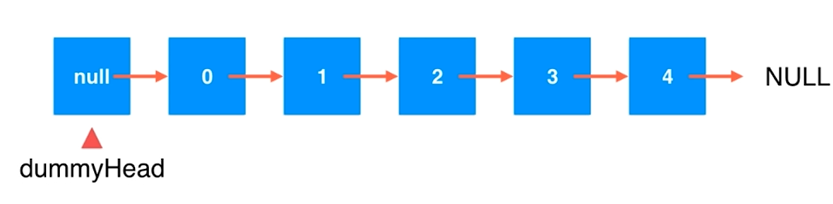
首节点元素 为dummyHead.next

需要对基本成员变量和构造函数进行修改

  //基本成员变量
    private Node dummyhead;
    private int size;

    //  构造函数
    public LinkedList(){
        dummyhead = new Node(null,null);
        size = 0;
    }

对添加方法进行修改，循环遍历次数由index-1变为index，因为加了虚拟头节点，多了一位。

　　 //在链表index（0-based）为值添加新的元素
    //在链表中不是一个常用操作
    public void add(int index, E e){
        if(index < 0 || index > size){
            throw new IllegalArgumentException("Add failed. Illagal index.");
        }
        Node prev = dummyhead;
        for(int i = 0 ; i < index  ; i ++){
           prev = prev.next;
        }
           Node node = new Node(e);
           node.next = prev.next;
           prev.next = node;
           //prev.next = new Node(e,next);
           size ++;

    }

但此时不用对index是否为0进行判断，addFirst()方法也可以优化为

   //在链表头添加新的元素e
    public void addFirst(E e){
        add(0, e);
    }

4.链表的查询操作

当找index位置前一个位置的节点，从dummyhead开始遍历

当找index位置的节点，从dummyhead.next开始遍历

获得链表index位置的元素

a.先判断index是否合法

b.令Node cur = dummyhead.next，开始遍历index次，循环体中令cur=cur.next

c.返回cur.e

//获得链表index（0-based）位置的元素
    //在链表中不是一个常用操作
    public E get(int index){
        if(index < 0 || index >= size){
            throw new IllegalArgumentException("Get failed. Illegal index");
        }

        Node cur = dummyhead.next;
        for( int i = 0 ; i < index ; i ++){
            cur = cur.next;
        }
        return cur.e;

    }

由此得到getFirst()方法和getLast()方法，getLast()方法中为get(size - 1)

　　//获得链表的第一个元素
    public E getFirst(){
        return get(0);
    }

    //获得链表最后一位元素
    public E getLast(){
        return get(size - 1);
    }

5.修改链表中index位置的方法set(int index, E e)

a.先判断index是否合法

b.令Node cur = dummyhead.next，开始遍历index次，循环体中令cur=cur.next

c.令cur.e = e

 //修改链表的第index(0-based)位置的元素为e
    //在链表中不是一个常用的操作
    public void set(int index, E e){
        if(index < 0 || index >= size){
            throw new IllegalArgumentException("Get failed. Illegal index");
        }

        Node cur = dummyhead.next;
        for( int i = 0 ; i < index ; i ++){
            cur = cur.next;
        }
        cur.e = e;
    }

6.查询链表是否存在元素e

新的遍历形式

　　//查找是否存在元素e
    public boolean contains(E e){
        Node cur = dummyhead.next;
        while(cur == null){
            if(cur.e.equals(e)){
                return true;
            }
            cur = cur.next;
        }
        return false;
    }

7.重写toString()方法

    @Override
    public String toString() {

        StringBuilder res = new StringBuilder();
//        Node cur = dummyhead.next;
//        while(cur != null){
//            res.append(cur+"->");
//            cur = cur.next;
//        }
        for(Node cur = dummyhead.next ; cur != null ; cur = cur.next){
            res.append(cur + "—>");
        }
        res.append("NULL");
        return res.toString();
    }

现在对于遍历整个链表有两种形式

1）

       Node cur = dummyhead.next;
      while(cur != null){
            res.append(cur+"->");
            cur = cur.next;
        }

2）

for(Node cur = dummyhead.next ; cur != null ; cur = cur.next){
            res.append(cur + "—>");
        }

8.链表中元素的删除

有虚拟头节点的链表

1)删除“索引”为index位置的元素delNode

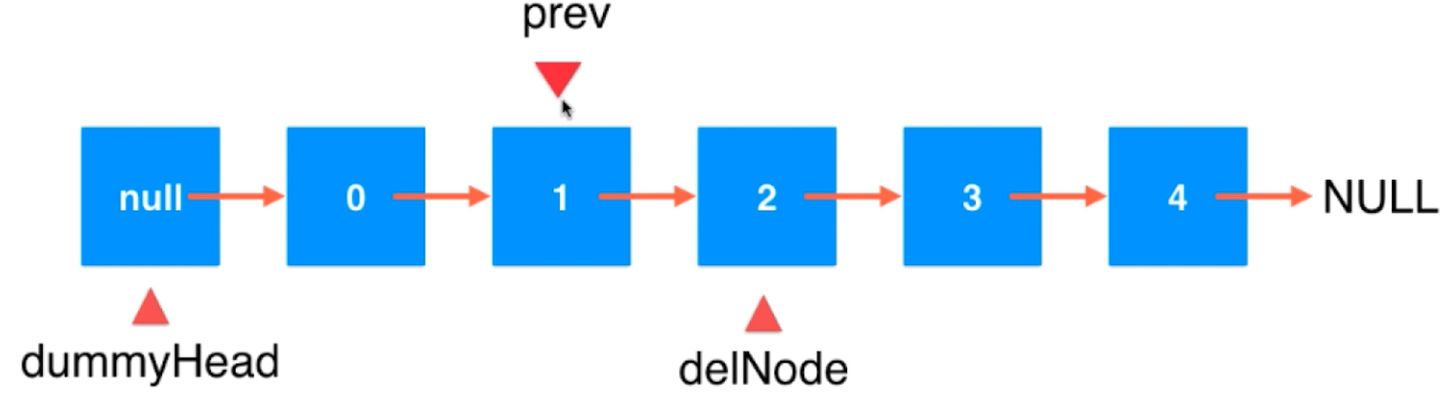
a.先判断index是否合法

b.Node prev = dummyhead；用for循环遍历查找索引为index位置的元素delNode

c. prev.next = delNode.next;

delNode.next = null;

d. 对size进行维护，size --

    //删除index(0-based)位置的元素
    public E remove(int index){
        if(index < 0 || index >= size){
            throw new IllegalArgumentException("Get failed. Illegal index");
        }
        Node prev = dummyhead;
        for( int i = 0 ; i < index  ; i ++){
            prev = prev.next;
        }
        Node retNode = prev.next;
        prev.next = retNode.next;
        retNode.next = null;
        size --;

        return retNode.e;

    }

2）删除链表第一位和最后一位的元素

    //删除第一个元素
    public E removeFirst(){
        return remove(0);
    }

    //删除最后一个元素
    public E removeLast(){
        return  remove(size-1);
    }

三.时间复杂度分析

添加操作

addLast(e)  O(n)

addFirst(e)  O(1)  与数组相反

add(index, e)   O(n/2) = O(n)

删除操作

removeLast(e)  O(n)

removeFirst(e)  O(n)

remove(index, e)  O(n/2) = O(n)

修改操作

set(index, e)  O(n)

查找操作 O(n)

get(index)   O(n)

contains(e)   O(n)

增、删、改、查均为O(n)

对链表头进行增加，删除，查询时时间复杂度为O(1)。

四.总结

1.链表是真正的动态数据结构，不需要处理固定容量的问题。

2.数组尾部添加元素是非常方便的（size指向最后一个元素的下一位）

在链表头添加元素是非常方便的（head跟踪链表头）

3.为链表设立虚拟头节点，可以让很多方法实现起来更方便

4.当找index位置前一个位置的节点，从dummyhead开始遍历

当找index位置的节点，从dummyhead.next开始遍历

5.对于链表遍历所有元素的方式有多种

6.增、删、改、查的时间复杂度均为O(n)

对链表头进行增加，删除，查询时时间复杂度为O(1)。