机器学习之正则化【L1 & L2】

前言

L1、L2在机器学习方向有两种含义：一是L1范数、L2范数的损失函数，二是L1、L2正则化

L1范数、L2范数损失函数

L1范数损失函数：

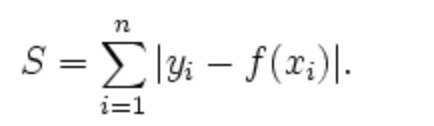
L2范数损失函数：

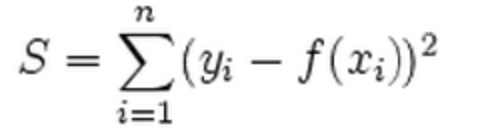
L1、L2分别对应损失函数中的绝对值损失函数和平方损失函数

区别：

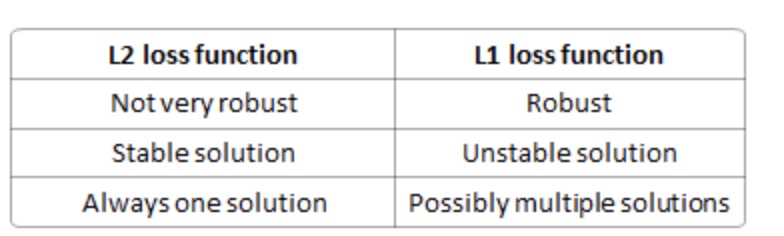
分析：

robust: 与L2相比，L1受异常点影响比较小，因此稳健

stable: 如果仅一个点，L1就是一个直线，L2是二次，对于直线来说是多解，因此不稳定，而二次函数只有一个极小值点

L1、L2正则化

为什么出现正则化？

正则化的根本原因是 输入样本的丰度不够，不能涵盖所有的情况。

解决策略 ：

• 对数据源扩充的方法：

输⼊数据源加上满⾜⼀定分布律的噪声，然后把加上噪声后的输⼊源当作“伪”新训练样本。

针对图⽚，还可以采取部分截取、⾓度旋转等数据增强⼿段，增加“新”样本。对于词表，可以增加单词的近义词，也能达到类似的效果。

• ⽹络权值的修正

神经⽹络的训练，对某些权值较为敏感。对权值稍微进⾏⼀些修改，训练的结果可能就迥然不同，所以为了保证⽹络的泛化能⼒，有必要对权值进⾏修正。具体的做法是，在⽹络的权值上加上符合⼀定分布规律的噪声，然后再重新训练⽹络，这样就增加了整个⽹络的“抗打击”能⼒，⽹络的输出结果就不会随数据源的变化⽽有很⼤变动

• 采取“早停”策略

提前停⽌训练。虽然接着训练可能会让训练误差变⼩，但让泛化误差更⼩，才是我们更⾼的⽬标

• 也可以采用集成方法，训练多个模型
• dropout

其本质就是通过改变神经⽹络的结构，⼈为添加⽹络的不确定性，从⽽锻炼神经⽹络的泛化能⼒。换句话说，通过丢弃部分节点，让各个⼦⽹络变得不同

一、L1的出现是为了解决什么问题？怎么解决的

L1就是参数的绝对值之和，它的目的就是为了产生一个关于参数w的稀疏矩阵

1、为什么会产生稀疏矩阵？

参考：https://www.zhihu.com/question/37096933

首先，我们要优化的是这个问题  。

其次，  和 

这个优化问题是等价的，即对一个特定的  总存在一个  使得这两个问题是等价的（这个是优化里的知识）。

最后，下面这个图表达的其实 

这个优化问题，把  的解限制在黄色区域内，同时使得经验损失尽可能小

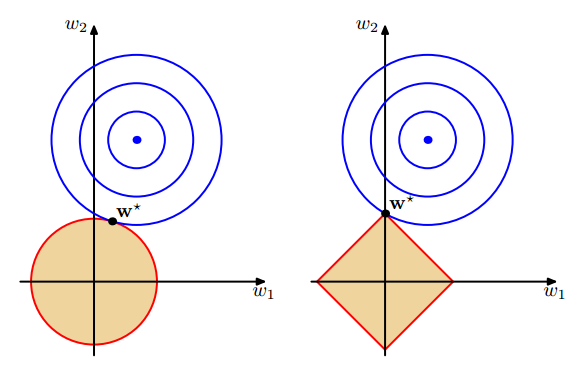
【高频面试题】为什么l1比l2更容易得到稀疏解？https://www.zhihu.com/question/37096933

从两方面解释，一是直观解释，另一种是梯度推导

【直观解释】

如上所述，无论是L1，还是L2都可以看成一种条件优化问题，L1所对应的优化区间是个菱形（右图），L2对应的是个圆形，而最优解就是 等高线与限定区间的交点，对于L1，交点是在坐标轴上，对于L2，交点是不在坐标轴上，所以L1更容易得到稀疏解。

【梯度解释】

2、产生稀疏矩阵的目的？

参考：https://blog.csdn.net/zouxy09/article/details/24971995

产生稀疏矩阵的好处可以从特征选择来解释

1）实现特征的自动选择

用于训练的数据的特征维度非常多，并且这么多的特征对于最后的结果来说并不是所有的都有用，而且特征之间还有线性关系，当考虑这些无用的特征xi时，可以获得较小的训练误差（不太理解），但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确y_i的预测。所以L1会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

二、为什么会出现L2

L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项||W||₂最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象 。

L2的好处：

1）、防止过拟合，提高泛化能力

2）、从优化或者数值计算的角度来说，L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题（不理解）

L1会趋向于产生少量的特征，而其他的特征都是0，从而产生稀疏矩阵，自动选择特征，而L2会考虑更多的特征，这些特征都会接近于0，因此不是稀疏矩阵。

疑问：

1）产生稀疏矩阵好还是不产生稀疏矩阵好，产生稀疏矩阵感觉有点降维的感觉，会选择有用的特征？

感觉L2比L1好，因为L2产生的接近于稀疏的矩阵，不是0但接近0，这样能考虑更多的特征，而对没用的特征不会一棍子打死，只是给一个很小的权重

三、Tensorflow中L1、L2的实现 

tf.nn.l2_loss(t, name=None)对t采用l2范式进行计算：output = sum(t ** 2) / 2， t是一维或者多维数组。

tf.add_n([p1, p2, p3....]) 实现列表元素相加，p1, p2, p3分别表示列表

一种显示的计算：

loss = (tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
    logits=out_layer, labels=tf_train_labels)) +
    0.01*tf.nn.l2_loss(hidden_weights) +
    0.01*tf.nn.l2_loss(hidden_biases) +
    0.01*tf.nn.l2_loss(out_weights) +
    0.01*tf.nn.l2_loss(out_biases))#考虑了weight和bias

一种隐式的计算：

vars   = tf.trainable_variables() //获取所以的变量
lossL2 = tf.add_n([ tf.nn.l2_loss(v) for v in vars ]) * 0.001 //所有的变量使用l2计算方式累加
//不考虑bias的情况
lossL2 = tf.add_n([ tf.nn.l2_loss(v) for v in vars
                    if 'bias' not in v.name ])
//把l2损失加入到loss项里
loss = (tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
    logits=out_layer, labels=tf_train_labels)) +
    0.001*lossL2)

L1不可导点如何优化：

1、坐标轴下降法

2、近似算法

https://www.cnblogs.com/ZeroTensor/p/11099332.html

参考：

[1] http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/

[2] https://blog.csdn.net/chaowang1994/article/details/80388990