CodeForces Round #515 DIv.3 F. Yet another 2D Walking

http://codeforces.com/contest/1066/problem/F

Maksim walks on a Cartesian plane. Initially, he stands at the point (0,0)(0,0) and in one move he can go to any of four adjacent points (left, right, up, down). For example, if Maksim is currently at the point (0,0)(0,0), he can go to any of the following points in one move:

• (1,0)(1,0);
• (0,1)(0,1);
• (−1,0)(−1,0);
• (0,−1)(0,−1).

There are also nn distinct key points at this plane. The ii-th point is pi=(xi,yi)pi=(xi,yi). It is guaranteed that 0≤xi0≤xi and 0≤yi0≤yi and there is no key point (0,0)(0,0).

Let the first level points be such points that max(xi,yi)=1max(xi,yi)=1, the second level points be such points that max(xi,yi)=2max(xi,yi)=2 and so on. Maksim wants to visit all the key points. But he shouldn't visit points of level i+1i+1 if he does not visit all the points of level ii. He starts visiting the points from the minimum level of point from the given set.

The distance between two points (x1,y1)(x1,y1) and (x2,y2)(x2,y2) is |x1−x2|+|y1−y2||x1−x2|+|y1−y2| where |v||v| is the absolute value of vv.

Maksim wants to visit all the key points in such a way that the total distance he walks will be minimum possible. Your task is to find this distance.

If you are Python programmer, consider using PyPy instead of Python when you submit your code.

Input

The first line of the input contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of key points.

Each of the next nn lines contains two integers xixi, yiyi (0≤xi,yi≤1090≤xi,yi≤109) — xx-coordinate of the key point pipi and yy-coordinate of the key point pipi. It is guaranteed that all the points are distinct and the point (0,0)(0,0) is not in this set.

Output

Print one integer — the minimum possible total distance Maksim has to travel if he needs to visit all key points in a way described above.

Examples

input

Copy

8
2 2
1 4
2 3
3 1
3 4
1 1
4 3
1 2

output

Copy

15

input

Copy

5
2 1
1 0
2 0
3 2
0 3

output

Copy

9

Note

The picture corresponding to the first example: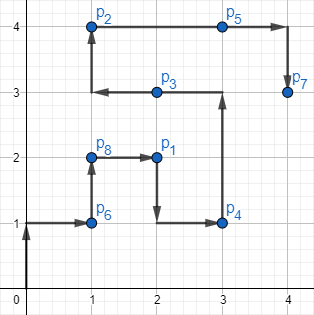

There is one of the possible answers of length 1515.

The picture corresponding to the second example: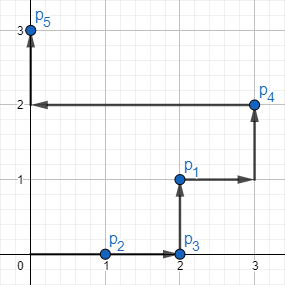

There is one of the possible answers of length 99.

代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 200010;
int N, len = 1, t = 1;
ll dp[maxn][5];

struct Node{
    int x;
    int y;
}node[maxn], st;
vector<Node> v[maxn];

bool cmp(const Node& a, const Node& b) {
    if(max(a.x, a.y) == max(b.x, b.y))
        return a.x == b.x ? a.y < b.y : a.x > b.x;
	return max(a.x, a.y) < max(b.x, b.y);
}

ll solve(ll x) {
    return x >= 0 ? x : -x;
}

ll Solve() {
    dp[1][0] = dp[1][1] = 0;
	for(int i = 1; i <= len; i ++) {
		ll dis00 = solve(v[i - 1][0].x - v[i][0].x) + solve(v[i - 1][0].y - v[i][0].y);
		ll dis01 = solve(v[i - 1][0].x - v[i][1].x) + solve(v[i - 1][0].y - v[i][1].y);
		ll dis10 = solve(v[i - 1][1].x - v[i][0].x) + solve(v[i - 1][1].y - v[i][0].y);
		ll dis11 = solve(v[i - 1][1].x - v[i][1].x) + solve(v[i - 1][1].y - v[i][1].y);
		dp[i][0] = min(dp[i - 1][0] + dis10, dp[i - 1][1] + dis00);
		dp[i][1] = min(dp[i - 1][1] + dis01, dp[i - 1][0] + dis11);
	}
	return min(dp[len][0], dp[len][1]);
}

int main() {
    scanf("%d", &N);
    for(int i = 1; i <= N; i ++)
        scanf("%d%d", &node[i].x, &node[i].y);

    st.x = 0, st.y = 0;
    v[0].push_back(st);
    sort(node + 1, node + 1 + N, cmp);

    ll ans = 0;
    while(t <= N) {
        v[len].push_back(node[t]);

        int now = t;
        while(t < N && max(node[t + 1].x, node[t + 1].y) == max(node[now].x, node[now].y))
            t ++;
        v[len ++].push_back(node[t]);

        ans += (solve((ll)(node[t].x - node[now].x)) + solve((ll)(node[t].y - node[now].y)));
        t ++;
    }
    len --;
    ans += Solve();
    printf("%lld\n", ans);
    //printf("%d\n", len);
    return 0;
}