「BZOJ2127」happiness（最小割）

题目描述

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。

作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

输入输出格式

输入格式：

第一行两个正整数n，m。

接下来是六个矩阵

第一个矩阵为n行m列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。

第二个矩阵为n行m列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。

第三个矩阵为n-1行m列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。

第四个矩阵为n-1行m列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。

第五个矩阵为n行m-1列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。

第六个矩阵为n行m-1列

此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

输出格式：

输出一个整数，表示喜悦值总和的最大值

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

【样例说明】

两人都选理，则获得100+110+1000的喜悦值。

对于100%以内的数据，n,m<=100 所有喜悦值均为小于等于5000的非负整数

题解

　额，这题最重要的是一个模型转换的思想。因为最小割可以代表选择或不选择，那么我们就让每一个最小割的状态分别代表题目所示的每一个状态

　　先考虑建图，假设$A$和$B$是有关联的两点，那么建如下的图

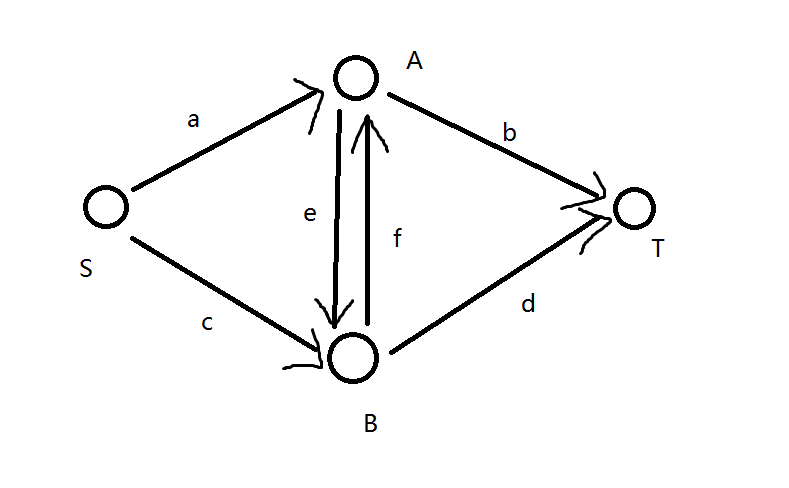
　　其中$S$表示源点，代表文科，$T$表示汇点，代表理科，$A,B$是互相关联的两点。这张图的意思是，如果某个点与$S$相连，代表它选择文科，如果与$T$相连，代表它选择理科

　　那么我们考虑一下，要怎么样才能使全文，全理，一文一理三种情况都能出现呢？

　　我们考虑图中边的流量，a=A文+AB文/2，c=B文+AB文/2，b=A理+AB理/2，d=B理+AB理/2，e=f=AB文/2+AB理/2

　　因为最小割的割可以代表选择，所以我们可以通过枚举割来枚举选择。那么上图中是不是每一个割都代表了一种选择呢？

　　我们设sum=A文+B文+A理+B理+AB文+AB理

　　当两人都选文时，我们割去b，d，那么割的大小为A理+B理+AB理，用sum减去割剩下的就是全选文的高兴值

　　如果两人都选理，那么我们割去a，c，和上面一个一样，就不多说

　　如果两人一文一理怎么办呢？我们假设A文B理，割去a，f，d，那么sum减去割的大小就是A选文和B选理的高兴值

　　综上所述，不难发现上图的每一个割都代表了一种选择的状态。那么我们要令高兴值最大，那么割必须最小，只要求出一个最小割就行了

　　代码参考（抄）了hzwer的

 // luogu-judger-enable-o2

 //minamoto

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<queue>

 #define inf 0x3f3f3f3f

 using namespace std;

 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)

 char buf[<<],*p1=buf,*p2=buf;

 inline int read(){

     #define num ch-'0'

     char ch;bool flag=;int res;

     while(!isdigit(ch=getc()))

     (ch=='-')&&(flag=true);

     for(res=num;isdigit(ch=getc());res=res*+num);

     (flag)&&(res=-res);

     #undef num

     return res;

 }

 const int N=,M=;

 int head[N],Next[M],ver[M],edge[M],tot=;

 int dep[N],cur[N],n,m,s,t,mxflow;

 int a[][],b[][],id[][],ans;

 queue<int> q;

 inline void add_edge(int u,int v,int e){

     ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;

 }

 inline void ins(int u,int v,int e){

     add_edge(u,v,e),add_edge(v,u,e);

 }

 inline void insert(int u,int v,int e){

     add_edge(u,v,e),add_edge(v,u,);

 }

 bool bfs(){

     memset(dep,-,sizeof(dep));

     while(!q.empty()) q.pop();

     for(int i=s;i<=t;++i) cur[i]=head[i];

     q.push(s),dep[s]=;

     while(!q.empty()){

         int u=q.front();q.pop();

         for(int i=head[u];i;i=Next[i]){

             int v=ver[i];

             if(dep[v]<&&edge[i]){

                 dep[v]=dep[u]+,q.push(v);

                 if(v==t) return true;

             }

         }

     }

     return false;

 }

 int dfs(int u,int limit){

     if(u==t||!limit) return limit;

     int flow=,f;

     for(int i=cur[u];i;i=Next[i]){

         int v=ver[i];cur[u]=i;

         if(dep[v]==dep[u]+&&(f=dfs(v,min(limit,edge[i])))){

             flow+=f,limit-=f;

             edge[i]-=f,edge[i^]+=f;

             if(!limit) break;

         }

     }

     if(!flow) dep[u]=-;

     return flow;

 }

 void dinic(){

     while(bfs()) mxflow+=dfs(s,inf);

 }

 void build(){

     int x;s=,t=n*m+;

     for(int i=;i<n;++i)

     for(int j=;j<=m;++j){

         x=read(),ans+=x;

         a[i][j]+=x,a[i+][j]+=x;

         ins(id[i][j],id[i+][j],x);

     }

     for(int i=;i<n;++i)

     for(int j=;j<=m;++j){

         x=read(),ans+=x;

         b[i][j]+=x,b[i+][j]+=x;

         ins(id[i][j],id[i+][j],x);

     }

     for(int i=;i<=n;++i)

     for(int j=;j<m;++j){

         x=read(),ans+=x;

         a[i][j]+=x,a[i][j+]+=x;

         ins(id[i][j],id[i][j+],x);

     }

     for(int i=;i<=n;++i)

     for(int j=;j<m;++j){

         x=read(),ans+=x;

         b[i][j]+=x,b[i][j+]+=x;

         ins(id[i][j],id[i][j+],x);

     }

     for(int i=;i<=n;++i)

     for(int j=;j<=m;++j){

         insert(s,id[i][j],a[i][j]);

         insert(id[i][j],t,b[i][j]);

     }

 }

 int main(){

     //freopen("testdata.in","r",stdin);

     n=read(),m=read();

     for(int i=;i<=n;++i)

     for(int j=;j<=m;++j)

     a[i][j]=read(),ans+=a[i][j],a[i][j]<<=;

     for(int i=;i<=n;++i)

     for(int j=;j<=m;++j)

     b[i][j]=read(),ans+=b[i][j],b[i][j]<<=;

     for(int i=;i<=n;++i)

     for(int j=;j<=m;++j)

     id[i][j]=(i-)*m+j;

     build(),dinic();

     printf("%d\n",ans-(mxflow>>));

     return ;

 }