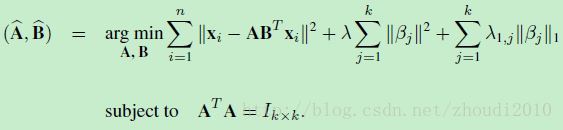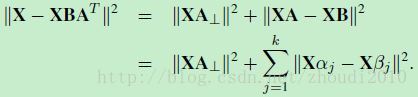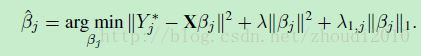Sparse PCA 稀疏主成分分析
Sparse PCA 稀疏主成分分析
SPCA原始文献:H. Zou (2006) Sparse principal component analysis
PCA 可以参考: The Elements of Statistical Learning 第十四章
主成分分析的基本思想以及R的应用可以参考:稀疏主成分分析与R应用
关于统计学习中的稀疏算法可以参考:Statistical learning with sparsity: the lasso and generalizations
一份很好的文档:http://www.cs.utexas.edu/~rashish/sparse_pca.pdf
首先直接来看算法:
- 令A初始化为V[,1:k],即为前k个principal components的loading vectors.
- 对于给定的A=[α1,…,αk]A=[α1,…,αk] , 优化elastic net:
βj=argmaxβ(αi−β)TXTX(αi−β)+λ∥β∥2+λ1,j∥β∥1βj=argmaxβ(αi−β)TXTX(αi−β)+λ‖β‖2+λ1,j‖β‖1 - 对于给定的B=[β1,…,βk]B=[β1,…,βk], 计算XTXBXTXB的SVD,更新A=UVTA=UVT.
- 重复2-3步,直到收敛.
- Normalization之后得到ViVi
接下来对该算法进行必要的解释:
想要得到稀疏的结果,核心思想是在优化参数时加入 L1L1 penalty. 另外,如果我们将PCA问题转化为regression问题,那么就达到了求解稀疏主成分的目的了。
H. Zou (2006)的Theorem 1就提出了PCA和Regression的联系。即:如果我们已经知道由SVD得到的principal components, 那么ridge estimates就是ViVi.
βridge=argmaxβ∥Zi−Xβ∥2+λ∥β∥2βridge=argmaxβ‖Zi−Xβ‖2+λ‖β‖2
如果在上式中加入L1L1 penalty: λ1∥β∥1λ1‖β‖1,那么就可以得到了sparse PCs. 但是这是一个仍然依赖PCA的结果,我们想要得到一个self-contained的方法。
所以新的优化问题是这样的形式:
第二项和第三项是elastic net,或者理解为ridge+lasso. 第一项则和之前的形式有些不同。如果我们令A=BA=B,那么第一项就变成了∥xi−AATxi∥2‖xi−AATxi‖2, 这个形式就是PCA的形式(注释1).
这一步我们遇到的问题是:
1. AA 和 BB 我们都不知道,如果同时优化,能量方程并不是凸优化问题,但固定其中一个变量,则为凸优化问题。
2. ∥xi−ABTxi∥2‖xi−ABTxi‖2 形式不方便elastic net优化
解决思路是:
1. 将问题转化为:如果AA已知,求BB;然后根据求得的BB,求AA,如此迭代。
2. 将∥xi−ABTxi∥2‖xi−ABTxi‖2 形式转化为∥Y−XTβ∥2‖Y−XTβ‖2 形式。
先说问题2的解决方法(注释2):
令Y∗=XαjY∗=Xαj
就得到了最终需要的形式:
再说问题1的算法,也就是文章最开始提到的算法中的2,3步(注释3):
如此这般,SPCA就ok了!
不过,还有几个小问题:
注释1处 为什么A=BA=B就退化成了PCA?
具体可以参考The Elements of Statistical Learning 14.5
我们为了最小化reconstruction error:
∥xi−μ−Vqλi∥2‖xi−μ−Vqλi‖2
得到 λ^i=V⊤q(xi−x¯)λ^i=Vq⊤(xi−x¯)
将其带入error,可以得到orthogonal matrix VqVq使其最小化:
∥(xi−x¯)−VqV⊤q(xi−x¯)∥2‖(xi−x¯)−VqVq⊤(xi−x¯)‖2
VqV⊤qVqVq⊤就是projection matrix.
所以A=BA=B,AA就相当于VV.
注释2处 这个转化怎么得到的?
∥X−XBA⊤∥2‖X−XBA⊤‖2 = ∥XA⊥∥2‖XA⊥‖2 + ∥XA−XB∥2‖XA−XB‖2
注意到AA为orthonomal,A⊥A⊥也是orthonomal matrix并且使得[A;A⊥][A;A⊥]是p×pp×p orthonomal matrix.
所以将 ∥X−XBA⊤∥2‖X−XBA⊤‖2 投影到AA 和A⊥A⊥可以得到 :
∥X−XBA⊤∥2‖X−XBA⊤‖2
= ∥(X−XBA⊤)A⊥∥2‖(X−XBA⊤)A⊥‖2 + ∥(X−XBA⊤)A∥2‖(X−XBA⊤)A‖2
= ∥XA⊥∥2‖XA⊥‖2 +∥XA−XB∥2‖XA−XB‖2
注释3处 A given B 怎么证明?
需要用到Procrustes Rotation的结论:
(A.7)是squared Frobenius matrix norm, 所以 ∥X∥2=trace(X⊤X)‖X‖2=trace(X⊤X).
Procrustes (普洛克路斯忒斯)是希腊神话中的一名强盗。他是海神波塞冬的儿子,在从雅典到埃莱夫西纳的路上开设黑店,拦截行人。店内设有一张铁床,旅客投宿时,将身高者截断,身矮者则强行拉长,使与床的长短相等。而由于普洛克路斯忒斯秘密地拥有两张长度不同的床,所以无人能因身高恰好与床相等而幸免。后来英雄忒修斯前往雅典时,路过此地,将其杀死。(From Wiki)
Sparse PCA 稀疏主成分分析的更多相关文章
- sparse-PCA(稀疏主成分分析)是什么?
不多说,直接上干货! 复杂降维技术有spare-PCA和sparse coding. 最近在科研需要,感谢下面的博主. Sparse PCA 稀疏主成分分析
- Deflation Methods for Sparse PCA
目录 背景 总括 Hotelling's deflation 公式 特点 Projection deflation 公式 特点 Schur complement deflation Orthogona ...
- Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]
目录 概括 Sparse PCA Formulation 非常普遍的问题 Optimality Conditions Eigenvalue Bounds 算法 代码 概括 这篇论文,不像以往的那些论文 ...
- SQL Server ->> Sparse File(稀疏文件)
Sparse File(稀疏文件)不是SQL Server的特性.它属于Windows的NTFS文件系统的一个特性.如果某个大文件中的数据包含着大量“0数据”(这个应该从二进制上看),这样的文件就可以 ...
- Sparse PCA: reproduction of the synthetic example
The paper: Hui Zou, Trevor Hastie, and Robert Tibshirani, Sparse Principal Component Analysis, Journ ...
- [综] Sparse Representation 稀疏表示 压缩感知
稀疏表示 分为 2个过程:1. 获得字典(训练优化字典:直接给出字典),其中字典学习又分为2个步骤:Sparse Coding和Dictionary Update:2. 用得到超完备字典后,对测试数据 ...
- sparse coding稀疏表达入门
最近在看sparse and redundant representations这本书,进度比较慢,不过力争看过的都懂,不把时间浪费掉.才看完了不到3页吧,书上基本给出了稀疏表达的概念以及传统的求法. ...
- A direct formulation for sparse PCA using semidefinite programming
目录 背景 Sparse eigenvectors(单个向量的稀疏化) 初始问题(low-rank的思想?) 等价问题 最小化\(\lambda\) 得到下列问题(易推) 再来一个等价问题 条件放松( ...
- PCA (主成分分析)详解 (写给初学者) 结合matlab(转载)
一.简介 PCA(Principal Components Analysis)即主成分分析,是图像处理中经常用到的降维方法,大家知道,我们在处理有关数字图像处理方面的问题时,比如经常用的图像的查询问题 ...
随机推荐
- 20175313 张黎仙《获奖感想与Java阶段性学习总结》
一.获奖感想 很荣幸能够成为为数不多的小黄衫获得者之一,这是对我近一学期以来学习成果的肯定,也激励着我更加努力学习. 首先我要感谢的人就是娄嘉鹏老师.我曾在师生关系中提到,我认为的好老师的特点之一是: ...
- 咏南中间件新增MORMOT插件功能
咏南中间件新增MORMOT插件功能 咏南中间件支持DATASNAP和MORMOT两种通讯框架. 原来已经支持DATASNAP插件,现在又增加了MORMOT插件,已经支持DATASNAP和MORMOT两 ...
- leetcode 108. Convert Sorted Array to Binary Search Tree 、109. Convert Sorted List to Binary Search Tree
108. Convert Sorted Array to Binary Search Tree 这个题使用二分查找,主要要注意边界条件. 如果left > right,就返回NULL.每次更新的 ...
- OGG-01332 ogg高版本向低版本传输
Neo君遇到的ogg版本问题,在ggserr.log中的错误信息如下: 2018-10-12 09:55:10 ERROR OGG-01332 Oracle GoldenGate Delivery, ...
- HTML5 地理位置定位API(4)
地理定位(geolocation)是最令人兴奋,而且得到了广泛支持的一个新API.通过这套API, JavaScript代码能够访问到用户的 当前位置信息.当然,访问之前必须得到用户的明确许可,即同意 ...
- CentOS 端口和防火墙操作
Centos 7 端口和防火墙命令: 查看已经开放的端口:firewall-cmd --list-ports 开启端口:firewall-cmd --zone=public --add-port=80 ...
- 偶尔在网上看到的,相对比较好的c#端订单号生成规则
偶尔在网上看到的,相对比较好的c#端订单号生成规则 public class BillNumberBuilder{ private static object locker = new obj ...
- Cas(02)——部署Cas Server
部署Cas Server Cas应用都需要有一个Cas Server.Cas Server是基于Java Servlet实现的,其要求部署在Servlet2.4以上版本的Web容器中.在此笔者将其部署 ...
- socket 异步接收连接和接收数据
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- Flutter FutureBuilder异步请求列表示例
Flutter的FutureBuilder列表示例 import 'package:flutter/material.dart'; import '../service/service_method. ...