区间统计——ST算法

一、引入

先举一个小栗子。

一数组有 $n$ 个元素，有 $m$ 次询问（$n, m <= 10^5$）。对于每次询问给出 $l, r$，求出 $[l, r]$的区间和。

有的同学说，这很简单啊！直接前缀和不就行了吗？确实如此，示例代码如下：

int n, m; cin >> n >> m;

vector< int > sum( n + 10 );

fill( sum.begin(), sum.end(), 0 );

for ( int i = 1, x; i <= n; ++i ) {

	cin >> x;

	sum[ i ] = sum[ i - 1 ] + x;

}

while ( m-- ) {

	int l, r; cin >> l >> r;

	l = min( l, r ); r = max( l, r );

	cout << sum[ r ] - sum[ l - 1 ] << endl;

}

但是，我们稍稍改变一下题目，将求区间和改为求区间最大值，前缀和就行不通了。我们应该如何在 $O(nlogn)$ 的时间复杂度下求得结果呢？

二、ST 算法介绍

上面的问题也被称为区间最值查询。（$RMQ$, $Range $ $Maximum/Minimum$ $Query$）在静态的区间最值查询问题中，我们可以使用 $ST$ 算法解决。

首先我们假定需要求解的数组为 $A=\{ 10, 20, 30, 40, 50, 60 \}$，且为了方便，数组下标从 $ 1 $ 开始。

由于问题可离线，我们可以先预处理，再输出答案。

基于倍增思想，我们可以对于每一个元素构造一个倍增数组，其内容为$A$ 中 $[i, i+2^k-1]$的最大值（$i\in( [1,n]\cap\N), i+2^k-1\leq n, k\in \N$），如下图所示：

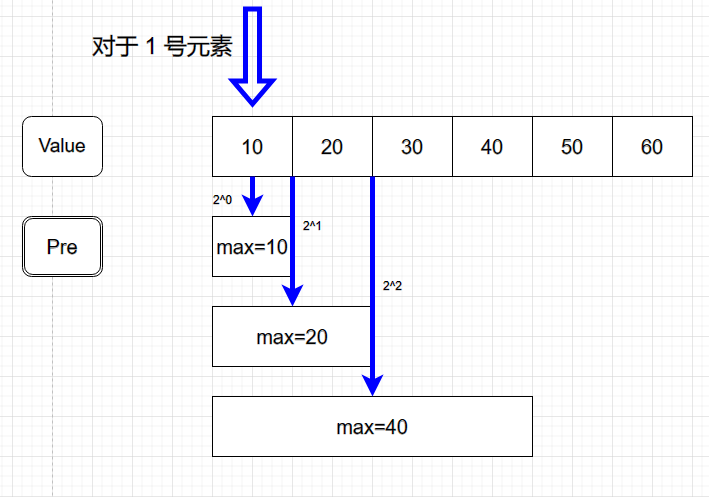
以此类推，我们可以对于每个元素构造这么一个数组，即 $Pre$ 数组为一个二维数组，可定义为：

int pre[ maxn ][ maxlog ]; // maxlog 为上文中 k 的最大值，一般取 25 左右

那么，我们该如何快速求解出 $pre[i][j]$ 呢？

三、 pre[i][j] 的求法

我们可以将 $ST$ 算法看作一个 DP。

首先，$pre[i][j]$ 本身就可以视作一个状态矩阵，存储着对应区间的最值。

接着，其边界条件是 $pre[i][0]$，即元素本身。这很容易理解，因为 $[i,i]$ 的最值本身就是 $i$ 嘛。

其次，由于预处理是离线过程，所以对于新的区间最值求解，不会对已求出区间的最值产生影响，故满足 DP 的无后效性原则。

最后，我们来整理状态转移方程。

对于区间 $[i, j]$，显然可以将其二分为 $[i, \frac{i+j}{2}]$ 和 $(\frac{i+j}{2},j)$。若知道这两个区间的最值 $p$ 和 $q$，显然地，整个$[i,j]$区间的最值必然等于$max(p,q)$或$min(p,q)$。这样问题就转化为求子区间的最值。以此类推直至边界。我们可以结合下图进行理解。

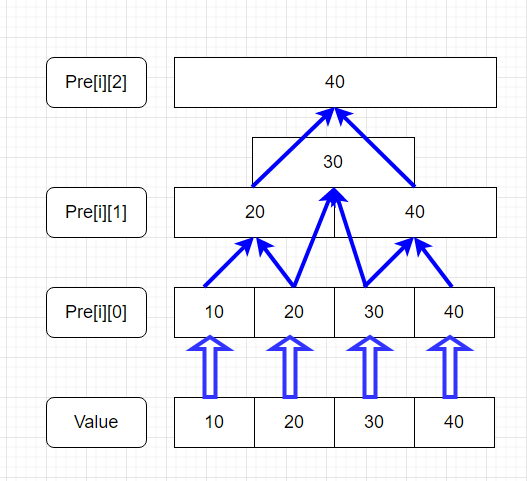
于是我们可以轻松写出代码：

int n, m; cin >> n >> m;

for ( int i = 1; i <= n; ++i ) cin >> pre[ i ][ 0 ];

for ( int j = 1; j <= maxlog; ++j )

	for ( int i = 1; i + ( 1 << j ) - 1 <= n; ++i )

		pre[ i ][ j ] = max(

			pre[ i ][ j - 1 ],	// [i, i+2^(j-1)-1] 即前半段区间

			pre[ i + ( 1 << ( j - 1 ) ) ][ j - 1 ]	// [i+2^(j-1), i+2^j-1] 即后半段区间

		); // 因为 2^j = 2 * 2^(j-1)，所以可以这么写

四、How to query?

预处理完毕，该如何实现高效查询呢？

要求的区间为 $[l, r]$，区间长度即为 $r-l+1$。得知了区间长度，我们就可以在 $Pre$ 中进行查找。由于区间长度不一定为 $ 2^k, k\in N $，我们仅取一个区间返回结果不一定准确（因为 $Pre$ 中预处理的区间长度均为 $ 2^k $）所以我们需要找到一个长度，使得其为 $ 2^k $ 且尽量长但不超过 $[l,r]$ 的长度。显然地，这个长度为 $floor(\log_{2}{(r-l+1)})$。这个长度可以直接用于 $Pre$ 且尽量大。所以所取区间为 $[l, l+2^{log_{2}{(r-l+1)}}-1]$，在 $Pre$ 数组中即为 $ pre[l][log(r-l+1)]$。对于 $\complement_{[l, l+2^{log_{2}{(r-l+1)}}-1]}{[l,r]}$，由于 $RMQ$ 问题的可重复贡献性，我们可以找两段重叠的区间取最值。所以可以从 $r$ 开始向左找长度同样为 $floor(\log_{2}{(r-l+1)})$ 的区间，使这个区间右端点为 $r$。于是第二个区间为 $ [r-2^{log_{2}{(r-l+1)}}+1,r] $，对应 $Pre$ 中即为 $pre[r-(1<<log(r-l+1))+1][log(r-l+1)]$ 。不难发现这两个区间的并集必为 $[l,r]$。即两个区间最值的 $max/min$ 一定是整个区间的最值。通过图片进行解释：

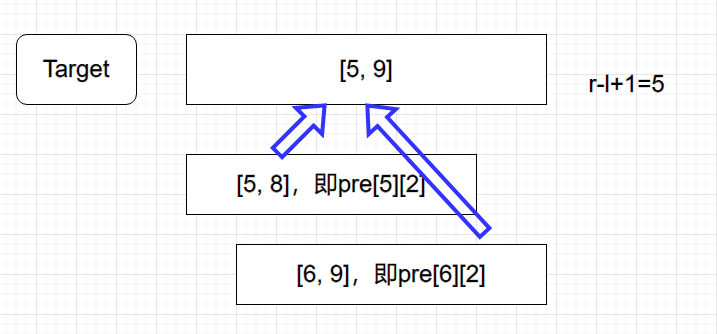
于是我们可得出 $query$ 函数的代码：

inline int query( int l, int r ) {

	int k = log( r - l + 1 );	// 简化代码

	return max(

		pre[ l ][ k ],

		pre[ r - ( 1 << k ) + 1 ][ k ]

	);

}

下面是 $ST$ 算法的模板。用于解决洛谷 P3865：

#include <bits/stdc++.h>

using namespace std;

#define k lg2[r - l + 1]

typedef long long ll;

template<typename T>

inline void read(T &x) {

    T f = 1; x = T(0); char ch = getchar();

    while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }

    while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }

    x *= f;

}

namespace SparseTable {

    const int MAXN = 2e6 + 10, MAXLOG = 25;

    int n, m, f[MAXN][MAXLOG], lg2[MAXN];

    void init(void) {

        // Read components

        read(n); read(m);

        for (int i = 1; i <= n; i++)

            read(f[i][0]);

        // Sparse Table

        for (int j = 1; j <= MAXLOG; j++)

            for (int i = 1; i + (1 << j) - 1 <= n; i++)

                f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1) )][ j - 1 ]);

        // Log2

        lg2[1] = 0; lg2[2] = 1;

        for (int i = 3; i < MAXN; i++)

            lg2[i] = lg2[i / 2] + 1;

    }

    inline int query(const int l, const int r) {

        return max(f[l][k], f[r - (1 << k) + 1][k]);

    }

}

int main(void) {

    int l, r;

    SparseTable::init();

    while ( (SparseTable::m) --) {

        read(l); read(r);

        printf("%d\n", SparseTable::query(min(l, r), max(l, r)));

    }

    return 0;

}

六、优点与局限性

$ST$ 算法有一些其他算法所不具备的优点，比如：

代码量小
常数小，时间复杂度较低

$ST$ 算法的局限性很大，只能解决静态区间可重复贡献问题，局限性如下：

可扩展性较弱
无法处理在线修改操作

第二点实际上是 $ST$ 表实际应用中最大的障碍。那么，如何解决在线修改查询问题呢？需要的两大杀器分别是树状数组和线段树（包括 zkw 线段树），这两种数据结构将在接下来的几篇文章中介绍。

七、参考资料：