leecode62不同路径(动态规划)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

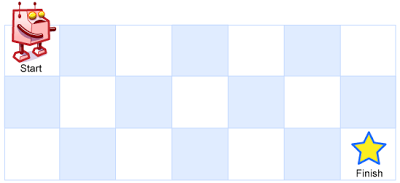
示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28
示例 4：
输入：m = 3, n = 3
输出：6

思路1：此题可以看作明显的动态规划问题，矩阵中每个点记录该点存在多少条路径，最边缘的路径肯定是1，相当与将从起点到现在走到的点打成一个小包，下次想用的时候就不需要再走一遍直接使用包中的内容即可。

代码如下所示：

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i=0;i<m;i++){
            dp[i][0] = 1;
        }
        for(int i=0;i<n;i++){
            dp[0][i] = 1;
        }
        for(int i=1 ;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

思路2：排列组合解法，其中机器人需要右移m-1次，需要向下移动n-1次那么总共需要移动m+n-2次，即公式可以写为C（m-1，m+n-2）=（m+n-2）！/（m-1）！(n-1)!