AOE网与关键路径

声明：图片及内容基于https://www.bilibili.com/video/BV1BZ4y1T7Yx?from=articleDetail

原理

AOE网

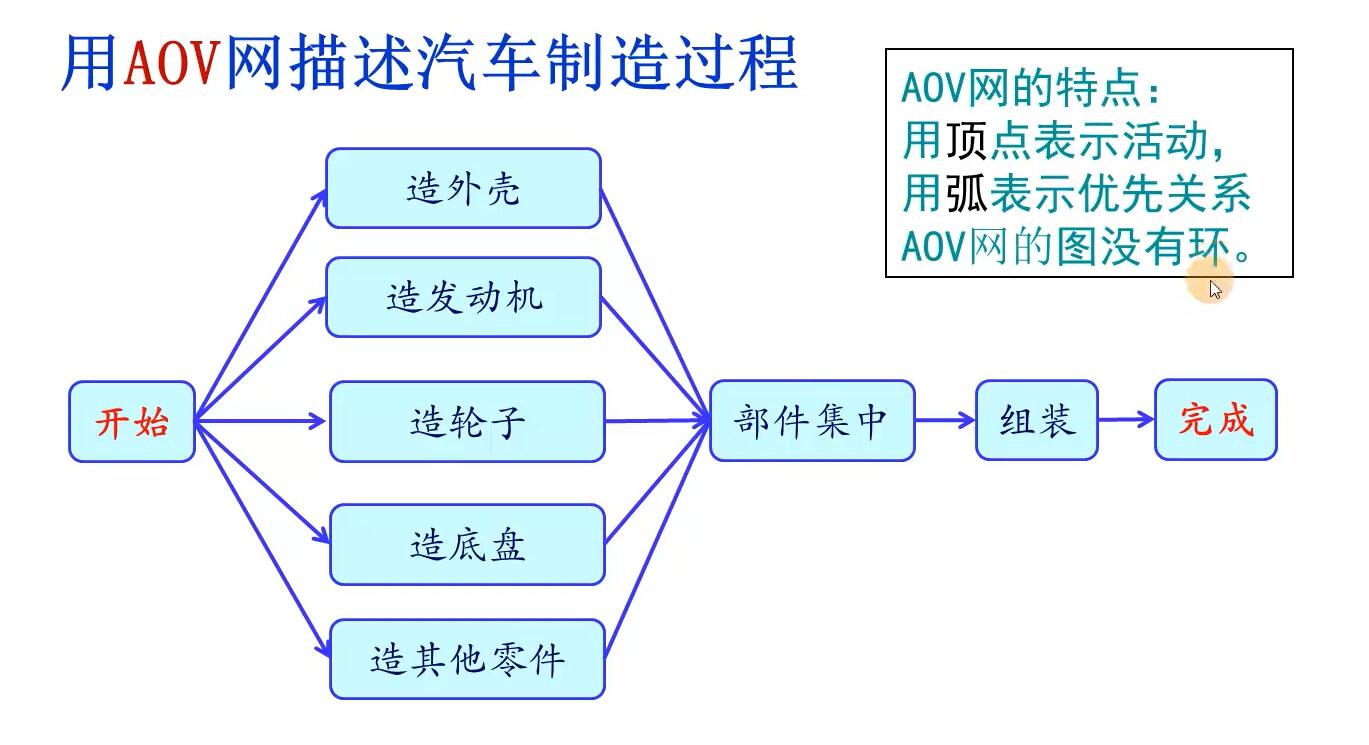
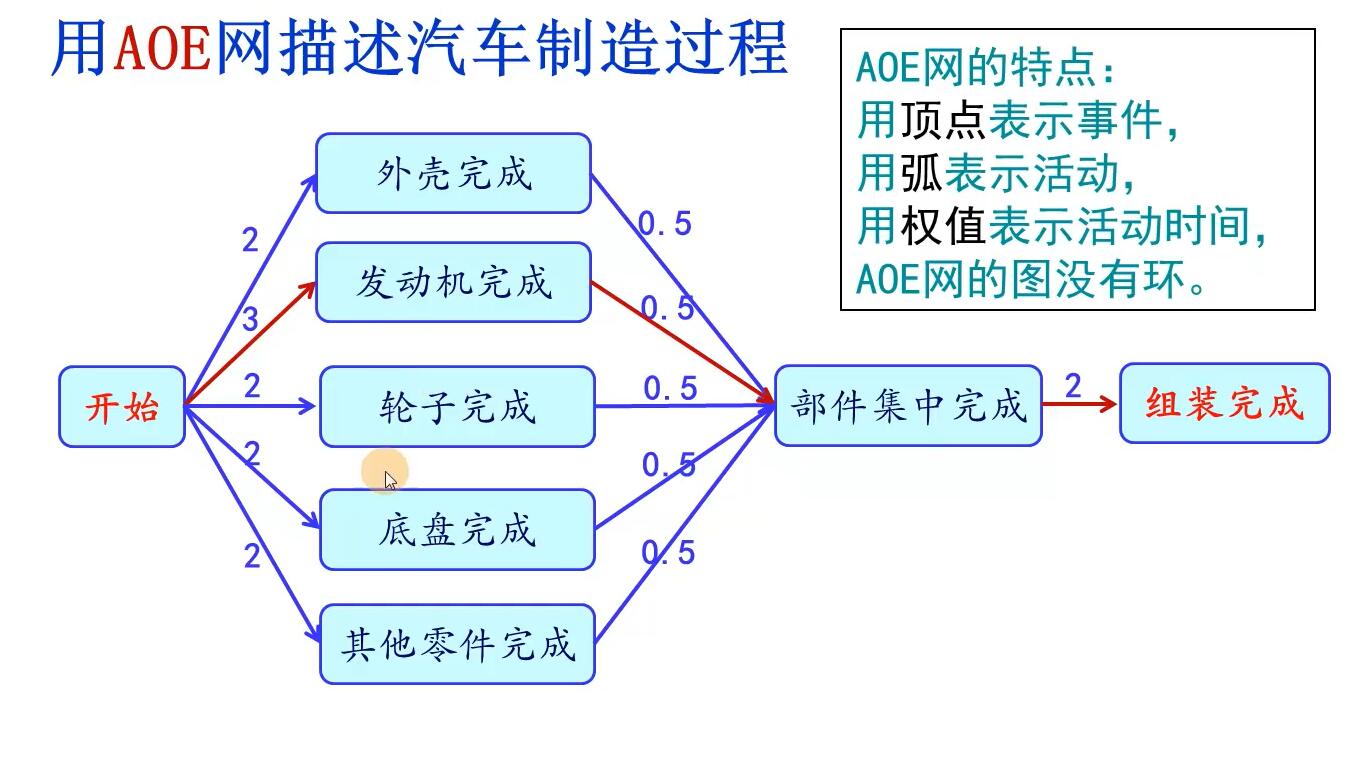
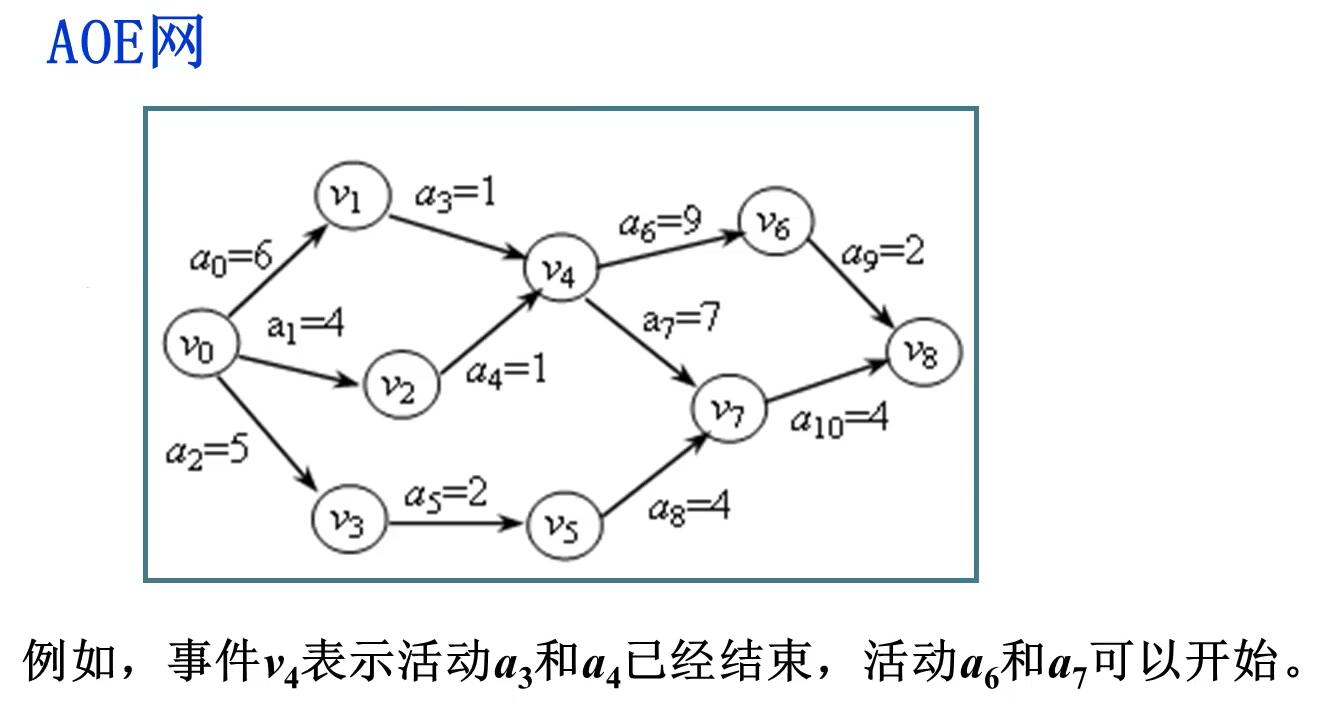
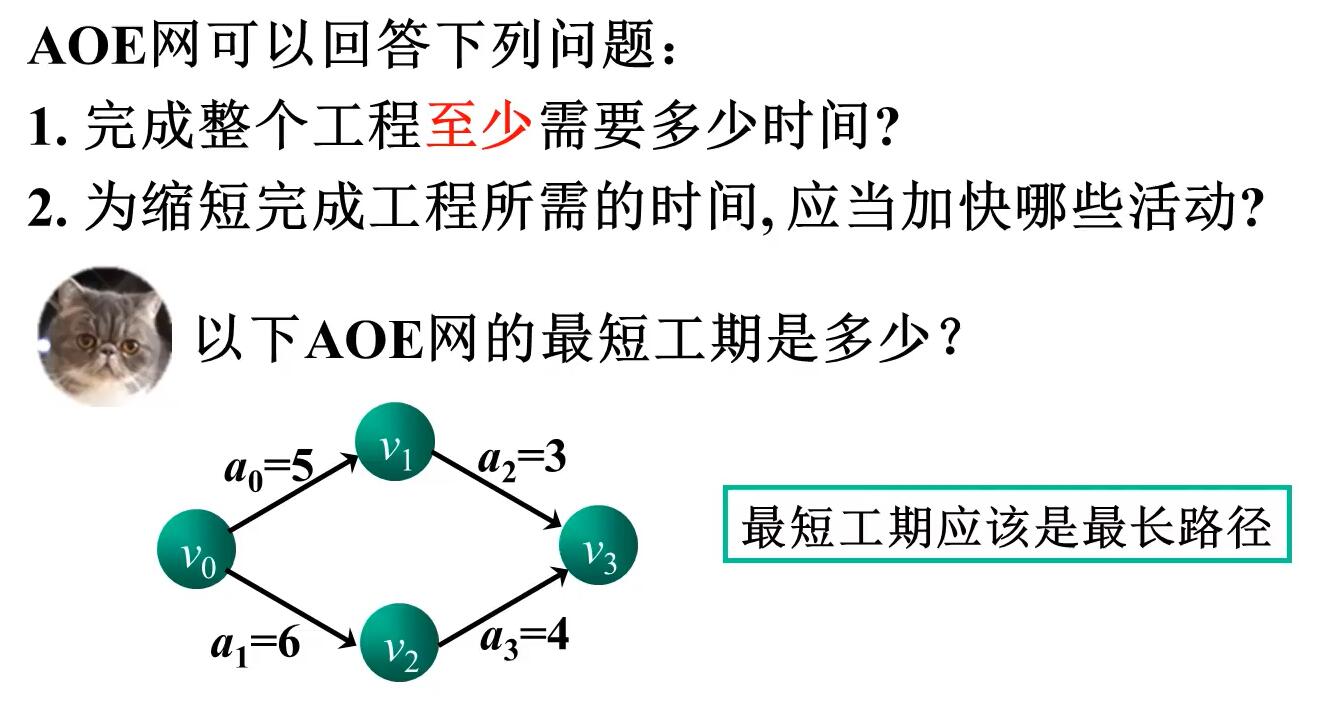
关键路径

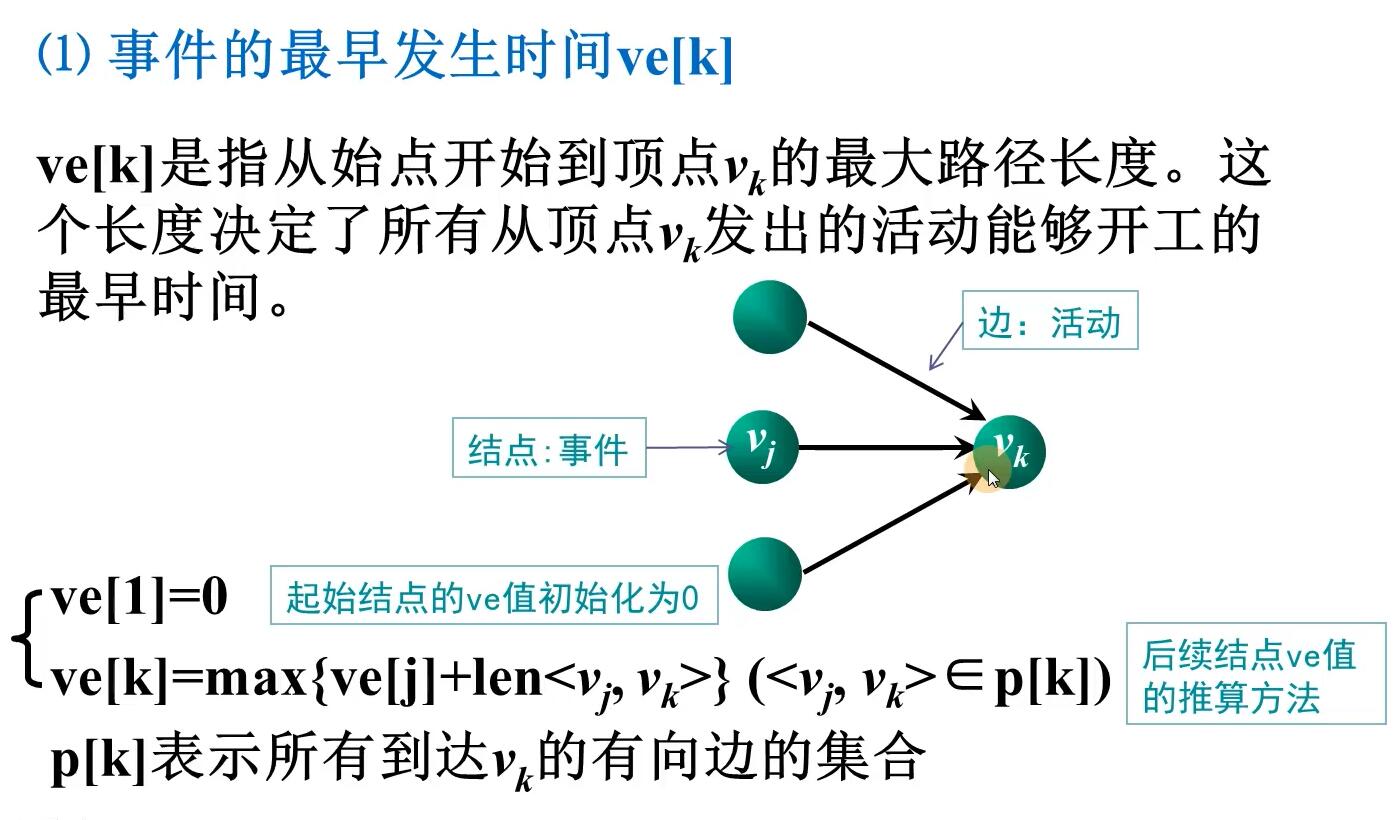
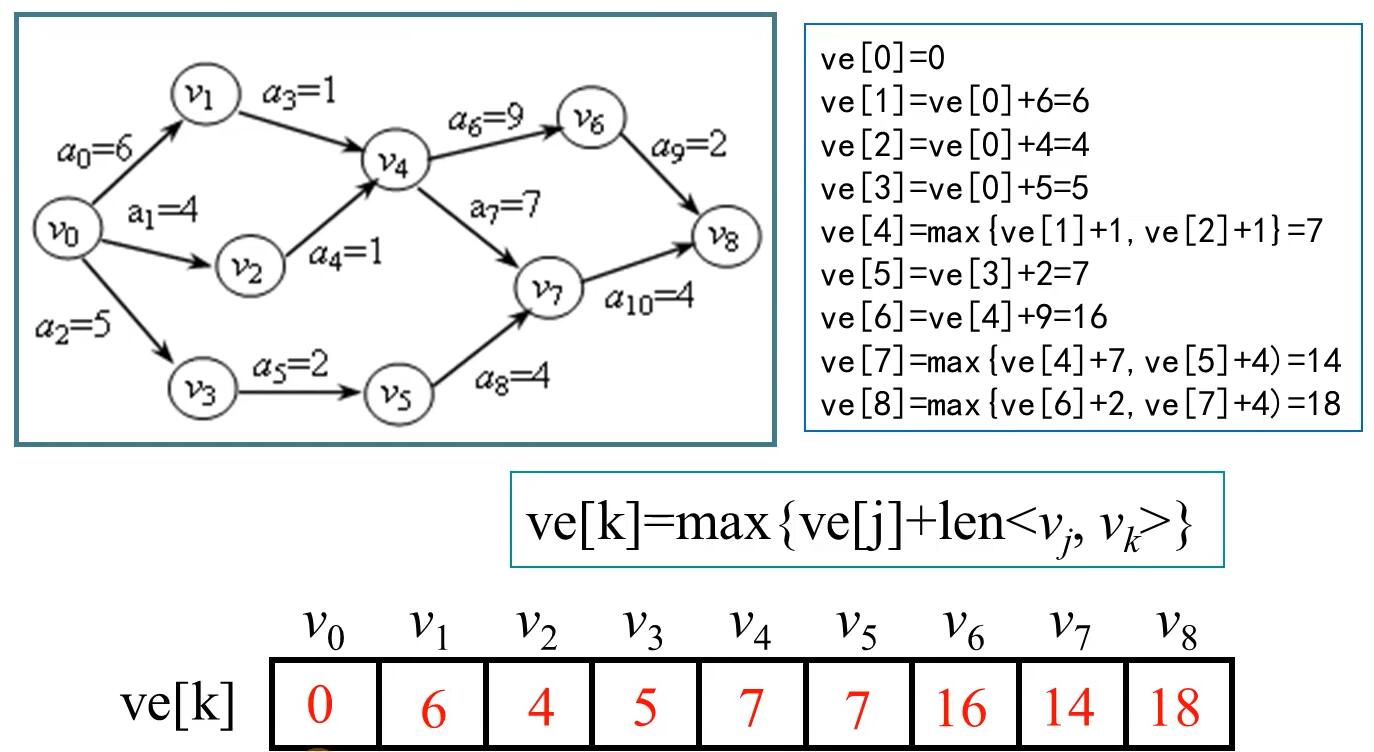
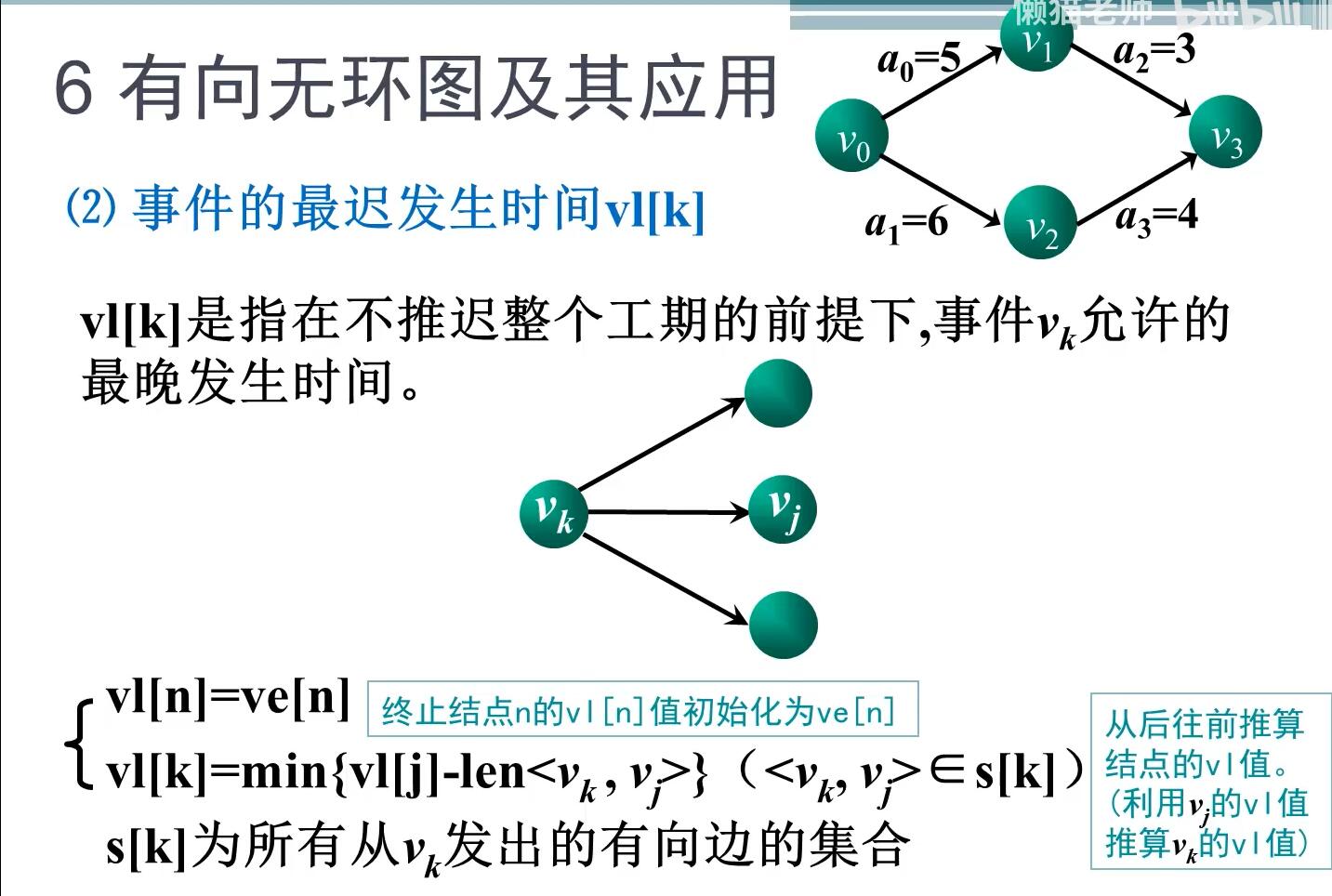
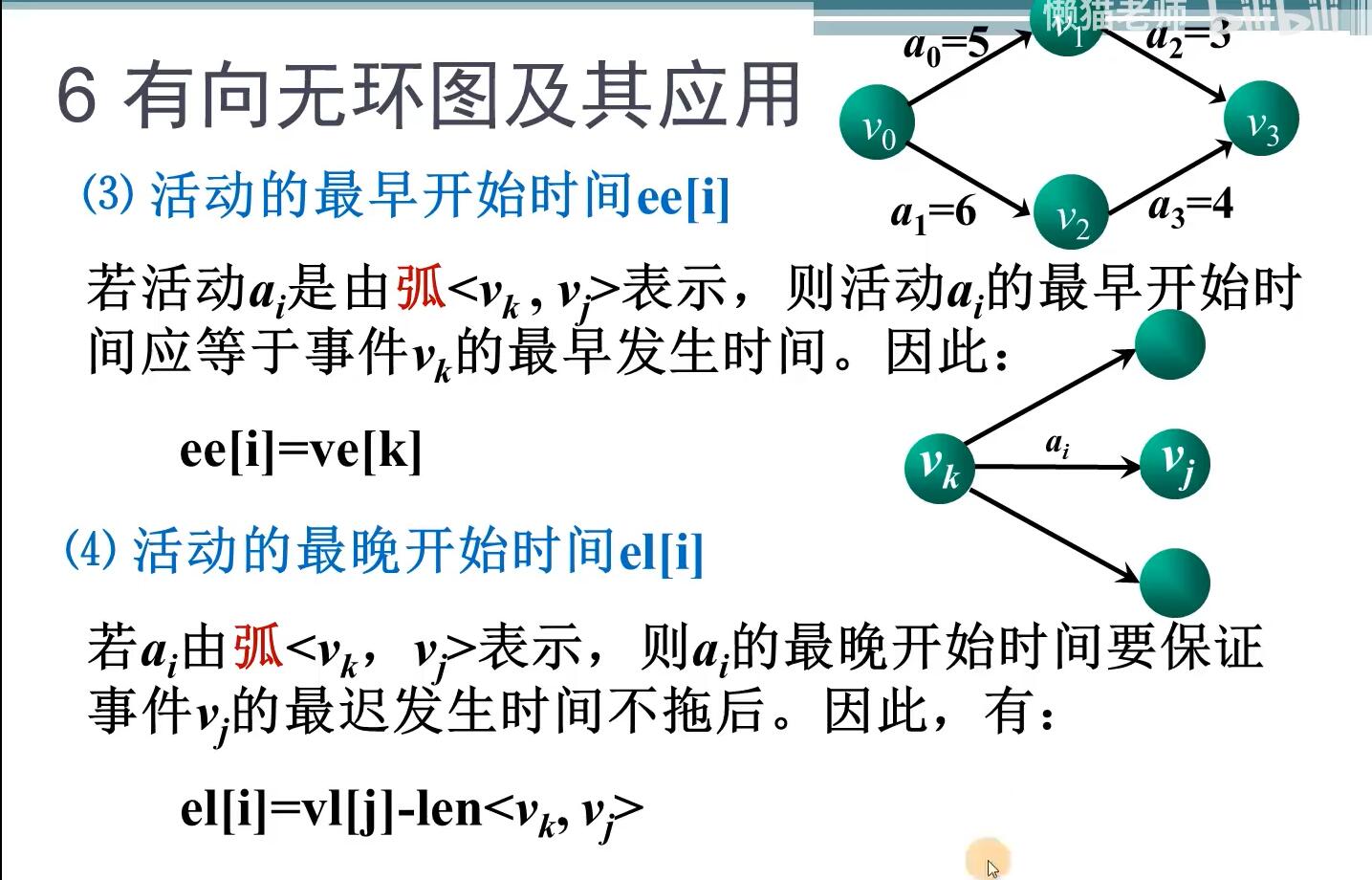
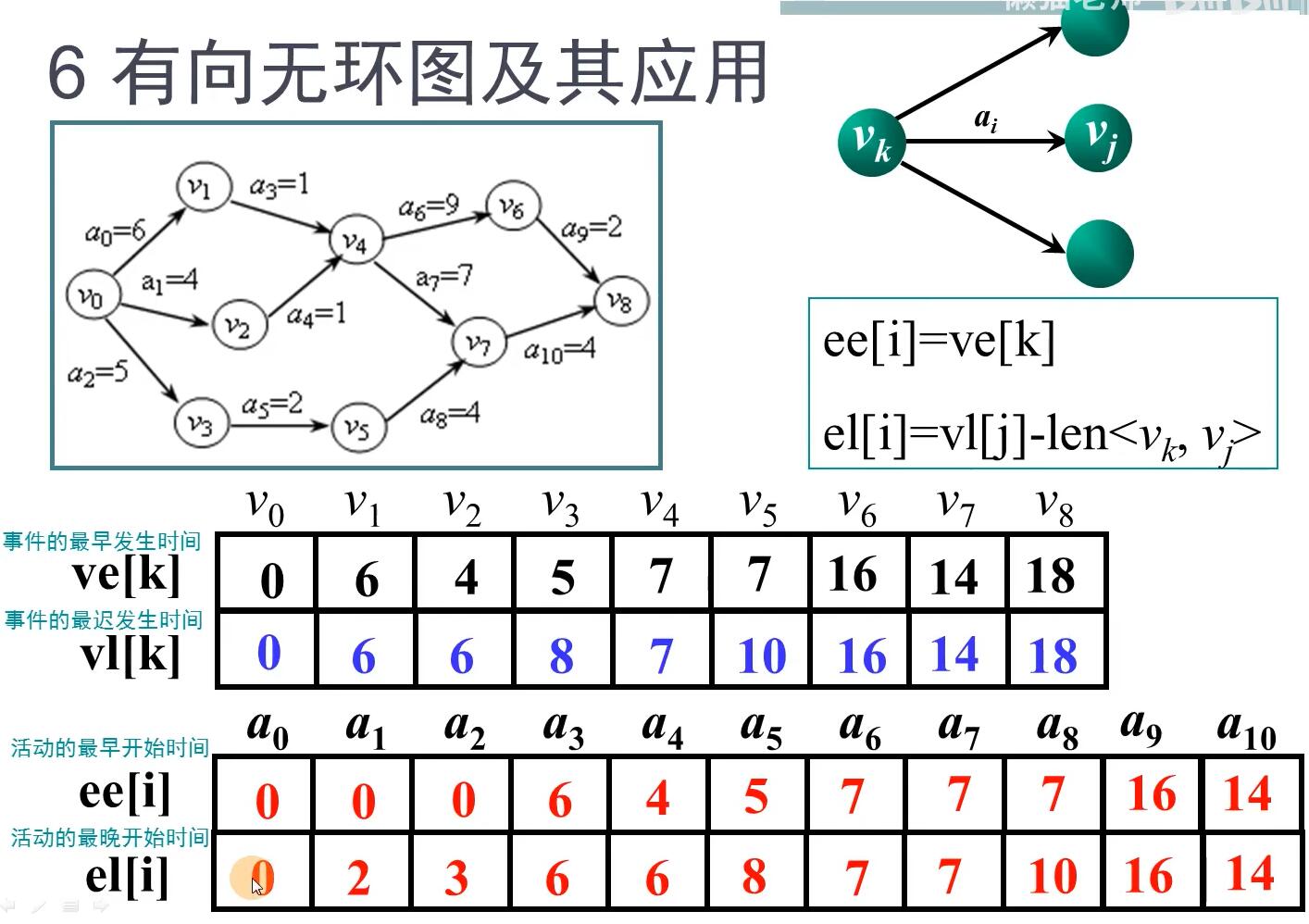
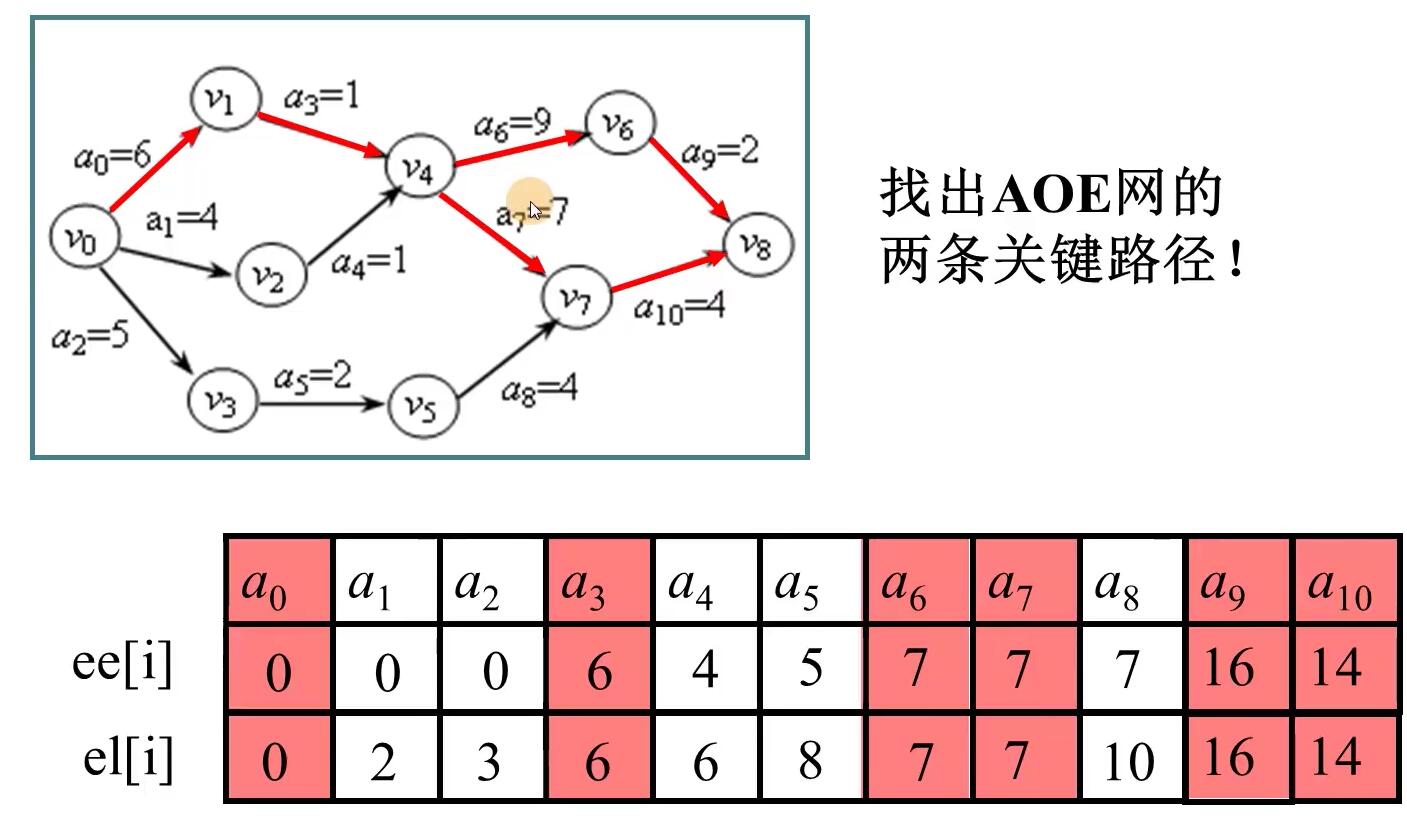
数据结构

核心代码

TopologicalSort

/*
    TopologicalSort用于实现拓扑排序
    参数：result用来保存处理过的拓扑排序顶点；count用来保存处理过的拓扑排序顶点的个数
    功能：进行拓扑排序，将找到的拓扑顶点序号存入result数组（result可以看成一个栈,count可以看成是栈顶指针）
          增加的功能：用注释=====标识，在拓扑排序的同时计算ve数组的值[事件最早发生时间]
*/
bool ALGraph ::TopologicalSort(int result[], int &count){

    int stack[MAX_VERTEX];   //把顶点对应的下标压入堆栈

    int top = -1;
    int inVex; //用来保存从堆栈中弹出的顶点（下标）[书上的j，代表一个边的起始顶点]
    int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点[书上的k，代表一个边的终止顶点]
    ArcNode *p;

    //初始化事件最早发生时间ve数组=====
    for(int i=0;i<vertexNum;i++){
        ve[i]=0;
    }
    //遍历顶点表，把入度为0的压栈
    for(int i=0;i<vertexNum;i++){
        if(adjList[i].in==0){
            stack[++top]=i;
        }
    }
    //完成拓扑排序
    count=0;
    while(top!=-1){
        inVex=stack[top--];
        result[count]=inVex;
        count++;
        p=adjList[inVex].firstEdge;
        while(p){
            outVex=p->adjvex;
            adjList[outVex].in--;
            if(adjList[outVex].in==0)
                stack[++top]=outVex;
            if(ve[inVex]+p->weight>ve[outVex])
                ve[outVex]=ve[inVex]+p->weight;
            p=p->next;
        }
    }
    //判断拓扑排序是否正确
    if(count==vertexNum)
        return true;
    return false;
}

CriticalPath

/*
    CriticalPath用于求关键路径
    首先调用TopologicalSort函数检查是否是一个没有环的图
*/
bool ALGraph::CriticalPath(){

    int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
    int resultTop;               //拓扑排序有效顶点个数(栈顶指针)
    ArcNode *p;
    int i,count;
    int inVex,outVex;   //inVex,outVex，分别代表一条边的起点顶点号和终点顶点号

    if(!TopologicalSort(resultStack,count)) {
        return false;
    }

    //输出拓扑排序的顶点处理顺序
    cout<<"拓扑排序的顶点处理顺序是："<<endl;
    for(int i=0;i<count;i++){
        cout<<resultStack[i]<<" ";
    }
    cout<<endl;
    //输出ve数组的值
    cout<<"ve数组的值为："<<endl;
    for(int i=0;i<count;i++){
        cout<<"ve["<<i<<"]="<<ve[i]<<endl;
    }
    //完成关键路径的求解
    resultTop=count-1;
    inVex=resultStack[resultTop--];
    for(int i=0;i<vertexNum;i++){
        vl[i]=ve[inVex];
    }
    while(resultTop!=-1){
        inVex=resultStack[resultTop--];
        p=adjList[inVex].firstEdge;
        while(p){
            outVex=p->adjvex;
            if(vl[inVex]>vl[outVex]-p->weight)
                vl[inVex]=vl[outVex]-p->weight;
            p=p->next;
        }
    }
    cout<<"vl数组的值为："<<endl;
    for(int i=0;i<count;i++){
        cout<<"vl["<<i<<"]="<<vl[i]<<endl;
    }
    return true;
}

完整代码

#include <iostream>
#include <stdio.h>
using namespace std;

const int MAX_VERTEX = 30;    //图的最大顶点数

struct ArcNode  /*边表*/
{
    int weight;     //增加权值分量，代表活动时间=====
    int adjvex;
    ArcNode *next;
};

struct VertexNode  /*顶点表*/
{
    int in;                //增加入度字段-----
    char vertex;
    ArcNode *firstEdge;
};

class ALGraph {
private:
    VertexNode *adjList;  //邻接表
    int vertexNum, arcNum;
    int *ve, *vl; //ve数组是事件最早发生时间，vl事件最迟发生时间(数组长度跟顶点数相等)=====
public:
    ALGraph(char v[], int n, int e);
    ~ALGraph();
    void inputEdges();
    bool setEdge(int vi,int vj,int weight);
    void displayData();

    bool TopologicalSort(int result[], int &count); //拓扑排序
    bool CriticalPath();   //求关键路径
};

ALGraph:: ALGraph(char v[], int n, int e){
    vertexNum = n;
    arcNum = e;
    adjList = new VertexNode[vertexNum];
    for (int i=0; i<vertexNum; i++) {
        //输入顶点信息，初始化顶点表
        adjList[i].in = 0;    //增加in的初始化-----
        adjList[i].vertex = v[i];
        adjList[i].firstEdge = NULL;
    }
    ve = new int[vertexNum];
    vl = new int[vertexNum];

}
ALGraph ::~ALGraph(){
    ArcNode *p,*pre;
    //遍历顶点表数组，把顶点表指向的所有边结点删除
    for(int i=0; i<vertexNum; i++){
        p = adjList[i].firstEdge;
        adjList[i].firstEdge = NULL;
        while(p){
            pre = p;
            p = p-> next;
            delete pre;
        }
    }
    delete [] adjList;
    delete [] ve;
    delete [] vl;
}

void ALGraph  ::inputEdges(){  //=====
    cout << "请输入两个事件顶点编号(范围0-"<< vertexNum-1 << ")和活动时间:"<<endl;
    for (int i=0; i<arcNum; i++) {
         //输入边的信息存储在边表中
        int vi,vj, weight;
        cin >> vi >> vj >> weight;   //输入边依附的两个顶点的编号
        if(!setEdge(vi,vj,weight)){
            cout << "输入的顶点编号超过范围或者相等，需要重新输入" << endl;
            i--;
        }
    }
}

bool ALGraph::setEdge(int vi,int vj, int weight){  //=====
    //修改setEdge函数，把vj顶点表中的入度+1 -----
    ArcNode *s;
    if (vi>=0 && vi<vertexNum && vj>=0 && vj<vertexNum && vi!=vj){
        //创建一个边结点vj
        s = new ArcNode;
        s->adjvex = vj;
        s->weight = weight; //=====
        //把边结点vj插入到顶点表vi项的邻接表中，成为第一个结点
        s->next = adjList[vi].firstEdge;
        adjList[vi].firstEdge = s;
        //vj顶点表中的入度+1   -----
        adjList[vj].in++;
        return true;
    }
    else {
        return false;
    }
}

void ALGraph ::displayData(){
    ArcNode *p;
     cout << "输出图的存储情况："<<endl;
    for(int i=0; i<vertexNum; i++){
        cout << "顶点" << adjList[i].vertex << "的入度为：" << adjList[i].in <<"，从这个顶点发出的的边为：" << endl;//-----
        p = adjList[i].firstEdge;
        if (!p)
            cout << "没有。"<< endl;
        while(p){
            cout <<"<" << i <<"," << p->adjvex<< ">" << p->weight <<endl;
            p = p->next;
        }
    }
}
/*
    TopologicalSort用于实现拓扑排序
    参数：result用来保存处理过的拓扑排序顶点；count用来保存处理过的拓扑排序顶点的个数
    功能：进行拓扑排序，将找到的拓扑顶点序号存入result数组（result可以看成一个栈,count可以看成是栈顶指针）
          增加的功能：用注释=====标识，在拓扑排序的同时计算ve数组的值[事件最早发生时间]
*/
bool ALGraph ::TopologicalSort(int result[], int &count){

    int stack[MAX_VERTEX];   //把顶点对应的下标压入堆栈

    int top = -1;
    int inVex; //用来保存从堆栈中弹出的顶点（下标）[书上的j，代表一个边的起始顶点]
    int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点[书上的k，代表一个边的终止顶点]
    ArcNode *p;

    //初始化事件最早发生时间ve数组=====
    for(int i=0;i<vertexNum;i++){
        ve[i]=0;
    }
    //遍历顶点表，把入度为0的压栈
    for(int i=0;i<vertexNum;i++){
        if(adjList[i].in==0){
            stack[++top]=i;
        }
    }
    //完成拓扑排序
    count=0;
    while(top!=-1){
        inVex=stack[top--];
        result[count]=inVex;
        count++;
        p=adjList[inVex].firstEdge;
        while(p){
            outVex=p->adjvex;
            adjList[outVex].in--;
            if(adjList[outVex].in==0)
                stack[++top]=outVex;
            if(ve[inVex]+p->weight>ve[outVex])
                ve[outVex]=ve[inVex]+p->weight;
            p=p->next;
        }
    }
    //判断拓扑排序是否正确
    if(count==vertexNum)
        return true;
    return false;
}

/*
    CriticalPath用于求关键路径
    首先调用TopologicalSort函数检查是否是一个没有环的图
*/
bool ALGraph::CriticalPath(){

    int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
    int resultTop;               //拓扑排序有效顶点个数(栈顶指针)
    ArcNode *p;
    int i,count;
    int inVex,outVex;   //inVex,outVex，分别代表一条边的起点顶点号和终点顶点号

    if(!TopologicalSort(resultStack,count)) {
        return false;
    }

    //输出拓扑排序的顶点处理顺序
    cout<<"拓扑排序的顶点处理顺序是："<<endl;
    for(int i=0;i<count;i++){
        cout<<resultStack[i]<<" ";
    }
    cout<<endl;
    //输出ve数组的值
    cout<<"ve数组的值为："<<endl;
    for(int i=0;i<count;i++){
        cout<<"ve["<<i<<"]="<<ve[i]<<endl;
    }
    //完成关键路径的求解
    resultTop=count-1;
    inVex=resultStack[resultTop--];
    for(int i=0;i<vertexNum;i++){
        vl[i]=ve[inVex];
    }
    while(resultTop!=-1){
        inVex=resultStack[resultTop--];
        p=adjList[inVex].firstEdge;
        while(p){
            outVex=p->adjvex;
            if(vl[inVex]>vl[outVex]-p->weight)
                vl[inVex]=vl[outVex]-p->weight;
            p=p->next;
        }
    }
    cout<<"vl数组的值为："<<endl;
    for(int i=0;i<count;i++){
        cout<<"vl["<<i<<"]="<<vl[i]<<endl;
    }
    return true;
}

int main(){
    char vertex[MAX_VERTEX];
    int num,edge;

    cout << "请输入顶点个数和边的个数：";
    cin >> num >> edge;
    for(int i=0; i<num; i++)
        vertex[i] = i + '0';

    ALGraph graph(vertex,num,edge);
    graph.inputEdges();
    graph.displayData();

    if(!graph.CriticalPath()){
        cout << "这个图有回路，不能求关键路径。";
    }

    //记住，main函数调用结束后，会自动调用析构函数，对图的数据以及ve，vl数组进行释放。

    return 0;
}

输入：

9 11
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4

输出：

输出图的存储情况：
顶点0的入度为：0，从这个顶点发出的的边为：
<0,3>5
<0,2>4
<0,1>6
顶点1的入度为：1，从这个顶点发出的的边为：
<1,4>1
顶点2的入度为：1，从这个顶点发出的的边为：
<2,4>1
顶点3的入度为：1，从这个顶点发出的的边为：
<3,5>2
顶点4的入度为：2，从这个顶点发出的的边为：
<4,7>7
<4,6>9
顶点5的入度为：1，从这个顶点发出的的边为：
<5,7>4
顶点6的入度为：1，从这个顶点发出的的边为：
<6,8>2
顶点7的入度为：2，从这个顶点发出的的边为：
<7,8>4
顶点8的入度为：2，从这个顶点发出的的边为：
没有。
拓扑排序的顶点处理顺序是：
0 1 2 4 6 3 5 7 8
ve数组的值为：
ve[0]=0
ve[1]=6
ve[2]=4
ve[3]=5
ve[4]=7
ve[5]=7
ve[6]=16
ve[7]=14
ve[8]=18
vl数组的值为：
vl[0]=0
vl[1]=6
vl[2]=6
vl[3]=8
vl[4]=7
vl[5]=10
vl[6]=16
vl[7]=14
vl[8]=18