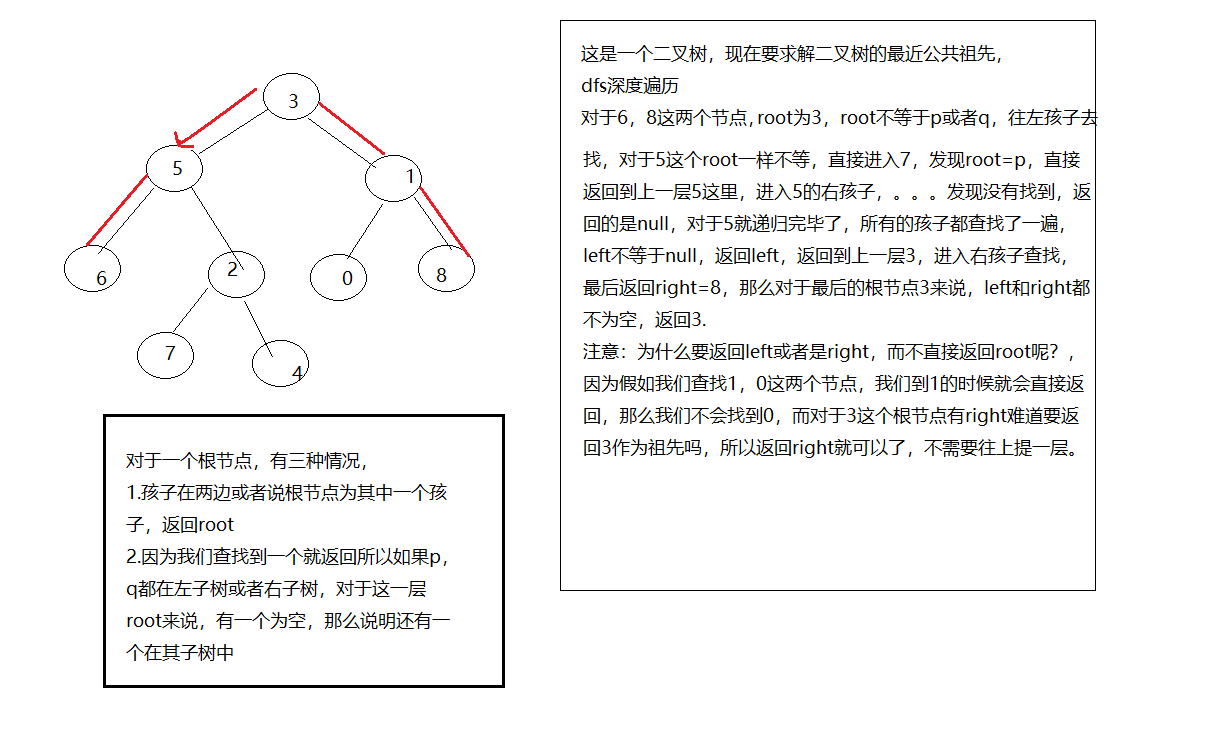
lca(lowestCommonAncestor)的更多相关文章

  1. 1151 LCA in a Binary Tree (30point(s))

    The lowest common ancestor (LCA) of two nodes U and V in a tree is the deepest node that has both U ...

  2. LeetCode Day3

     Lowest Common Ancestor of a Binary Search Tree import java.util.ArrayList; import java.util.List; / ...

  3. Summary: Lowest Common Ancestor in a Binary Tree & Shortest Path In a Binary Tree

    转自:Pavel's Blog Now let's say we want to find the LCA for nodes 4 and 9, we will need to traverse th ...

  4. LCA of a Binary Tree

    236. Lowest Common Ancestor of a Binary Tree /** * 基础版 * 给定p,q都是在树中 * 有两种情况: * 1. p和q分布在LCA的两侧 * 2. ...

  5. poj 1330 Nearest Common Ancestors（LCA：最近公共祖先）

    多校第七场考了一道lca,那么就挑一道水题学习一下吧= = 最简单暴力的方法:建好树后,输入询问的点u,v,先把u全部的祖先标记掉,然后沿着v->rt(根)的顺序检查,第一个被u标记的点即为u, ...

  6. LeetCode Lowest Common Ancestor of a Binary Search Tree （LCA最近公共祖先）

    题意: 给一棵二叉排序树,找p和q的LCA. 思路: 给的是BST(无相同节点),那么每个节点肯定大于左子树中的最大,小于右子树种的最小.根据这个特性,找LCA就简单多了. 分三种情况: (1)p和q ...

  7. 查找最近公共祖先(LCA)

    一.问题 求有根树的任意两个节点的最近公共祖先(一般来说都是指二叉树).最近公共祖先简称LCA(Lowest Common Ancestor).例如,如下图一棵普通的二叉树. 结点3和结点4的最近公共 ...

  8. 利用Tarjan算法解决（LCA）二叉搜索树的最近公共祖先问题——数据结构

    相关知识:(来自百度百科)  LCA(Least Common Ancestors) 即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先. 例如: 1和7的最近公共祖先为5: 1和5的 ...

  9. 面试题6：二叉树最近公共节点（LCA）《leetcode236》

    Lowest Common Ancestor of a Binary Tree(二叉树的最近公共父亲节点) Given a binary tree, find the lowest common an ...

随机推荐

  1. pyside2安装避坑

    cmd 输入 pip install PySide2 官方下载太慢 清华源: pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pysid ...

  2. Qlik Sense插件及QRS接口补充

    date: 2019-10-18 09:10:00 updated: 2019-10-18 15:18:00 Qlik Sense插件及QRS接口补充 1.插件 1.1 获取数据方式 理论上 Engi ...

  3. 02 . Go框架之Gin框架从入门到熟悉(数据解析和绑定,渲染,重定向,同步异步,中间件)

    数据解析和绑定 json数据解析和绑定 package main import ( "github.com/gin-gonic/gin" "net/http" ...

  4. PHP定界符的用法

    当面临大段的负责的文本输入的时候,建议使用定界符. 例如: $age = 28; $str = <<<cont 第一行数据 第二行数据 特殊字符 ' " asdf abc ...

  5. freopen （）函数

    1.格式 FILE * freopen ( const char * filename, const char * mode, FILE * stream ); 2.参数说明 filename: 要打 ...

  6. Kubernetes YAML最佳实践和策略

    Kubernetes工作负载最常用YAML格式的文件来定义. YAML的问题之一就是很难描述清单文件之间的约束或关系. 如果你希望检查是否已从受信任的注册表中提取部署到群集中的所有映像,该怎么办? 如 ...

  7. Python彩蛋、字典、列表高级用法、元类、混入、迭代器、生成器、生成式、git

    一.类与类的关系 关注公众号"轻松学编程"了解更多. is-a 继承 继承是指一个类(称为子类.子接口)继承另外一个类(称为父类.父接口)的功能, 并可以增加它自己的新功能的能力. ...

  8. python开发基础(二)运算符以及数据类型之int(数字)

    # encoding: utf-8 # module builtins # from (built-in) # by generator 1.147 """ Built- ...

  9. 1.深入Istio：Sidecar自动注入如何实现的？

    转载请声明出处哦~,本篇文章发布于luozhiyun的博客:https://www.luozhiyun.com 本文使用的Istio源码是 release 1.5. 这篇文章打算讲一下sidecar, ...

  10. MySQL全面瓦解9：查询的排序、分页相关

    概述 数据库中的数据直接呈现出来一般不是我们想要的,所以我们上两节演示了如何对数据进行过滤的方法.除了对数据进行过滤, 我们可能还需要对数据进行排序,比如想从列表中了解消费最高的项,就可能需要对金额字 ...