做一个logitic分类之鸢尾花数据集的分类

Iris 鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种。

首先我们来加载一下数据集。同时大概的展示下数据结构和数据摘要。

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

data = pd.read_csv('./data/iris.csv')

print(data.head())

print(data.info())

print(data['Species'].unique())

   Unnamed: 0  Sepal.Length  Sepal.Width  Petal.Length  Petal.Width Species

0           1           5.1          3.5           1.4          0.2  setosa

1           2           4.9          3.0           1.4          0.2  setosa

2           3           4.7          3.2           1.3          0.2  setosa

3           4           4.6          3.1           1.5          0.2  setosa

4           5           5.0          3.6           1.4          0.2  setosa

<class 'pandas.core.frame.DataFrame'>

RangeIndex: 150 entries, 0 to 149

Data columns (total 6 columns):

Unnamed: 0      150 non-null int64

Sepal.Length    150 non-null float64

Sepal.Width     150 non-null float64

Petal.Length    150 non-null float64

Petal.Width     150 non-null float64

Species         150 non-null object

dtypes: float64(4), int64(1), object(1)

memory usage: 7.2+ KB

None

['setosa' 'versicolor' 'virginica']

通过上述数据的简单摘要，我们可以得到鸢尾花一共有三类：

setosa
versicolor
virginica

我们分别用0,1,2来表示['setosa' 'versicolor' 'virginica']

整理

首先，我们对数据集进行一个简单的整理。我们需要把分类替换成0,1,2

其次，我们把数据集分成两个分类，一个用来训练我们的logitic算法的参数，另外一个用来测试我们的训练的结果

以下是代码：

# 数值替换

data.loc[data['Species']=='setosa','Species']=0

data.loc[data['Species']=='versicolor','Species']=1

data.loc[data['Species']=='virginica','Species']=2

print(data)

     Unnamed: 0  Sepal.Length  Sepal.Width  Petal.Length  Petal.Width  Species

0             1           5.1          3.5           1.4          0.2        0

1             2           4.9          3.0           1.4          0.2        0

2             3           4.7          3.2           1.3          0.2        0

3             4           4.6          3.1           1.5          0.2        0

4             5           5.0          3.6           1.4          0.2        0

..          ...           ...          ...           ...          ...      ...

145         146           6.7          3.0           5.2          2.3        2

146         147           6.3          2.5           5.0          1.9        2

147         148           6.5          3.0           5.2          2.0        2

148         149           6.2          3.4           5.4          2.3        2

149         150           5.9          3.0           5.1          1.8        2

[150 rows x 6 columns]

#分割训练集和测试集

train_data = data.sample(frac=0.6,random_state=0,axis=0)

test_data = data[~data.index.isin(train_data.index)]

train_data = np.array(train_data)

test_data = np.array(test_data)

train_label = train_data[:,5:6].astype(int)

test_label = test_data[:,5:6].astype(int)

print(train_label[:1])

print(test_label[:1])

train_data = train_data[:,1:5]

test_data = test_data[:,1:5]

print(np.shape(train_data))

print(np.shape(train_label))

print(np.shape(test_data))

print(np.shape(test_label))

[[2]]

[[0]]

(90, 4)

(90, 1)

(60, 4)

(60, 1)

我们需要把label编程1ofN的样式

经过上述两步的操作，我们可以看到数据集被分成两个部分。我们接下来对数据进行logitic分类。

train_label_onhot = np.eye(3)[train_label]

test_label_onhot = np.eye(3)[test_label]

train_label_onhot = train_label_onhot.reshape((90,3))

test_label_onhot =  test_label_onhot.reshape((60,3))

print(train_label_onhot[:3])

[[0. 0. 1.]

 [0. 1. 0.]

 [1. 0. 0.]]

分类

思路

我选选择先易后难的方法来处理这个问题：

如果我们有两个分类0或者1的话，我们需要判断特征值X（N维）是否可以归为某个分类。我们的步骤如下:

初始化参数w（1，N）和b(1)
计算 \(z = \sum_{i=0}^{n}w*x + b\)
带入\(\sigma\)函数得到\(\hat{y}=\sigma(z)\)

现在有多个分类, 我们就需要使用one-to-many的方法去计算。简单的理解，在本题中，一共有3个分类。我们需要计算\(\hat{y}_1\)来表明这个东西是分类1或者不是分类1的概率 \(\hat{y}_2\)是不是分类2的概率，\(\hat{y}_3\)是不是分类3的概率。然后去比较这三个分类那个概率最大，就是哪个的概率。

比较属于哪个概率大的算法，我们用softmat。就是计算\(exp(\hat{y}_1)\),\(exp(\hat{y}_2)\),\(exp(\hat{y}_3)\),然后得到属于三个分类的概率分别是

p1=\(\frac{exp(\hat{y}_1)}{\sum_{i=0}{3}(\hat{y}_i)}\)
p1=\(\frac{exp(\hat{y}_2)}{\sum_{i=0}{3}(\hat{y}_i)}\)
p1=\(\frac{exp(\hat{y}_3)}{\sum_{i=0}{3}(\hat{y}_i)}\)

我们根据上述思想去计算一条记录,代码如下:

def sigmoid(s):

     return 1. / (1 + np.exp(-s))

w = np.random.rand(4,3)

b = np.random.rand(3)

def get_result(w,b):

    z = np.matmul(train_data[0],w) +b

    y = sigmoid(z)

    return y

y = get_result(w,b)

print(y)

[0.99997447 0.99966436 0.99999301]

上述代码是我们只求一条记录的代码，下面我们给他用矩阵化修改为一次计算全部的训练集的\(\hat{y}\)

def get_result_all(data,w,b):

    z = np.matmul(data,w)+ b

    y = sigmoid(z)

    return y

y=get_result_all(train_data,w,b)

print(y[:10])

[[0.99997447 0.99966436 0.99999301]

 [0.99988776 0.99720719 0.9999609 ]

 [0.99947512 0.98810796 0.99962362]

 [0.99999389 0.99980632 0.999999  ]

 [0.9990065  0.98181945 0.99931113]

 [0.99999094 0.9998681  0.9999983 ]

 [0.99902719 0.98236513 0.99924728]

 [0.9999761  0.99933525 0.99999313]

 [0.99997542 0.99923594 0.99999312]

 [0.99993082 0.99841774 0.99997519]]

接下来我们要求得一个损失函数，来计算我们得到的参数和实际参数之间的偏差，关于分类的损失函数，请看这里

单个分类的损失函数如下：

\[loss=−\sum_{i=0}^{n}[y_iln\hat{y}_i+(1−y_i)ln(1−\hat{y}_i)]
\]

损失函数的导数求法如下

当 \(y_i=0\)时

w的导数为：

\[\frac{dloss}{dw}=(1-y_i)*\frac{1}{1-\hat{y}_i}*\hat{y}_i*(1-\hat{y}_i)*x_i
\]

化简得到

\[\frac{dloss}{dw}=\hat{y}*x_i=(\hat{y}-y)*x_i
\]

b的导数为

\[\frac{dloss}{db}=(1-y_i)*\frac{1}{1-\hat{y}_i}*\hat{y}_i*(1-\hat{y}_i)
\]

化简得到

\[\frac{dloss}{db}=\hat{y}-y
\]

当\(y_i\)=1时

w的导数

\[\frac{dloss}{dw}=-yi*\frac{1}{\hat{y}}*\hat{y}(1-\hat{y})*x_i
\]

化简

\[\frac{dloss}{dw}=(\hat{y}-1)*x_i=(\hat{y}-y)*x_i
\]

b的导数

\[\frac{dloss}{dw}=\hat{y}-y
\]

综合起来可以得到

\[\frac{dloss}{dw}=\sum_{i=0}^{n}(\hat{y}-y)*x_i
\]

\[\frac{dloss}{db}=\sum_{i=0}^{n}(\hat{y}-y)
\]

我们只需要根据以下公式不停的调整w和b,就是机器学习的过程

\[w=w-learning_rate*dw
\]

\[b=b-learning_rate*db
\]

下面我们来写下代码：

learning_rate = 0.0001

def eval(data,label, w,b):

    y = get_result_all(data,w,b)

    y = y.argmax(axis=1)

    y = np.eye(3)[y]

    count = np.shape(data)[0]

    acc = (count - np.power(y-label,2).sum()/2)/count

    return acc

def train(step,w,b):

    y = get_result_all(train_data,w,b)

    loss = -1*(train_label_onhot * np.log(y) +(1-train_label_onhot)*np.log(1-y)).sum()

    dw = np.matmul(np.transpose(train_data),y - train_label_onhot)

    db = (y - train_label_onhot).sum(axis=0)

    w = w - learning_rate * dw

    b = b - learning_rate * db

    return w, b,loss

loss_data = {'step':[],'loss':[]}

train_acc_data = {'step':[],'acc':[]}

test_acc_data={'step':[],'acc':[]}

for step in range(3000):

    w,b,loss = train(step,w,b)

    train_acc = eval(train_data,train_label_onhot,w,b)

    test_acc = eval(test_data,test_label_onhot,w,b)

    loss_data['step'].append(step)

    loss_data['loss'].append(loss)

    train_acc_data['step'].append(step)

    train_acc_data['acc'].append(train_acc)

    test_acc_data['step'].append(step)

    test_acc_data['acc'].append(test_acc)

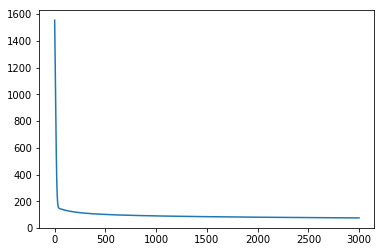
plt.plot(loss_data['step'],loss_data['loss'])

plt.show()

plt.plot(train_acc_data['step'],train_acc_data['acc'],color='red')

plt.plot(test_acc_data['step'],test_acc_data['acc'],color='blue')

plt.show()

print(test_acc_data['acc'][-1])

![png]

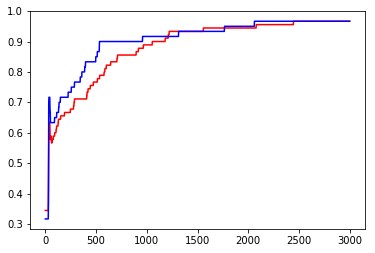
0.9666666666666667

从上述运行结果中来看，达到了96.67%的预测准确度。还不错！