关于直线，V形线，Z形线，M形线分割平面的总结

一：N条直线分割平面

假设，x条线能将平面分为f(x)份，这对于份f(n) 第n条线，和其他n-1条线都有交点时，增加量最大，为n;

则： f(n)=f(n-1)+n;

有f(0)=1；得到：n 条直线分割平面的数量最大为：f(n)=n*(n+1)/2 + 1;

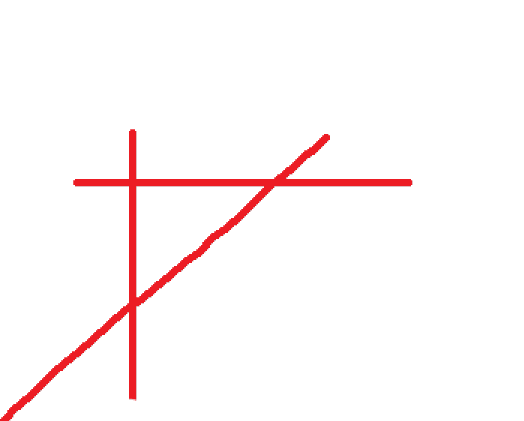
二. “V” 形线分割平面

对于“V”,我们可以把他们当成两条相交直线去掉两条射线。如下图：

上图为两条‘V’形线，对于每条‘V’形线，都相当于两条直线去掉后面两天射线，二去掉这两条射线会使平面减少2，

一因此，有直线公式转化得到： F(n)=f(2n)-2n=2n(2n+1)/2+1-2n;

三.  'N'形线

‘N’形线份两种，一种是有两条平行边，二是没有平行边；

对于没有平行边的情况吧，推导过程和‘V’形线相似，

我们可以将其看成3条直线相交，然后去掉4条射线，去掉这4条射线后，会使平面相对于3条直线减少6；

有直线公式颗推得：

f(N)=f(3n)-6n=3n(3n+1)/2+1-6n;

如果是有平行,得情况则相对于没有的情况减少一个平面；

即为： f(N)=f(3n)=3n(3n+1)/2 + 1 - 5n;