形象解释各种卷积算法(Convolution animations)
 |
 |
 |
 |
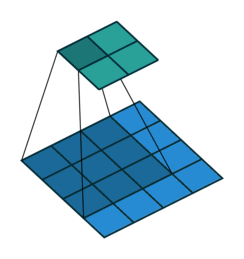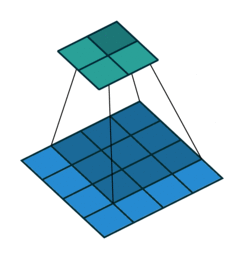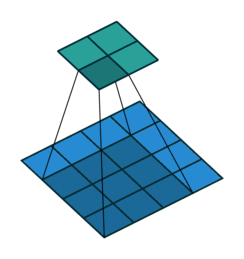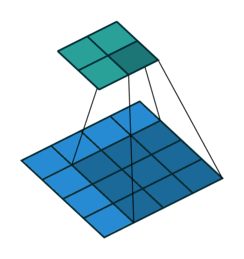
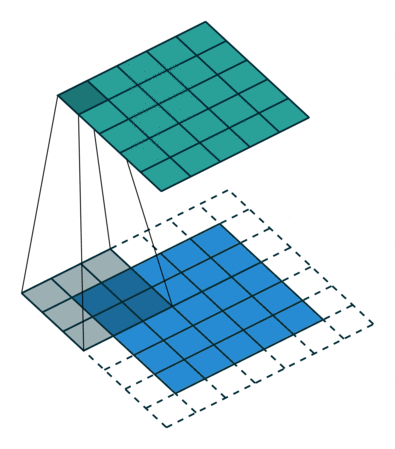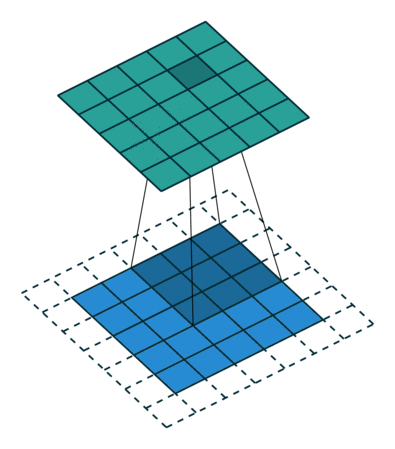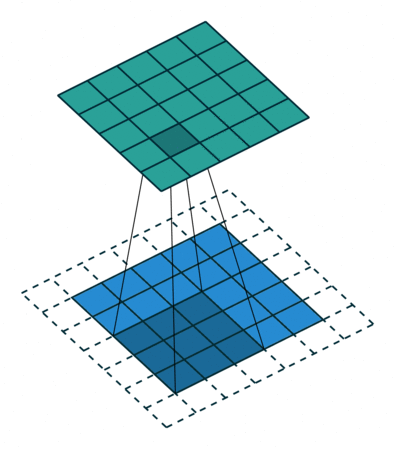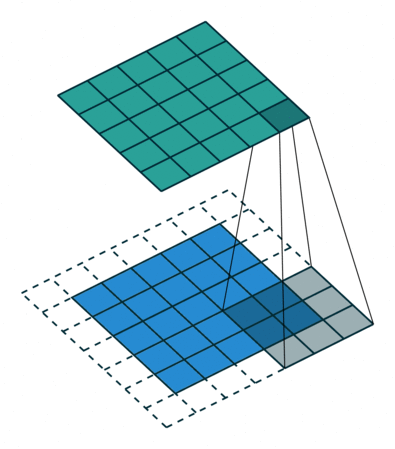
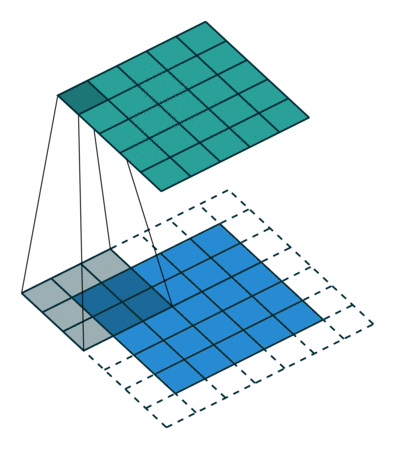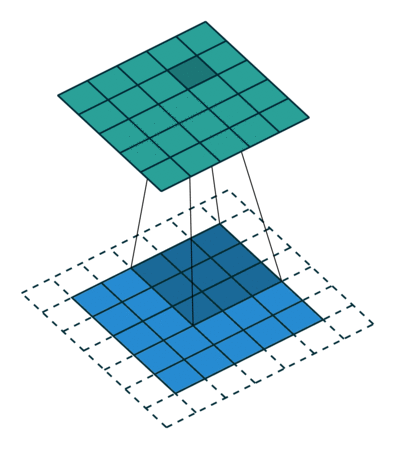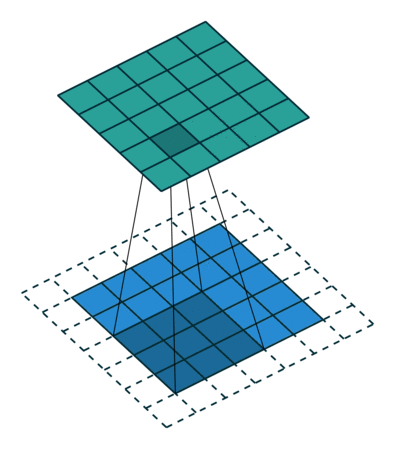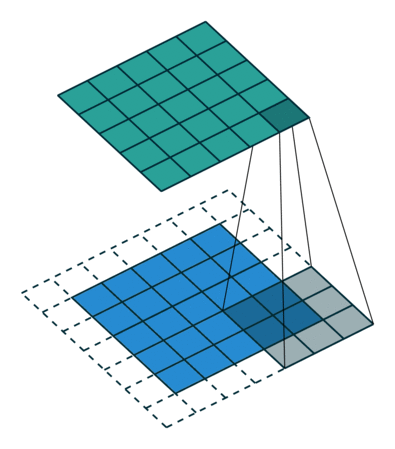
| No padding, no strides | Arbitrary padding, no strides | Half padding, no strides | Full padding, no strides |
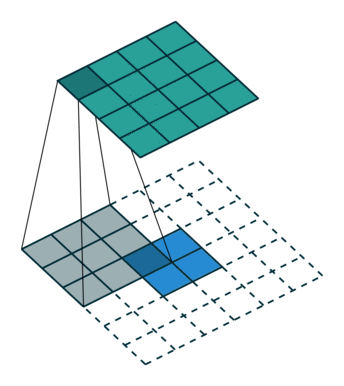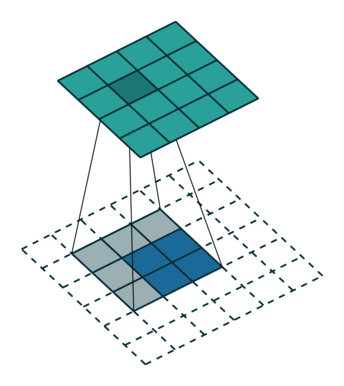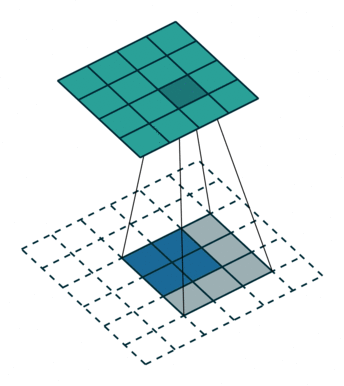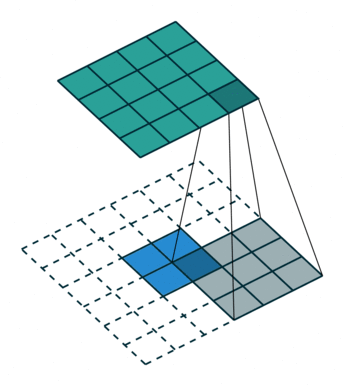 |
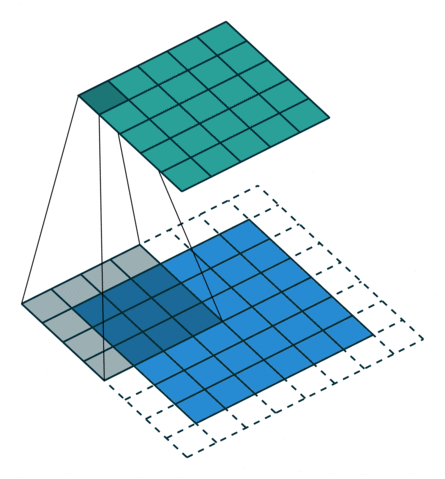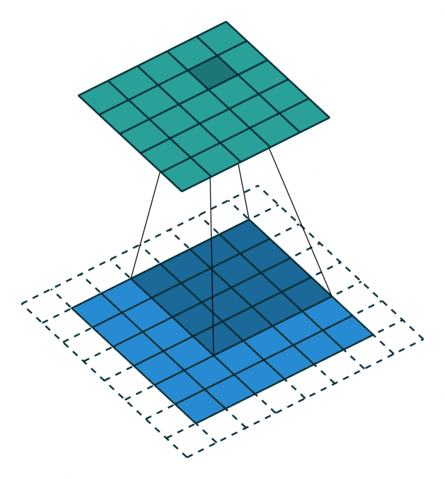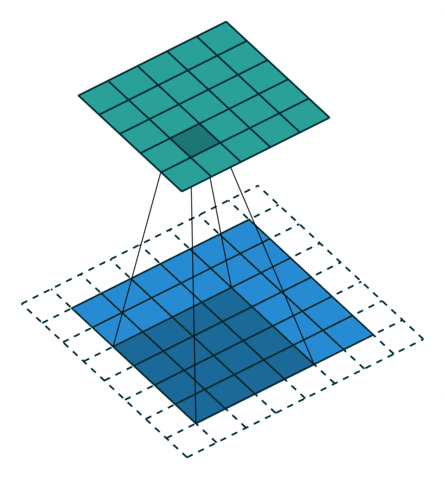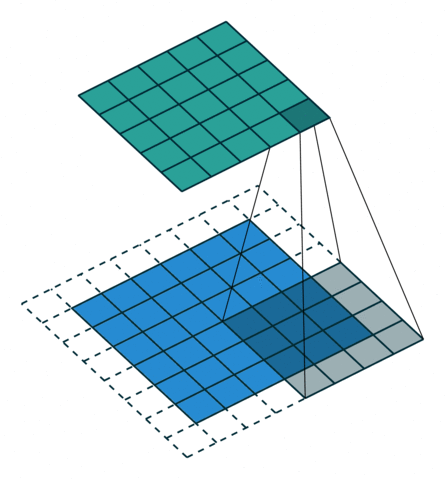 |
 |
 |
| No padding, no strides, transposed | Arbitrary padding, no strides, transposed | Half padding, no strides, transposed | Full padding, no strides, transposed |
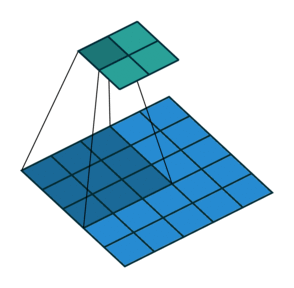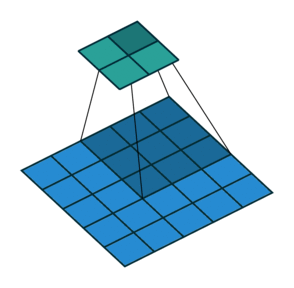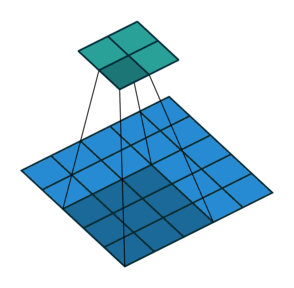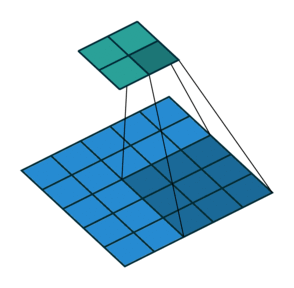 |
 |
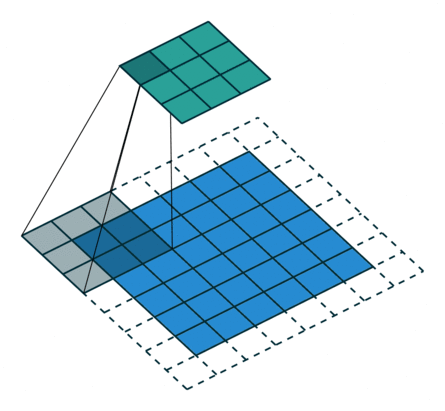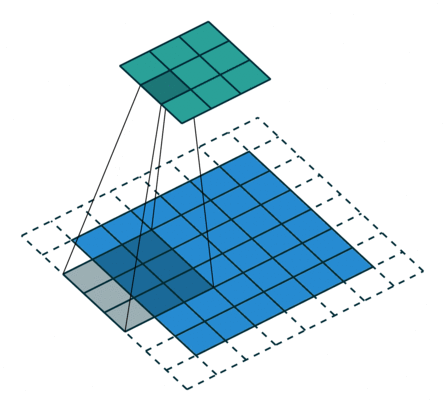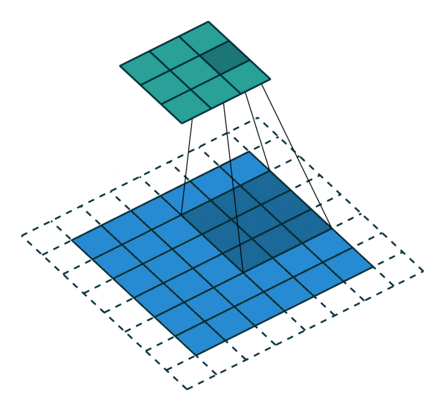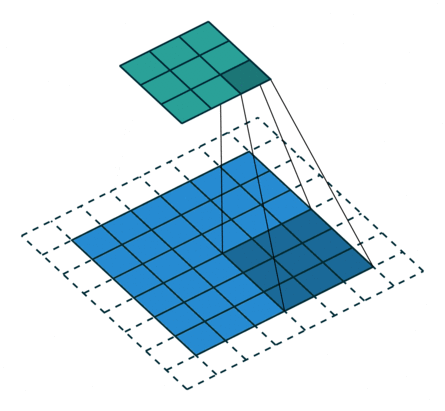 |
|
| No padding, strides | Padding, strides | Padding, strides (odd) | |
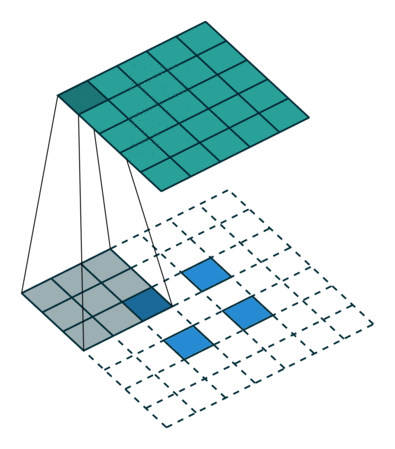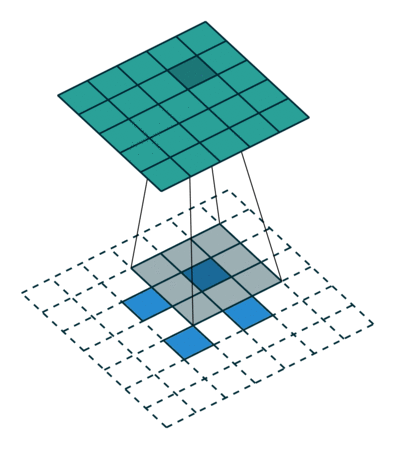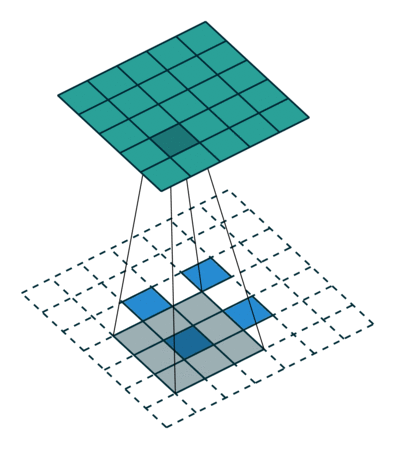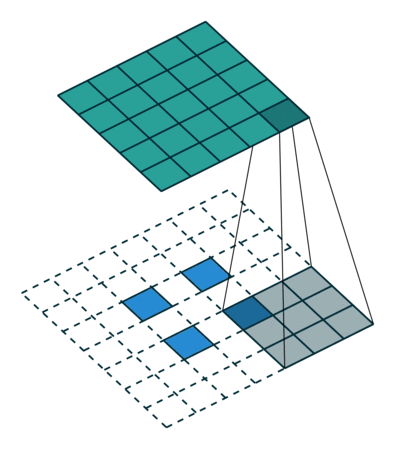 |
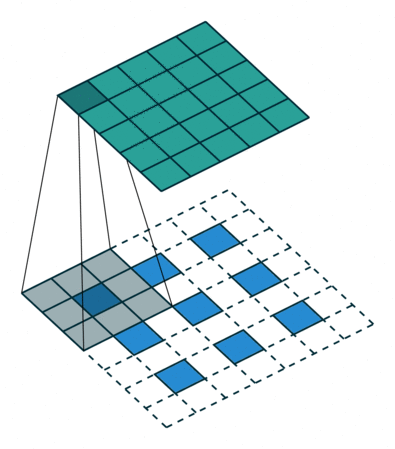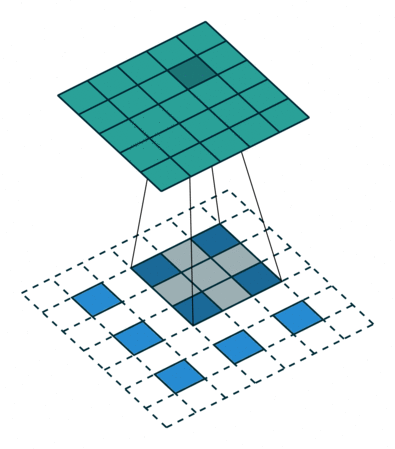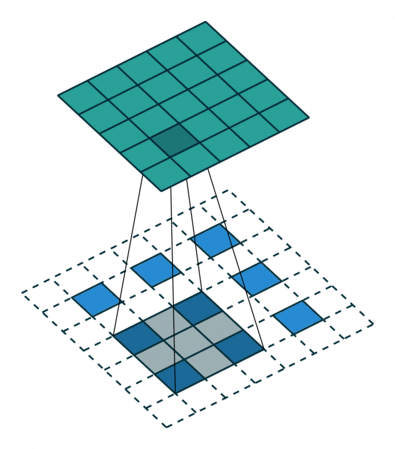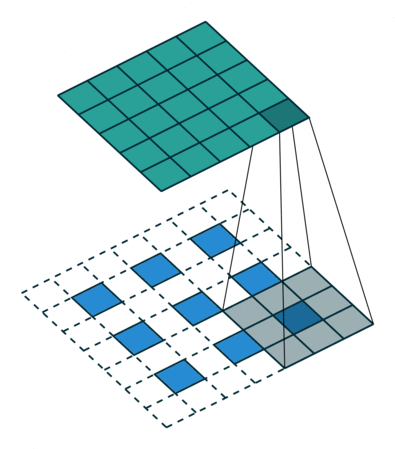 |
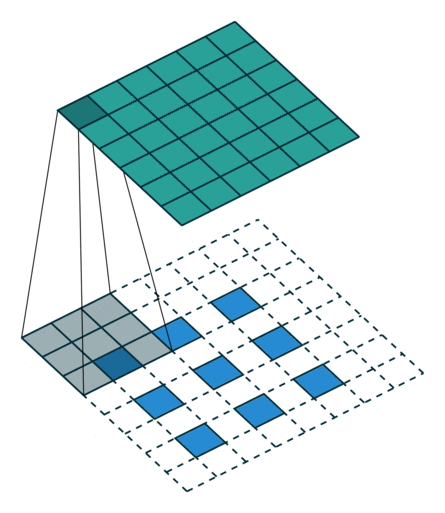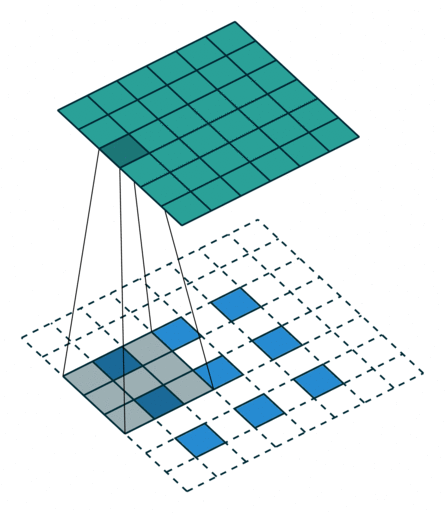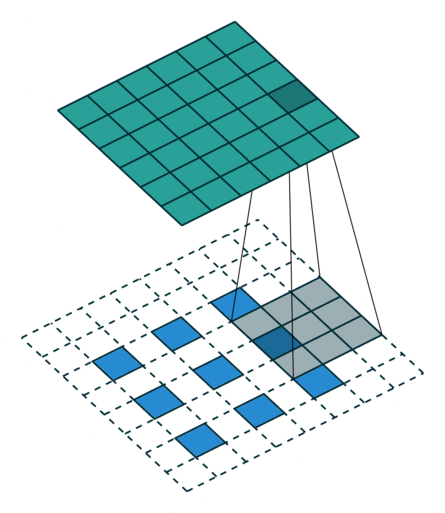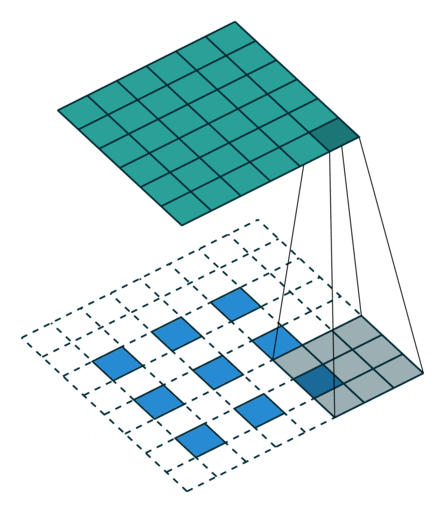 |
|
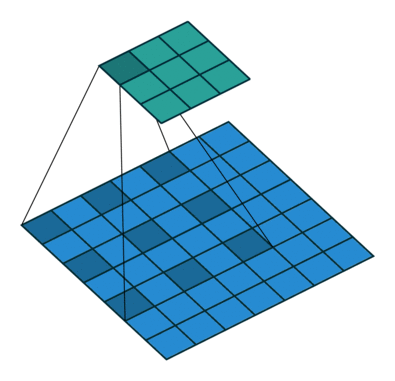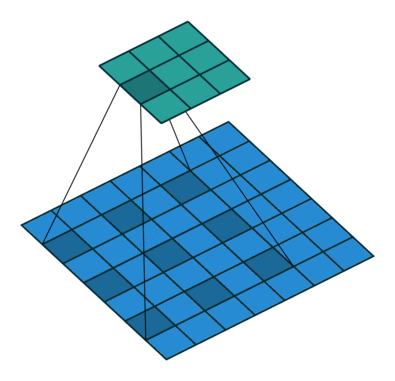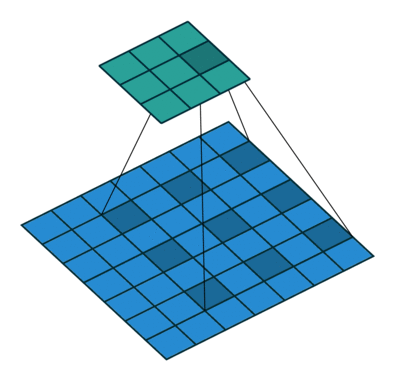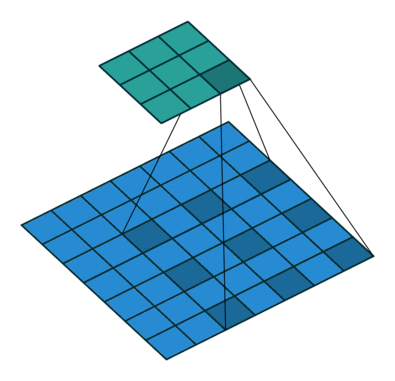
| No padding, strides, transposed | Padding, strides, transposed | Padding, strides, transposed (odd) | |
 |
|||
| No padding, no stride, dilation |
来源:https://github.com/vdumoulin/conv_arithmetic
形象解释各种卷积算法(Convolution animations)的更多相关文章
- Convolution卷积算法python以numpy,Matplotlib实现
1:简述 Numpy拥有函数numpy.convolve(a, v, mode='full')[source]¶,通过该函数完成卷积算法并图形化(Matplotlib)实现. 2:卷积定理 原理: 设 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 如何直观的解释back propagation算法?
转自:知乎-https://www.zhihu.com/question/27239198 作者:匿名用户链接:https://www.zhihu.com/question/27239198/answ ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 卷积神经网络中的Winograd快速卷积算法
目录 写在前面 问题定义 一个例子 F(2, 3) 1D winograd 1D to 2D,F(2, 3) to F(2x2, 3x3) 卷积神经网络中的Winograd 总结 参考 博客:blog ...
- 函数编程中functor和monad的形象解释
函数编程中functor和monad的形象解释 函数编程中Functor函子与Monad是比较难理解的概念,本文使用了形象的图片方式解释了这两个概念,容易理解与学习,分别使用Haskell和Swift ...
- 卷积(convolution)与相关(correlation)(matlab 实现)
1. 卷积(convolution) 输出 y(n) 是作为在 x(k) 和 h(n−k)(反转和移位)重叠之下的样本和求出的. 考虑下面两个序列: x(n)=[3,11,7,0,−1,4,2],−3 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 转置卷积Transposed Convolution
转置卷积Transposed Convolution 我们为卷积神经网络引入的层,包括卷积层和池层,通常会减小输入的宽度和高度,或者保持不变.然而,语义分割和生成对抗网络等应用程序需要预测每个像素的值 ...
随机推荐
- 11 个最佳的 Python 编译器和解释器
原作:Archie Mistry 翻译:豌豆花下猫@Python猫 原文:https://morioh.com/p/765b19f066a4 Python 是一门对初学者友好的编程语言,是一种多用途的 ...
- C++ | C++ 基础知识 | 类型与声明
一.类型 C++ 包含一整套基本类型,这些类型对应计算机最基本的存储单元并且展现 1.0 布尔值 一个布尔变量(bool)的取值或者是 true 或者是 false,布尔变量常用于表达逻辑运算结果. ...
- beetlex网关之聚合和url请求过虑
在这里主要介绍beetlex应用网关的两个插件,分别是聚合和url请求过虑.通过聚合插件可以把整合多个请求的数据来应答请求端,而Url请求过虑同可以拒绝一些有非常关键字的请求. 请求聚合 在网关服务中 ...
- C# WPF 嵌入网页版WebGL油田三维可视化监控
0x00 楔子 最近做的一个项目,是一个油田三维可视化监控的场景编辑和监控的系统,和三维组态有些类似,不过主要用于油田上. 效果如下图所示: 首先当然是上模型,设计人员跟进. 有了相关的模型,使用我们 ...
- kettle连接oracle数据库报错,ORA-12505
报错信息: Error connecting to database: (using class oracle.jdbc.driver.OracleDriver) Listener refused t ...
- python递归(函数)
递归:一个过程或函数调用自身的一种方法. 1. 效果图 2. 代码 def factorial(n): ''' 该函数用来求任意数的阶乘 参数: n 要求阶乘的数字 ''' # 基线条件 判断n是否为 ...
- 分享一款基于aui框架的图文发布界面
本文出自APICloud官方论坛, 感谢论坛版主 川哥哥 的分享. 分享一款基于aui框架的图文发布界面,可以添加多张图可以删除,类似qq空间发布说说,没做服务器后端,只演示前端操作.需要用到UIMe ...
- 继承Exception⭐⭐
public class ECOrderException : Exception { //第一种类型: throw new ECOrderException { ErrorCode = " ...
- C++数值计算
1.序 (1)程序设计分两种: 1.结构化设计(面向过程)——分解算法为模块,将算法的步骤分解为模块. 2.面向对象程序设计——主要是“类”与“对象”. (2)进制的转换 1.二进制转十进制 整数部分 ...
- Android栈溢出漏洞利用练习
在Github上看到一个Linux系统上的栈溢出漏洞利用练习项目: easy-linux-pwn.在原项目基础上,我稍微做了一些改动,将这个项目移植到了Android 9.0系统上: easy-and ...
