图像里的"白噪声"——电视机搜不到台时雪花斑点的形成原因

作者：❄️固态二氧化碳❄️ (主页)
链接：图像里的"白噪声"——电视机搜不到台时雪花斑点的形成原因 - 固态二氧化碳的博客 - CSDN博客
来源：CSDN博客
发表时间：2019年11月05日 18:14:07
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

  最近刚刚上了概率论与数理统计的课,了解了一些概率方面的知识,正好联想起了生活中的一个随机噪声问题,故写一篇文章来探讨一下这个问题。
  我们都知道在电视机搜不到台时,会出现杂乱无章,看起来十分不舒服的灰色雪花斑点,而在收音机搜不到台时,则会发出"沙沙"的噪声。而它们在原理上其实是一样的,都是由随机信号产生出来的效果。在搜不到台时,接收到的信号是杂乱无章的,类似于随机变量,而这些信号数字化后就类似于随机数序列。将随机数序列解码后,得到的声音/图像信息,正是"沙沙"的噪声和灰色雪花斑点。前者又称"白噪声",它是包含了所有频率信号的声音,且在各个频率处的功率谱密度均相等。我们知道,白光包含了所有频率的可见光,在各个频率处光功率相等,换句话说,白光就是由相等强度的所有颜色(频率)的可见光混合而成的。而随机噪声的频谱分布正好符合白光的特点,因此得名"白噪声"。
  电视机的灰色雪花斑点,原理上和白噪声是相同的,都是随机信号产生的噪声,所以这雪花斑点也属于一种"白噪声",不过这是图像上的白噪声,但为了简化,在下文中我将其简称为"白噪声"。
  (关于声音中的白噪声,由于我还没有了解关于信号与声音方面的知识,所以在这篇文章中我不会做相关介绍,不过我在以后的文章中还是会写的)

  另外附上一个在网上流传的比较常见的一种错误说法,就是说白噪声和雪花背景来自于所谓的宇宙"微波背景辐射",其实这种说法完全是错误的,希望大家不要以讹传讹。
  白噪声和雪花背景的确是随机信号辐射引起的,但来源肯定不是宇宙背景辐射。因为宇宙空间离地面相当远,而本身微波背景辐射是非常微弱的,强度相当小,这些辐射经过大气层后会衰减很多,而且地球周围其他信号的干扰会使得探测背景辐射愈发困难。在其他信号面前,这一点辐射可以说是九牛一毛,微不足道,完全可以忽略不计。所以"宇宙背景辐射说"是完全站不住脚的。
  这些信号真正的来源是电视机周围空间中的混杂的其他干扰信号,以及电视机自身磁场产生的信号,这些充斥在电视机周围的无序随机信号才是导致白噪声和雪花信号的形成的根本原因。在具体分析之前,我必须先澄清这一点。

  进入正题。电视机无台时的灰色斑点是随机的图像信号,那么我们生成一个随机的位图文件,得到的就是这样的图案。现在我们用Winhex软件生成一段随机序列,并且放入BMP文件的数据段内。BMP文件由文件头和数据段组成,文件头包括图像的长宽,色深等信息,数据段则记录着每个像素的颜色。

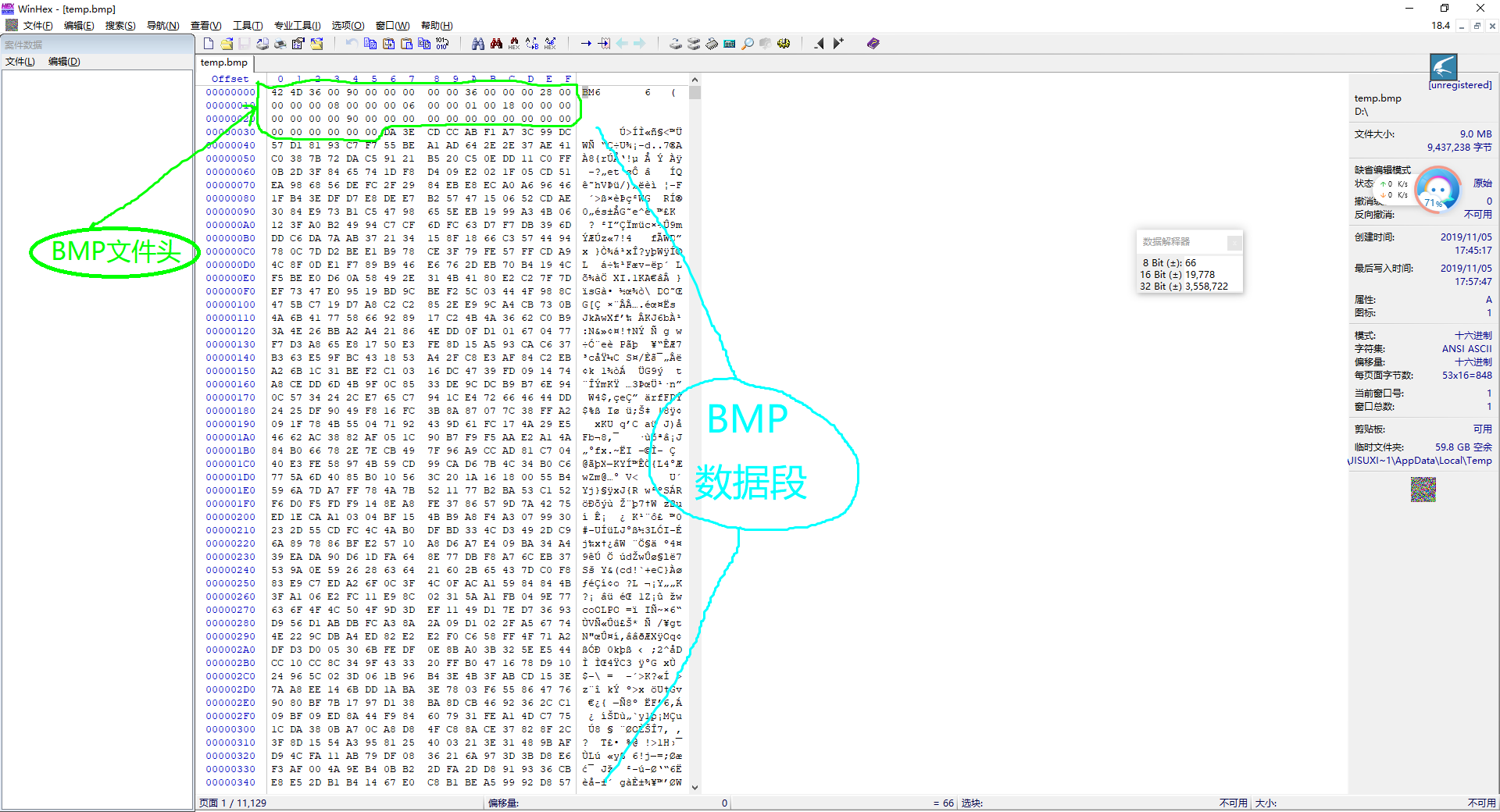
BMP文件结构

  这是一个2048×1536的随机图像,文件头表示图像尺寸为2048×1536,数据段则为WinHEX生成的随机序列,生成方法如下:

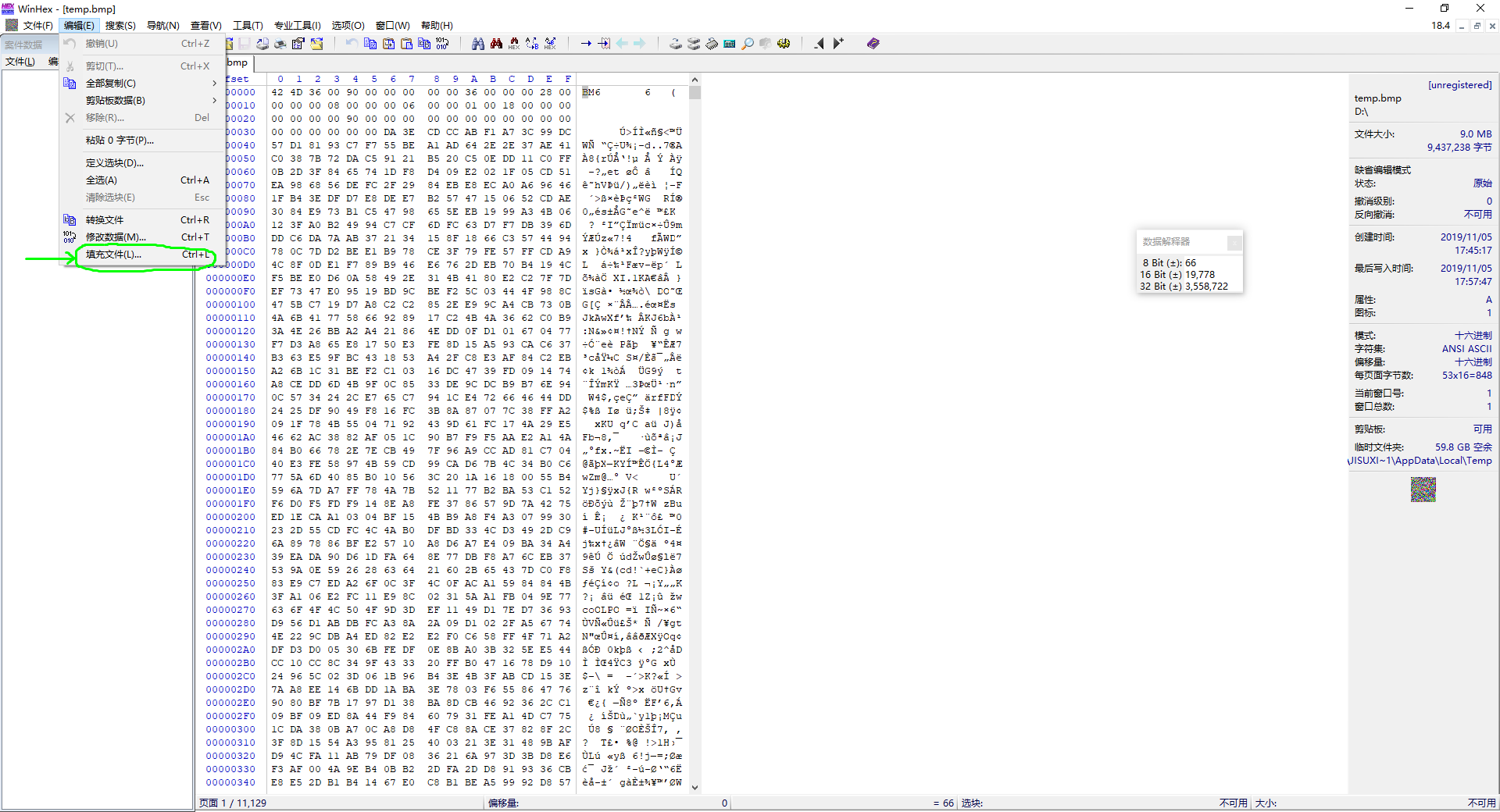
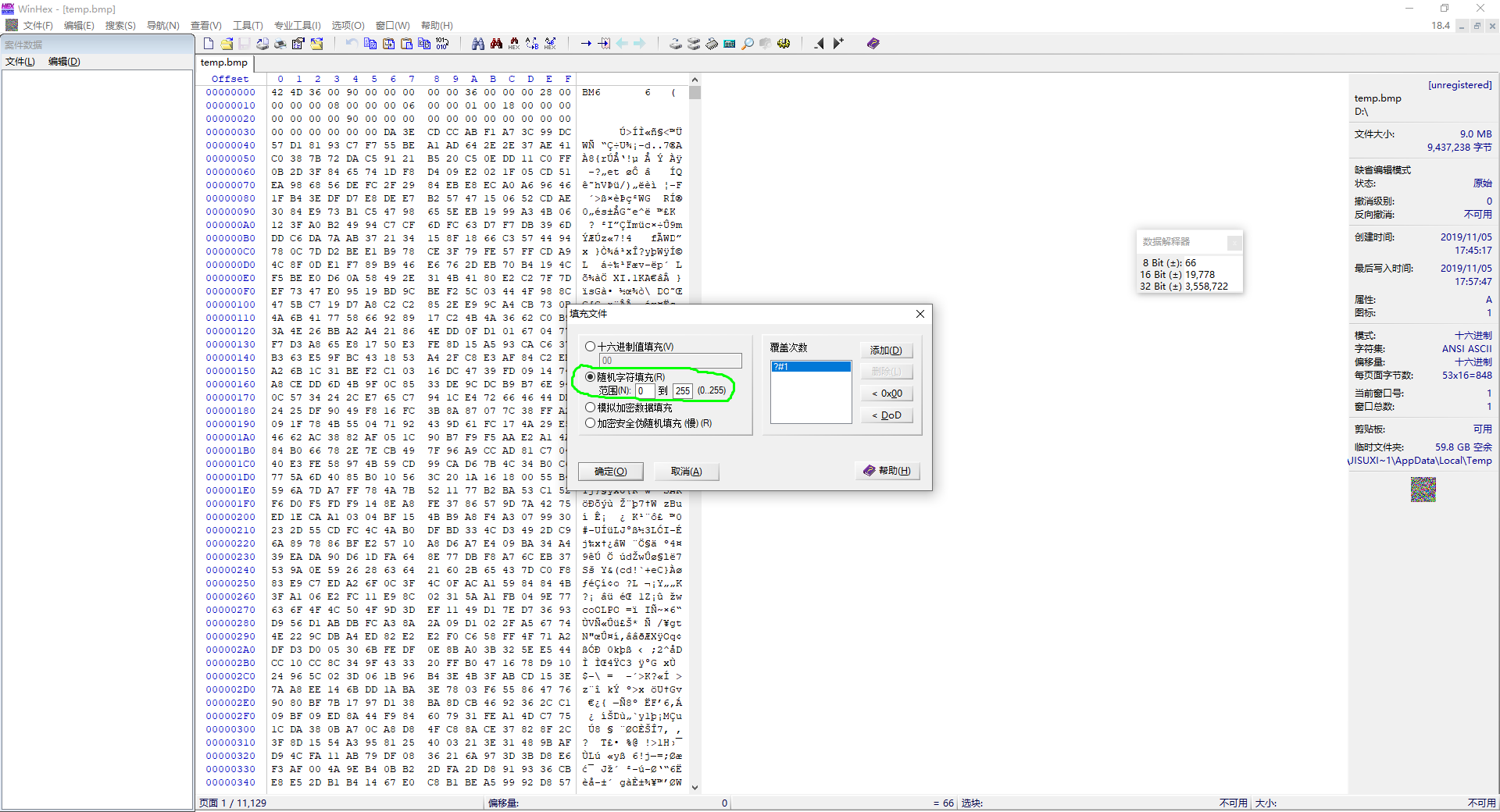
  生成效果如下:

  这就很像电视机无台时的灰色斑点了。但是,这种灰色究竟是怎么样的一种灰色呢?这里就需要用到概率论的知识了。
  我们都知道,电子图像是用RGB表示的,用RGB三个通道的值,来表示RGB三种颜色的深浅程度。利用不同深浅的三种颜色,就可以合成出各种不同的"彩色"(这里的"彩色"实际上是利用了人眼不能区分同色异谱的光的特点,用三种颜色合成出的"彩色",达到欺骗人眼的目的,同时也节省了显示器的成本。如果我们不这样做,那么图像就得像声音一样,需要使用不同频率的光,进行振动波形描述来表示,这样显然增加了显示器的硬件制造成本,同时也增加了图像的存储体积,造成了空间浪费,显得很不经济划算。所以我们能用RGB合成出各种色彩,其实只是利用了人眼视觉上的弱点,投机取了个巧罢了)。而雪花斑点本质上是随机图像,图像中RGB三个通道的值均为随机数,所以RGB三个通道的地位其实是平等的,平均下来的值(数学期望)也是相等的,因此图像会呈现出灰色。但是,这种灰色的灰度值到底是多少呢?下面我们就要进行计算。
  在进行计算之前,我们首先需要了解gamma值的概念。因为电脑图像所存储的灰度值与实际的亮度并不成正比,不能直接进行加和,否则会得到错误的结果。
  电脑图像中所存储的灰度值,有时又被称为"亮度",实际上是心理亮度。比如说(127.5,127.5,127.5)的灰色,在心理感知上的亮度,是(255,255,255)的白色的一半。但是实际上的物理功率并非是一半,而是\((\frac{1}{2})^{2.2}≈0.21763764\)倍,这是怎么回事呢?
  原来,物理亮度由功率决定,与功率成正比,而人眼对亮度的感知与功率并不成正比,而是幂函数的关系,这个函数的指数我们通常称作伽马(gamma)值,符号为γ。如果我们把物理亮度(相对功率)记为\(L_p\),心理亮度(计算机图像中存储的值)记为\(L\),则有\(L_p=L^γ\)。对于人眼而言,这个伽马值通常在1.8~2.6之间,而在绝大多数电脑上,这个值取的是2.2,所以我们有\(L_p=L^{2.2}\)。
  而颜色的加和是物理亮度的相加,并非心理亮度,所以RGB颜色值不能直接相加,如果这样做就是无意义的,会计算出错误的值。所以我们先要将RGB通道的值换算成物理亮度,然后再进行计算。但是最后计算得到的值又要换算成心理亮度,才能变成RGB通道的值,存储在图像中。因此实际上我们要进行两步换算后才能得到最终的值。

  我们知道,随机图像的RGB三个通道的值均为随机数。为了计算方便,我们先将其进行归一化,换算成0~1之间的值,这样RGB三个通道的值就都服从0~1区间上的均匀分布。由于RGB三个通道在这里的地位是平等的,所以我们只取其中的一个值进行分析,将其记为随机变量\(X\),则\(X\sim U(0,1)\)。
  将\(X\)对应的物理亮度记为\(Y\),则\(Y=X^{2.2}\)。
  我们看到的雪花斑点图像的最终效果,其实是许多像素颜色值的平均值(数学期望),像素越多,偏差程度(方差)越小(大数定律),看起来灰色越均匀。前面我们说过,颜色的加和是按照物理亮度计算的,亮度的平均值,也就是单位面积上的亮度,是先将一定面积的像素亮度进行加和,再除以总面积。这个过程需要用到加法运算,所以我们只能对物理亮度进行这样的运算,也就是求物理亮度\(Y\)的数学期望\(E(Y)\),然后再换算成计算机图像里的灰度值。
  设随机变量\(X\)具有概率密度\(f_X(x)\),\(m<x<n\),函数\(g(x)\)在\((m,n)\)可导且在\((m,n)\)恒有\(g'(x)>0\)(或\(g'(x)<0\)),则\(Y=g(X)\)是连续型随机变量,其概率密度为
\[
f_Y(y)=\left\{\begin{aligned}
& f_X[h(y)]|h'(y)| & (α<y<β) \\
& 0 & (其他)
\end{aligned}\right.
\]

  其中\(α=min[g(m),g(n)]\),\(β=max[g(m),g(n)]\),\(h(y)\)是\(g(x)\)的反函数。

  在这里,\(Y=X^{2.2}\),\(g(x)=x^{2.2}\),\(h(y)=y^{\frac{1}{2.2}}\),\(h'(y)=\frac{1}{2.2}y^{-\frac{1.2}{2.2}}\)。
  由于\(X\sim U(0,1)\),故
\[
f_X(x)=\left\{\begin{aligned}
& 1 & (0<x<1) \\
& 0 & (其他)
\end{aligned}\right.
\]
  所以
\[
f_Y(y)=\left\{
\begin{aligned}
& f_X(y^{\frac{1}{2.2}})|\frac{1}{2.2}y^{-\frac{1.2}{2.2}}| & (0<y<1) \\
& 0 & (其他)
\end{aligned}
\right.
%
=\left\{
\begin{aligned}
& \frac{1}{2.2}y^{-\frac{1.2}{2.2}} & (0<y<1) \\
& 0 & (其他)
\end{aligned}
\right.
\]

  \(Y\)的数学期望\(E(Y)=\int_{0}^{1}y·\frac{1}{2.2}y^{-\frac{1.2}{2.2}}\mathrm{dy}=\int_{0}^{1}\frac{1}{2.2}y^{\frac{1}{2.2}}\mathrm{dy}=[\frac{1}{2.2}·\frac{2.2}{3.2}y^{\frac{3.2}{2.2}}]_0^1=[\frac{1}{3.2}y^{\frac{3.2}{2.2}}]_0^1=\frac{1}{3.2}\)
  即物理亮度的平均值为\(\frac{1}{3.2}\),换算成RGB通道值(归一化)为\(\sqrt[2.2]{\frac{1}{3.2}}≈0.58936776\),则实际存储RGB值为\(255\sqrt[2.2]{\frac{1}{3.2}}≈150.288778\),四舍五入为\(150\)。因此我们得出结论,电视机搜不到台时灰色雪花斑点对应的灰色值为(150,150,150),即#969696。下面我们来对比一下雪花斑点图像以及(150,150,150)灰色纯色图像,看看他们是否相近。

  两者看上去已经比较接近了,但是前面一幅图更加杂乱。事实上在同样大小的区域里,如果把前面一幅图像素做得足够多,密度足够大,肉眼看上去就和后面一幅几乎没有区别了。原因是像素数增多,根据大数定律,其颜色的平均值的数学期望不变,而方差会减小,即整体偏离程度减小,整幅图看起来就更加均匀,杂点占比更小,更接近于纯色的灰色。

作者：❄️固态二氧化碳❄️ (主页)
链接：图像里的"白噪声"——电视机搜不到台时雪花斑点的形成原因 - 固态二氧化碳的博客 - CSDN博客
来源：CSDN博客
发表时间：2019年11月05日 18:14:07
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。