神经网络损失函数中的正则化项L1和L2

神经网络中损失函数后一般会加一个额外的正则项L1或L2,也成为L1范数和L2范数。正则项可以看做是损失函数的惩罚项，用来对损失函数中的系数做一些限制。

正则化描述：

L1正则化是指权值向量w中各个元素的绝对值之和;

L2正则化是指权值向量w中各个元素的平方和然后再求平方根;

一般都会在正则化项之前添加一个系数，这个系数需要用户设定，系数越大，正则化作用越明显。

正则化作用：

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择，一定程度上，L1也可以防止过拟合;
L2正则化可以防止模型过拟合（overfitting）;

何为稀疏矩阵

稀疏矩阵指的是很多元素为0，只有少数元素是非零值的矩阵。

神经网络中输入的特征数量是庞大的，如何选取有效的特征进行分类是神经网络的重要任务之一，如果神经网络是一个稀疏模型，表示只有少数有效的特征（系数非0）可以通过网络，绝大多数特征会被滤除（系数为0），这些被滤除的特征就是对模型没有贡献的“无关”特征，而少数系数是非0值的特征是我们需要额外关注的有效特征。也就是说，稀疏矩阵可以用于特征选择。

L1正则化是怎么做到产生稀疏模型的？

假设有如下带L1正则化的损失函数：

Loss = Loss_0 + αL1

Loss_0是原始损失函数，L1是加的正则化项，α 是正则化系数，其中 L1 是 模型中权重 w 的绝对值之和。

神经网络训练的目标就是通过随机梯度下降等方法找到损失函数 Loss的最小值，加了L1之后，相当于对原始Loss_0做了一个约束，即在 L1 约束下求Loss_0最小值的解。

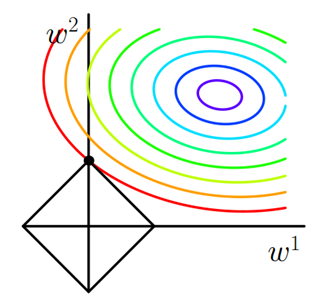
对于最简单的情况，假设模型中只有两个权值 w1 和 w2 ，对于梯度下降法，可以分别画出求解 Loss_0 和 L1 过程中的等值线，如下图：

等值线是说在等值线上任一点处（取不同的w1和w2组合），模型计算的结果都是一样的。

图中彩色弧线是Loss_0的等值线，黑色方框是 L1的等值线。在图中，当Loss_0等值线与L1图形首次相交的地方就是一个最优解，这个相交的点刚好是L1的顶点。

注意到L1函数有很多个突出的点，二维情况下有4个，维数越多顶点越多，这些突出的点会比线段上的点有更大的几率首先接触到 Loss_0的等值线，而这些顶点正好对应有很多权值为0的矩阵， 即稀疏矩阵，这也就是为什么L1正则化可以用来产生稀疏矩阵进而用来进行特征选择的原因。

对于L1正则化前的系数α，是用来控制L1图形的大小，α越大，L1中各个系数就相对越小（因为优化目标之一是α×L1的值趋近于0。α大，L1系数取值就会小），L1的图形就越小; α越小，L1中各个系数就相对越大，L1的图形就越大。
L2正则化是怎么做到防止模型过拟合的？

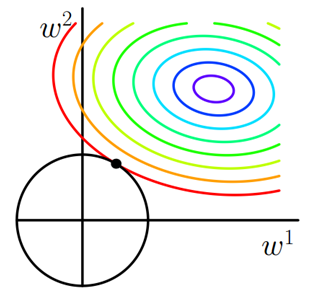
仍以最简单的模型，只有两个权重w1 和 w2为例，Loss_0和L2分别对应的等值线形状如下图：

由于L2是w1和w2平方和再开方，所以L2的图形是一个圆。圆形相对方形来说没有顶点，Loss_0 和 L2图形相交使得 w1或者w2等于的概率大大减小，所以L2正则化项不适合产生稀疏矩阵，不适合用来选择特征。

相对来说，模型中所有矩阵系数都比较小的模型具有更强的抗干扰能力，也就是说可以避免过拟合。对于这种小系数的模型，特征会乘以很小的系数，使得特征的波动被压缩，所以泛化能力更好。

L2正则化项的公式是所有权重系数平方之后再开方，所以在每次迭代过程中， 都会使得权重系数在满足最小化Loss_0的基础上，一步一步使得权重系数w1和w2趋向于0，最终得到权重系数很小的矩阵模型，达到防止过拟合的作用。

对于L1正则化项，如果α系数取很大，也会得到系数极小的最优解，这时的L1也具有防止过拟合的作用。

L1和L2中的α系数的作用是类似的，α系数越大，正则化作用越明显（但同时也可能意味着模型越难以收敛），从等值图上直观看就是L图形越小，对应矩阵系数越小。